Лекция оптимизации потоков в сетевой постановке

Условия транспортной задачи в матричной постановке предполагают, что все пункты делятся на две категории – отправления и назначения (производства и потребления), что каждый пункт потребления связан с каждым пунктом производства единственным маршрутом, а пункты одной категории не связаны между собой маршрутами.

Однако во многих практических задачах ситуация оказывается более сложной. Это относится прежде всего к задачам о реальных перевозках на железнодорожном или автомобильном транспорте, когда имеется сложная сеть коммуникаций, в узлах которой расположены пункты производства, потребления и так называемые перевалочные пункты, т.е. пункты, в которых нет ни производства, ни потребления, но через которые транзитом перевозится продукт. Последнее обстоятельство объясняется тем, что не всегда можно попасть непосредственно из любого пункта производства в любой пункт потребления, минуя промежуточные пункты. Другими словами, маршрут следования продукции из пункта производства в пункт назначения может состоять из последовательности коммуникаций, каждая из которых соединяет два "соседних пункта", причем таких маршрутов для заданного пункта производства и заданного пункта потребления может быть несколько.

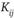В соответствии со сказанным введем понятие транспортной сети. Под транспортной сетью будем понимать совокупность пунктов (), некоторые из которых соединены направленными отрезками (коммуникациями) . Если существует коммуникация ., идущая от пункта к пункту 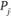, то это означает, что из пункта 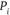в пункт 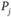могут осуществляться перевозки продукта. Подчеркнем, что наличие коммуникации означает возможность только одностороннего движения.

В тех случаях, когда в действительности допустимы перевозки в обоих направлениях между пунктами и , эти два пункта должны быть соединены парой коммуникаций противоположного направления ().

Каждый пункт транспортной сети должен быть охарактеризован числом – объемом производства. В зависимости от знака этой величины все пункты делятся на пункты производства, пункты потребления и перевалочные пункты. Для пунктов производства числа должны быть положительными, для пунктов потребления – отрицательными (противоположное объему производства число означает объем потребления). Для перевалочных пунктов объем производства полагается равным нулю.

Каждой коммуникации следует приписать два числа – пропускную способность и стоимость перевозки. Первое из них () показывает, какое максимальное количество единиц продукта может быть перевезено по этой коммуникации, а второе (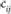) определяет стоимость перевозки одной единицы продукта из пункта 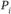в пункт 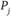по коммуникации .

Пример транспортной сети изображен на рис. 4.7. Здесь имеется 10 пунктов 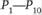. Положительные и отрицательные числа, проставленные в изображениях этих пунктов, означают объемы производства.

Пункты – пункты производства с объемами производства соответственно 30, 70, 50 единиц; пункты 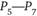– пункты потребления с объемами потребления, равными соответственно 60, 40, 50 единиц; пункты , 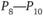– перевалочные пункты (отсутствие в соответствующих кружочках объемов производства означает, что они равны нулю).

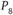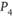Направленные отрезки, соединяющие некоторые пункты, изображают коммуникации. Так, из пункта в пункт продукт может перевозиться по коммуникации . В то же время из пункта в пункт или в пункт непосредственно, минуя промежуточные пункты, продукт перевозиться не может, ибо коммуникации и отсутствуют. В то же время между пунктами и 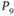перевозки могут осуществляться непосредственно в обе стороны, ибо эти пункты соединены парой коммуникаций и 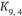. Пропускные способности коммуникаций представлены знаменателями дробей, стоящих у каждой коммуникации, а стоимости перевозок – числителями этих дробей.

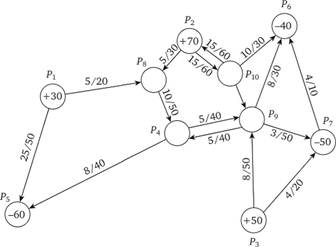
Рис. 4.7. Пример транспортной сети

Если задана транспортная сеть, то возникает задача организации перевозок по коммуникациям этой сети. Число единиц продукта, перевозимое по коммуникации из пункта в пункт , обозначим через , поскольку мы условились рассматривать лишь коммуникации с односторонним движением, 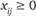. Учет пропускной способности приводит к дополнительному требованию . Совокупность чисел , удовлетворяющих условиям

(4.21)

определяет некоторую систему перевозок по всем коммуникациям транспортной сети. Однако эта система, вообще говоря,

не согласуется с объемами производства и потребления пунктов сети.

Количество единиц продукта, вывозимого из произвольного пункта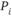в соответствии с системой перевозок 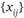, равно , где – множество номеров тех пунктов, в которые из пункта идут коммуникации. Точно так же количество единиц продукта, ввозимого в пункт 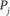, определяется выражением , где – множество номеров пунктов, из которых в пункт идут коммуникации. Таким образом, разница между количеством вывозимого и количеством ввозимого продукта для пункта равна

Для того чтобы система перевозок 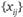согласовалась с объемами производства и потребления, необходимо, чтобы эта разница для каждого пункта была равна объему производства в этом пункте.

Отсюда приходим к следующему определению плана транспортной задачи на сети: планом называется любая совокупность чисел , удовлетворяющая условиям

(4.22)

Легко подсчитать общую стоимость перевозок, определяемых планом :

(4.23)

где суммирование ведется по всем коммуникациям транспортной сети.

Транспортная задача в сетевой постановке заключается в отыскании плана перевозок с наименьшей стоимостью. Другими словами, она состоит в нахождении минимума линейной функции (4.23) при условиях, накладываемых на неизвестные, заданных системой линейных равенств и неравенств (4.22).

Можно показать, что любая транспортная задача в сетевой постановке может быть сведена к транспортной задаче в матричной постановке с ограниченными пропускными способностями. Однако такой подход оказывается нерациональным, так как разработаны специальные методы решения, непосредственно учитывающие специфику сетевой постановки и потому значительно более простые [11].