Как определить цену опциона
Другой важный аспект развития анализа риска появился в 1973 г. после публикации двух работ по ценообразованию опционов Фишера Блэка, Майрона Шоулза и Роберта Мертона[1]. На момент публикации их основополагающей работы профессора Блэк и Шоулз работали в университете Чикаго, а Мертон был профессором в MIT[2]. В 1998 г. Мертон и Шоулз удостоились Нобелевской премии. (Блэк умер в 1995 г.)
Опционы – это финансовые активы, которые дают право своим владельцам приобрести или продать другой актив в заранее оговоренную дату по заранее согласованной цене, называемой ценой исполнения. Опцион на покупку актива называется колл, а опцион на продажу актива называется пут. (См. также гл. 6.)
Цена, выплаченная за опцион колл, – это обычно часть текущей цены базового актива, на который подписан опцион (контракт). Остаток выплачивается в дату исполнения опциона в некоторый момент в будущем. Следовательно, одно из преимуществ покупки опциона колл – это возможность покупки актива в кредит.
На момент исполнения покупатель сохраняет за собой право отказаться от своего намерения исполнить контракт. Таким образом, если цена актива на момент исполнения ниже, чем цена, установленная по опционному контракту, покупатель опциона колл может выбрать вариант неисполнения контракта. В сущности, опцион колл предлагает некую форму страхования цены.
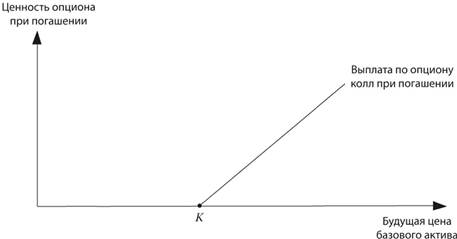
Рисунок 5-4 описывает денежный поток от опциона колл при погашении (т.е. когда истекает срок контракта). Опцион имеет нулевой денежной поток при погашении, поскольку цена базового инструмента ниже цены исполнения (цены реализации) К. Для цены выше цены исполнения владелец опциона колл имеет право на разницу между ценой базового инструмента и ценой исполнения. Этот последний денежный поток представлен наклонной кривой, возрастающей при движении вправо от точки К при повышении цены базового актива.
РИСУНОК 5-4. Выплата по опциону колл при погашении
Для опциона пут имеет место обратное. Покупатель платит за право продать акцию в будущем по заранее оговоренной цепе. Эта цена исполнения составляет гарантированную минимальную цену. С другой стороны, если рыночная цена актива выше, чем цена, которую покупатель опциона пут получит при исполнении опциона пут, он может игнорировать опционный контракт и выбрать вместо этого продажу актива на отрытом рынке за полную стоимость. Таким образом, опцион пут, которым владеют с базовым активом, обеспечивает страховку против снижения стоимости базового актива ниже цены исполнения.
В публикации 1973 г. Блэк и Шоулз (в литературе часто используется сокращение B&S) разработали классическую модель ценообразования опционов. Мертон, который сотрудничал с B&S, также опубликовал важную работ}' в 1973 г., предлагая альтернативный способ доказательства модели оценки и множества ее дополнительных расширений. Кроме того, в дополнение к расчету равновесных рыночных цен для обращающихся на рынке опционов данная модель определяет различные компоненты опциона и взаимосвязи между ними.
Например, как мы уже обсуждали, опцион колл можно охарактеризовать как "пакетную сделку", которая включает:
■ покупку акции (или другого актива);
■ взятие кредита;
■ покупку страховки.
Можно показать, что за совсем небольшой интервал времени опцион колл можно разложить на покупку определенной пропорции базового инструмента (данная пропорция называется "дельта" опциона) и взятие кредита (сумма кредита пропорциональна вероятности того, что опцион будет исполнен). Теория опционов оказалась бесценной для управления портфелем и управления рисками. Используя данные идеи, портфельные менеджеры могут динамически корректировать инвестиционные позиции с целью отражения изменяющихся ожиданий, рыночной конъюнктуры и потребностей клиента. Покупка опциона пут к активам, находящимся в портфеле, – это то же самое, что и страхование этих активов. Покупка и продажа комбинации опционов колл и пут помогает инвесторам маневрировать в волатильных или неустойчивых рынках. (См. обсуждение опционов на снижение рисков в гл. 6.)
Подробные математические выкладки, которые содержатся в модели B&S, довольно сложны для расчета без помощи компьютерных технологий. Но функции, которые управляют ценой опциона, достаточно наглядны. Проще говоря, цена опциона – это функция:
■ цены базового актива;
■ цены исполнения (страйк), указанной в контракте;
■ преобладающей безрисковой ставки;
■ волатильности базового актива;
■ времени, оставшегося до заранее оговоренной даты исполнения.
Если цена акции повышается и все остальные параметры остаются постоянными величинами, то ценность опциона колл повышается. Аналогичным образом, если цена исполнения снижается или увеличивается срок погашения, то стоимость (ценность) опциона колл возрастает. По мере того как базовый актив становится более волатильным, стоимость (ценность) опциона колл повышается. Причина в том, что опцион колл не подвержен риску снижения стоимости, т.е. не имеет значения, насколько опцион колл "вне денег" (out-of-the-money) при истечении его срока, его стоимость (ценность) все равно будет равна нулю, в то время как повышение уровня волатильности повышает вероятность того, что опцион при погашении будет "в деньгах" (in-the-money), т.е. вероятно, что цена акции будет иметь более высокое значение. Кроме того, при повышении процентных ставок стоимость (ценность) опциона колл также возрастает (так как приведенная ценность выплаты при исполнении уменьшается при повышении процентных ставок). Подобные же аргументы используются и для опционов пут, хотя чувствительность опционов пут к ряду факторов противоположна.
Из этих всех факторов наиболее существенным для оценки рисков и управления ими с помощью опциона является волатильность базового актива. Часто говорят, что опционы "дружелюбны для риска": повышение волатильности (т.е. повышение уровня риска) базового актива, при условии, что все остальные параметры имеют постоянные значения, приводит к повышению цены опциона колл и пут. Как вы помните, волатильность измеряется среднеквадратическим отклонением (корень квадратный из дисперсии) ставки доходности базового актива на протяжении некоторого выбранного исторического периода.
При использовании исторических данных для расчета будущего уровня волатильности, мы делаем сомнительное допущение: волатильность с течением времени остается постоянной. При ликвидном рынке опционов, однако, модель B&S предлагает еще один вариант решения проблемы. Помните, что модель B&S предлагает оценивать опционы, учитывая, что мы имеем доступ к вводимым данным, приведенным ранее. С другой стороны, если мы уже имеем цену опциона на ликвидном рынке опционов, то мы можем использовать эту "выходную" информацию в качестве одного из вводимых данных. Тогда формула может быть использована для расчета недостающих данных, например волатильности. В действительности, по формуле B&S, таким образом, можно рассчитать волатильность, подразумеваемую ценами опционов на рынке. Поэтому эта величина часто просто называется подразумеваемой волатильностью.
Подразумеваемая волатильность имеет огромное практическое значение для тех, кто постоянно торгует опционами на рынке, и они часто повторно вводят данные в модель B&S для расчета цены нескольких различных серий опционов с различными ценами исполнения и сроками погашения. Но так как подразумеваемая волатильность не является непосредственно наблюдаемой и зависит от модели, в прошлом возникало некоторое ее влияние на управление операционным риском отделений по работе с рисками. Трейдер, который оценивает позиции по опционам для управления рисками с использованием величины подразумеваемой волатильности, которую он или она рассчитал на основании рыночных данных, может столкнуться с сильным искушением. В прошлом трейдеры определенных инвестиционных банков умышленно вносили неверные данные подразумеваемой волатильности, чтобы изменить видимую стоимость их "скрытого" портфеля опционов. Подразумеваемую волатильность вызывает особенное беспокойство, так как это единственные данные в модели B&S, которые аудиторам невозможно проверить без наличия определенного рода специализированных знаний. Это один из примеров того, как вопросы, связанные с принципами моделирования рисков, влияют на практику управления рисками. К этой теме мы вернемся в гл. 14.
Модель B&S также дает понимание того, как опционы, представленные в портфеле финансовых активов, взаимодействуют с другими активами и влияют на общий риск портфеля. Систематический риск (бета) опциона колл или пут – это величина, равная бете базового актива, умноженной на эластичность опциона колл или пут. Под эластичностью мы понимаем процентное изменение ценности опциона при изменении на 1 % цены базового актива. Из модели следует, что эластичность опциона колл положительна, больше или равна единице, а эластичность опциона пут меньше или равна нулю. Следовательно, пополнение портфеля опционом колл будет повышать общий уровень риска портфеля (для положительного коэффициента бета), в то время как опционы пут снижают риск портфеля. Короткая позиция по опционам колл, т.е. продажа опциона колл, также может снижать уровень риска портфеля, так как такая позиция имеет отрицательный коэффициент бета.
Модель B&S также можно использовать для расчета коэффициента хеджирования позиции по опциону, также известного как коэффициент дельта. Этот коэффициент описывает изменение ценности опциона в результате незначительного изменения цены базового актива. Коэффициент хеджирования показывает то, каким образом риск финансового актива можно хеджировать опционами. Цена как базового актива, так и опционов изменяется с течением времени, поэтому коэффициент хеджирования по сути дела динамичен и требует корректировки портфеля для поддержания целевого уровня хеджирования. Коэффициент хеджирования опциона колл колеблется от 0 до 1, а дельта опциона пут – от -1 до 0.
Например, представим, что дельта опциона колл, который немного вне денег, равна 0,5, что означает, что если цена базовой акции повысится (снизится) на 1 долл., то стоимость опциона колл повысится (снизится) на 0,50 долл. Это означает, что если мы хотим нейтрализовать на краткосрочном временно́м горизонте риск длинной позиции но опционному контракту колл на 100 акций, мы должны продать 50 акций.
Выводы модели, представленной Блэком и Шоулзом в 1970-х гг., привели к дальнейшим исследованиям в области финансов, в частности в отношении волатильности, например за последние два десятилетия в качестве реакции на то, что волатильность на финансовых рынках может значительно изменяться с течением времени (говоря более техническим языком, что она "нестационарна"), исследователи начали использовать более динамический подход к оценке финансовых активов. В частности, Роберт Энгл, профессор статистики (ранее в Сан-Диего, сейчас в университете Нью-Йорка) и ведущий исследователь в этой области, представил в 1980-х гг. модель волатильности ARCH (авторегрессионная условная гетероскедоктичность) с целью оценки волатильности как авторегрессионного процесса. Ключевой характеристикой модели было то, что она рассматривала волатильность сегодня как функцию волатильности за предыдущий день, а также использовала поправочный коэффициент для отклонений от ожидаемого уровня волатильности. (Роберт Энгл получил Нобелевскую премию по экономике в 2003 г. за работу по моделированию волатильности.)