Определение числа факторов

Одной из задач эксплораторного факторного анализа является задача определения числа факторов. Эта задача по-разному решается в диагональных процедурах и процедурах, основанных на выделении главного фактора.

Как мы уже отмечали, диагональные процедуры факторного анализа, как правило, предполагают выделение определенного числа факторов, заданных рядом исследуемых переменных. В более сложных случаях, как это имеет место, например, в центроидном методе, число факторов определяется на основе специальных процедур анализа исчерпанности корреляционной матрицы. Иногда такую исчерпанность можно определить "на глаз", иногда для этого применяют специальных математические критерии, например критерий Сондерса (Я. Окунь [15]).

Несколько по-иному решается проблема определения числа факторов в процедуре главных факторов. Поскольку полная компонентная модель при применении процедуры главного фактора дает нам в итоге столько факторов, сколько имеется переменных, часть выделяемых факторов признаются несущественными, тривиальными и отбрасываются. Это необходимо для достижения главной цели факторного анализа – уменьшения размерности данных. Наиболее распространенным приемом оценки значимости факторов оказывается сравнение их латентных корней, иначе называемых собственными значениями, с единицей. Этот критерий называют критерием Кайзера. Фактор признается несущественным, тривиальным, если его латентный корень оказывается меньше этой величины. При этом следует обращать внимание на то, какое количество дисперсии описывается этими факторами. Хорошим считается решение, описывающее не менее 80% общей дисперсии в корреляционной матрице.

Другим критерием определения числа нетривиальных факторов в процедуре главных компонент является критерий отсеивания Р. Кеттела. Число факторов определяется па основе графика собственных значений. В качестве критерия отсеивания используется точка перегиба, после которой значения латентных корней перестают меняться в заметной степени.

В любом случае окончательное решение о числе выделенных факторов принимается только после их интерпретации.

Вращение и интерпретация факторов

Допущения, которые предлагаются различными процедурами факторного анализа, такими как, например, центроидный метод или метод главных факторов, обеспечивают однозначное решение уравнения (10.2). Одной из важных задач интерпретации полученного решения является содержательная оценка выделенных факторов. Такая оценка оказывается особенно важной, если используются решения на основе множественных групповых или главных факторов.

Общий подход к решению задачи интерпретации выделенных факторов достаточно прост в теории, хотя и может вызывать некоторые проблемы на практике. Это в значительной степени субъективная процедура, основанная на изучении факторных нагрузок. Обычно исследователь обращает внимание на те переменные, факторные нагрузки для которых оказываются максимально приближенными к единичным значениям. При этом знак факторных нагрузок учитывается так же, как он учитывается в корреляционном анализе.

Например, исследуя факторное решение для шкал семантического дифференциала, Ч. Осгуд [25] обнаружил, что первый из выделенных им факторов в максимальной степени описывается биполярной переменной "хороший – плохой". Таким образом, этот фактор может быть определен как фактор оценки. Второй фактор в структуре семантического дифференциала в исследованиях Ч. Осгуда в наибольшей степени коррелировал с биполярной переменной "сильный – слабый". Поэтому этот фактор был определен как фактор силы. Наконец, третий фактор был определен как фактор активности, так как максимальные нагрузки по этому фактору имела переменная "активный – пассивный".

Однако стоит отметить, что не всегда простая интерпретация полученного факторного решения оказывается возможной с самого начала. В ряде случаев успешной интерпретации факторов может способствовать процедура их вращения.

Для того чтобы понять смысл процедуры вращения, рассмотрим рис. 10.1 (R. Gorsuch [24]). Мы видим, что первый фактор представляет собой комбинацию переменных, связанных с вербальным пониманием и низким уровнем тревоги, тогда как второй фактор отражает комбинацию вербального понимания и высокого уровня тревоги. Такая комбинация переменных на первый взгляд выглядит не совсем понятной. Однако если повернем оси первого и второго факторов примерно на 45° против часовой стрелки, получим более осмысленную интерпретацию факторного пространства. Очевидно, что в этом случае первый фактор окажется фактором вербального понимания, а второй – фактором тревоги.

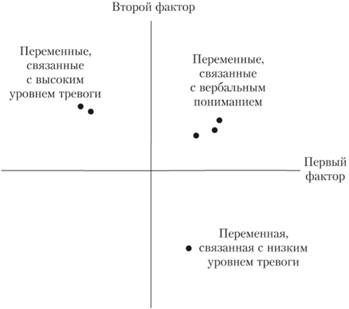
Рис. 10.1. Факторная структура для шести черт личности до вращения

(адаптировано из работы R. Gorsuch [24])

Вращение факторов может осуществляться произвольно, как в рассмотренном нами случае. Чаще же оно представляет собой самостоятельную математическую процедуру. В любом случае имеются две базовые возможности вращения факторов. Один из вариантов вращения основан на модели факторного анализа, предполагающего, что факторы оказываются независимыми друг от друга – ортогональными. Процедура вращения в этом случае сохраняет прямой угол между осями факторов. Поэтому такое вращение называют ортогональным или прямоугольным. Если используется модель факторного анализа, в которой факторы оказываются связанными друг с другом, то и факторное решение оказывается непрямоугольным. В этом случае используют косоугольное, или облическое, вращение факторов.

Наиболее известными и широко применяемыми являются математические процедуры ортогонального вращения факторов. К ним в первую очередь следует отнести процедуры квартимакс и варимакс.

Процедура квартимакс основала на идее упрощения факторного решения. Эта идея еще известна как принцип скупости факторного решения (L. Thurstone [27]). Предполагается, что каждая переменная может высоко коррелировать только с одним фактором. Именно на это нацелена процедура вращения факторов по методу квартимакс.

Процедура варимакс является, по-видимому, наиболее распространенной в психологических исследованиях. Идея вращения по методу варимакс состоит в том, чтобы минимизировать число переменных, имеющих высокие факторные нагрузки с каждым фактором, одновременно увеличивая нагрузки для одного фактора.

Объединением этих двух методов ортогонального вращения являются процедуры эквамакс и ортомакс.

Из косоугольных решений следует отметить процедуру промакс, которая на самом деле является обобщением ортогональных процедур, добавляя возможность изменения угла между факторами. Если исследователь хочет получить решение, предполагающее набор высококоррелирующих друг с другом факторов, стоит выбрать процедуру облимин.