Описание стационарного временно́го ряда авторегрессией и скользящей средней

Для начала рассмотрим общую форму записи моделей авторегрессии со скользящей средней и обсудим то, какие виды прогнозов они позволяют давать.

Модель авторегрессии обычно обозначается в виде AR(p), где р – это порядок модели, который показывает, от какого значения (сколько шагов назад) зависит текущее значение ряда. В общем виде модель AR(p) записывается следующем образом:

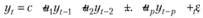(8.1)

где с – константа; аi – i-й коэффициент модели; εt – ошибка модели, о которой, конечно же, предполагается, что она распределена независимо и нормально с нулевым математическим ожиданием и некоторой постоянной дисперсией.

Коэффициенты модели (8.1) легко рассчитываются обыкновенным методом наименьших квадратов. Значимость коэффициентов полученной модели определяется стандартными эконометрическими методами.

Часто для упрощения представления модели авторегрессии вводят так называемые лаговый оператор – функцию, согласно которой

(8.2)

Само ОГЛАВЛЕНИЕ оператора совершенно неважно, просто записывать модель авторегрессии высокого порядка с ним значительно легче. Например, модель (8.1) в общем виде с помощью (8.2) может быть переписана в другой форме:

(8.3)

Если теперь в (8.3) справа оставить лишь ошибку и константу, а влево перенести все остальные элементы, то можно получить общепринятую форму записи модели авторегрессии порядка р:

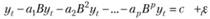(8.4)

Вынося в (8.4) уt за скобки, получим

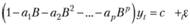(8.5)

Составляющую в скобках можно представить как функцию от оператора сдвига:

(8.6)

Это позволяет представить авторегрессию в еще более компактном виде:

(8.7)

Здесь нижний индекс в самой функции определяет порядок авторегрессии, а указание на В в скобках – то, как будут представлены элементы в (8.6). Например, для авторегрессии третьего порядка AR(3) получим

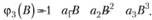(8.8)

Подставляя (8.8) в (8.7), перегруппировывая элементы, мы в итоге придем к модели:

Как видим, форма (8.7) удобна благодаря своей компактности. Стоит также отметить, что авторегрессия (8.7) обычно рассматривается без константы, но ее наличие не критично, так как оно лишь меняет уровень ряда. Сам смысл модели от нее не меняется.

Чтобы дать прогноз по модели AR(p) на один шаг вперед, достаточно подставить в оцененное уравнение имеющиеся фактические значения на последних наблюдениях. Однако для того, чтобы дать прогноз на два шага вперед и более, нужно сделать допущение, идентичное тому, которое было в экспоненциальном сглаживании:

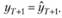(8.9)

В случае с простейшими моделями это допущение позволяет определить прогноз на h шагов вперед. В случае с более сложными моделями приходится использовать итеративную процедуру: рассчитав прогноз на один шаг вперед, подставлять его в формулу для того, чтобы получить прогноз на два шага вперед, и т.д.

Рассмотрим свойства простейшей авторегрессионной модели – модели авторегрессии первого порядка AR(1), известной также под названием "Марковский процесс". В общем виде она может быть записана как

(8.10)

Если по этой модели дать прогноз на один шаг вперед, то получим

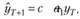(8.11)

Для получения прогноза на два шага вперед подставим полученное в (8.11) значение в модель:

(8.12)

Раскрывая скобки в (8.5), получаем формулу для расчета прогноза на два шага вперед по модели AR(1):

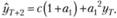(8.13)

Повторяя такую итеративную процедуру, получим формулу для расчета прогноза на h шагов вперед:

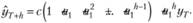(8.14)

В формуле (8.14) сумма в скобках – это сумма элементов геометрической прогрессии, которая равна

(8.15)

Подставляя (8.15) в (8.14), получаем простую формулу для расчета прогнозного значения на h шагов вперед на основе последнего полученного фактического значения:

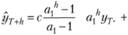(8.16)

Можно заметить, что прогнозное значение в формуле (8.16) зависит в первую очередь от значения коэффициента а1, причем зависимость эта носит вид показательной функции (5.38), рассмотренной нами в параграфе 5.3. Соответственно прогноз по модели AR(1) будет представлять собой достаточно простые траектории показательного характера, которые мы уже рассматривали. Напомним их. На рис. 8.1 приведены четыре возможных варианта прогнозных траекторий.

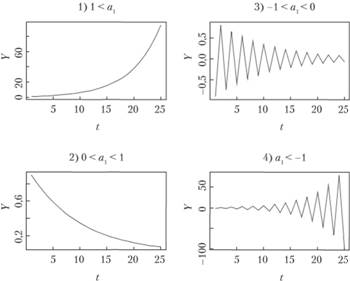
Рис. 8.1. Виды прогнозных траекторий для модели AR(1)

Наибольший интерес в прогнозировании представляют траектории с а1 > 0. Однако стоит отметить, что при построении модели ARMA ситуаций, наподобие той, когда а1 > 1, стараются избегать в связи с тем, что при таких значениях коэффициента модель становится нестационарной. Подробнее вопросы стационарности мы рассмотрим в следующем параграфе.

Процесс, в котором а1 = 1, называется процессом случайного блуждания, так как в таком случае в формировании будущего значения уt основную роль играет уже не предыдущее значение уt-1, а ошибка

Такой процесс занимает отдельное место в эконометрике, потому что теоретически лежит в основе множества нестационарных процессов. Графический пример процесса случайного блуждания приведен на рис. 8.2.

Рис. 8.2. Процесс случайного блуждания

В связи с тем что ошибки г, были заданы i.i.d. (независимо одинаково распределенными) по стандартному нормальному закону, на каждом конкретном наблюдении t могло получиться как положительное, так и отрицательное отклонение от уt-1. В результате этого могут получаться совершенно разные траектории в совершенно разных направлениях. Естественно, в связи с тем, что ошибки на периоде прогнозирования предполагаются равными нулю, прогноз по модели случайного блуждания соответствует прогнозу по модели Naive – все будущие значения равны последнему полученному фактическому. Этот тип модели не используют непосредственно в прогнозировании с помощью авторегрессий, но скорее используют как инструмент для идентификации временны́х рядов.

Обратим внимание на то, что порядок авторегрессии имеет особое значение – это не просто сдвиг наблюдений на шаг или два назад, а существенное изменение сути модели.

Вторая по популярности модель авторегрессии – это модель AR(2), известная также под названием "Процесс Юла". В компактной форме она записывается как

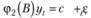(8.17)

А в более подробном представлении имеет вид

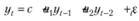(8.18)

Прогнозирование на один шаг вперед с помощью этой модели осуществляется так же просто, как и с помощью AR(1):

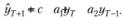(8.19)

Однако прогноз на произвольное число шагов вперед h требует уже рекуррентной процедуры с расчетом всех промежуточных значений между наблюдениями Т + 1 и Т + h.

Эта модель позволяет получать значительно большее число прогнозных траекторий, и рассмотреть все из них достаточно затруднительно. Несколько примеров таких траекторий приведены на рис. 8.3.

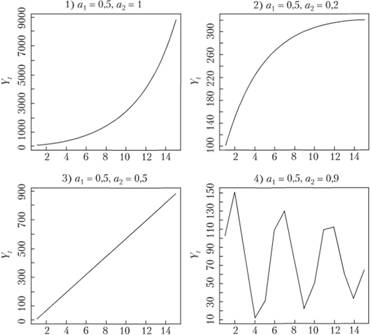
Рис. 8.3. Виды прогнозных траекторий для модели AR(2)

Ситуации, изображенные в левой части графика, соответствуют нестационарным моделям, к которым в практике прогнозирования стараются не обращаться.

Как видим, при разных значениях коэффициентов а1 и а2 можно получить совершенно разные траектории: линейные, экспоненциальные, с асимптотой, тригонометрические и т.д. В связи с тем что расчет коэффициентов осуществляется с помощью МНК, выбранная траектория автоматически должна наилучшим образом соответствовать ряду данных.

Условие стационарности для модели AR(2) записывается в виде системы неравенств:

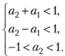(8.20)

Более сложные модели позволяют моделировать еще более разнообразные и сложные прогнозные траектории. Однако в прогнозировании стараются избегать моделей авторегрессии порядка больше двух. Иногда это условие ослабляется до третьего порядка. Вызвано такое ограничение тем, что обычно появление элементов более высокого порядка сигнализирует о наличии сезонности в ряде данных, а для ее моделирования с помощью авторегрессий есть специальные модификации (например, модель SARIMA, к которой мы обратимся позже).

Идея о том, что исследуемая величина может зависеть от своих же значений в прошлом, получила дальнейшее развитие. Так, предполагая, что при генерации yt всегда существует некоторая ошибка (которая, конечно же, распределена нормально, что указывает на влияние множества мелких неучтенных факторов), появилась идея о том, что будущие значения уt могут зависеть не только от прошлых значений ряда, но и от случайных ошибок на предыдущих наблюдениях. Так появилась модель скользящей средней порядка q, MA(q), которая обычно записывается в виде

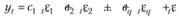(8.21)

В связи с тем что в (8.21) будущие значения зависят от предыдущих ошибок, рассчитать коэффициенты модели МНК уже невозможно. Поэтому при оценивании модели используются численные методы.

Стоит отметить, что сумма весов при ошибках в (8.21) необязательно равна единице, поэтому название "скользящая средняя" не совсем соответствует действительности. Однако это название уже давно закрепилось за этой моделью.

Используя введенный нами ранее лаговый оператор В, формулу (8.21) можно переписать в виде

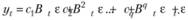(8.22)

Вынося в (8.22) за скобки ε„ получим

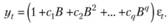(8.23)

По аналогии с авторегрессией введем функцию для приведения (8.23) к компактному виду:

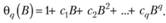(8.24)

Здесь нижний индекс в функции так же, как и в случае с авторегрессией, определяет порядок модели.

Стоит обратить внимание, что для единообразия записи Дж. Бокс и Г. Дженкинс использовали другое представление функции (8.24):

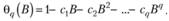
В таком виде она похожа на функцию (8.6) для авторегрессии и с ней удобнее работать при оценке стационарности ряда. Однако смысла в таком искажении параметров модели в данном случае нет, потому что к такой зависимости можно прийти, лишь предположив, что первоначальная модель (8.21) должна иметь другой вид: – что на самом деле неудобно. Именно поэтому здесь и далее мы будем использовать функцию (8.24), следующую из модели (8.21).

С учетом (8.23) модель скользящего среднего порядка q может быть компактно записана как

(8.25)

Чтобы дать прогноз по модели МA(q) на h шагов вперед, нужно вначале дать прогноз на один шаг вперед, а дальше допустить, что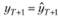

В связи с тем что ошибка рассчитывается как отклонение фактического значения от расчетного, на периоде прогноза все ошибки обращаются в нуль: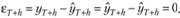

Поэтому прогноз по модели МА(q) на h шагов вперед представляет собой простую прямую линию: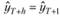

Модель скользящей средней обычно ограничивают вторым, а иногда – третьим порядком. Вызвано это все теми же соображениями, что и в случае с авторегрессией.

Обратим внимание на то, что для того чтобы получить ошибки, по которым далее можно запустить модель, в модели скользящего среднего требуется задать какие-то стартовые значения εt. Обычно для этого пользуются процедурой "обратного прогноза" (Backcast), с помощью которой восстанавливают значения ошибок. Выводятся эти значения с помощью самой модели. Обычно при этом предполагается, что значения на лагах t + 1 и t – 1 коррелируют со значением t одинаково. Поэтому значение ряда можно получить, используя не только предыдущие, но и будущие значения. В результате этого для модели (8.21) значения ошибок на наблюдении t будут вычисляться по формуле

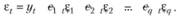(8.26)

Вычисляя ошибки для всего ряда данных с конца до самого начала по формуле (8.26), можно получить ряд стартовых значений ошибок, состоящий из q элементов. Очевидно, что полученные таким образом ошибки будут уже по-другому влиять на расчетные значения у, поэтому процедура обратного прогноза носит итеративный характер: после получения оценок по формуле (8.26) коэффициенты модели переоцениваются. Затем стартовые значения опять вычисляются, и так продолжается до получения устойчивых оценок коэффициентов.

Процессы AR(p) и МА(q) связаны друг с другом. Так, если обратиться к модели авторегрессии (8.7) в компактном виде без константы и выразить в ней уt, то получим

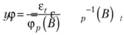(8.27)

При этом, если в исходной модели авторегрессии (8.1) попытаться выразить текущее значение уt через предыдущие, используя саму же формулу (8.1), то мы получим бесконечный ряд ошибок с коэффициентами авторегрессионной модели, что может быть компактно записано в виде

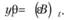(8.28)

Из этого следует, что авторегрессии конечного порядка соответствует процесс скользящей средней бесконечного порядка и наоборот.

Покажем это свойство на примере модели AR(1) без константы:

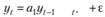(8.29)

Из (8.29) следует, что значение yt-1 рассчитывается по формуле

(8.30)

Подставляя (8.30) в (8.29), получим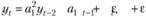

Выражая значение на шаге t через фактическое значение на шаге t – 3, получим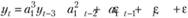

В общем случае значение yt может быть рассчитано через значение :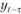

(8.31)

В (8.31) в случае со стационарным процессом 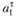с приближением τ к бесконечности будет приближаться к нулю. Тогда, устремляя τ в бесконечность, получаем формулу, выраженную в терминах скользящей средней:

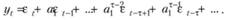(8.32)

Используя лаговый оператор и компактный вид, приходим к модели скользящей средней бесконечного порядка (8.28).

Аналогично можно показать, что конечным процессам МА(q) соответствуют бесконечные AR. Все это указывает на то, что модели авторегрессии и скользящего среднего можно объединить для того, чтобы конечными порядками описывать соответствующие составляющие. Модель ARMA(p,q) в первоначальном виде записывается так:

(8.33)

Используя введенные нами ранее лаговые операторы и функции (8.6) и (8.24), формулу (8.33) можно переписать в компактном виде:

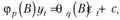(8.34)

Так, например, модель ARMA(2,1) будет иметь вид 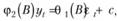откуда

или в полной форме:

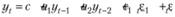
Модель ARMA сочетает в себе свойства как авторегрессии, так и скользящей средней. А в связи с тем, что на участке прогноза ошибки обращаются в нуль (элементы МА обращаются в нуль), все прогнозируемые траектории ARMA(p,q) будут соответствовать траекториям AR(p). Однако это не означает, что скользящая средняя не нужна – ее учет позволяет более точно аппроксимировать ряд данных и отсечь ненужные элементы авторегрессии, которые возникли бы из-за связи между AR и МА.