Объектно-ориентированный подход

Объектно-ориентированный подход обладает достаточно мощным и универсальным формализмом, с помощью которого можно описывать поведение экономических агентов на рынках. Объектно-ориентированный формализм, а также преимущества средств объектно-ориентированного проектирования и программирования позволяют не только успешно моделировать организационные структуры в виде систем объектов (агентов), но также строить и динамически развивающиеся структуры, учитывая наличие у агентных структур следующих свойств.

1. Активный характер объекта, позволяющий говорить о нем как об элементе структуры, инкапсулирующем свойства (состояние) и обладающем определенным поведением.

2. Существование значительных резервов повышения эффективности эвристического метода оптимизации при переходе к объектно-распределенным алгоритмам, таким как возможности:

o распараллеливания вычислений;

o реализации в распределенных вычислительных средах;

o организации конкурирующего поиска по объектам;

o осуществления поиска в динамических структурах;

o обучения объектов в процессе осуществления поиска.

3. Наличие множества программных сред проектирования многоагентных систем, а также объектно-ориентированных языков программирования, упрощающих их разработку и реализацию.

Таким образом, можно говорить о нейроподобных агентных системах, так как функционирование такой структуры основывается на принципах действия нейронных сетей, предусматривающих обучение для минимизации функции ошибки. Теоретическая основа метода изложена в работах D. Е. Rumelhart, G. Е. Hilton, R. J. Williams, С. И. Барцева, В. И. Городецкого, В. А. Охонина, а также в более ранних работах Ж. Лагранжа, Лежандра и других ученых. Моделирование поведения организационных структур с помощью процессов обучения агентной структуры основывается на эвристической стратегии.

Агентную систему формально можно описать как объединение множества типов данных Г, алфавита событий X, множества идентификаторов объектов /, классов (объектных моделей) С и объектов О (формализм взят из материалов европейских конференций по объектно-ориентированному программированию ЕССОР):

S = (Т, Х, I, С, О).

Пусть имеется множество входов Х₀ = {x₁, x₂, ..., х_n}, содержащих параметры внешней среды, и выход у системы (ее реакция на внешние воздействия), для которых получена обучающая выборка. Мы будем рассматривать обучающую выборку как зависимость соответствующих переменных от относительного (дискретного) времени t, т.е. х_i = x_i(t) и у = y(t), где t = 0, 1, ..., ∞. Состояния входов и выхода системы инкапсулируют структурные элементы INput = (х) и OUTput = (у), которые в рамках объектно-ориентированного формализма являются классами.

Далее будем рассматривать множество Х₀ как множество экземпляров класса INput, а у - как экземпляр класса OUTput. Введем также класс преобразующего структурного элемента FUNction = (IN, N, Ху f()), который в качестве атрибутов содержит ссылки на связываемые структурные элементы (связи) - множество IN, результат преобразования - переменную х, а также функцию преобразования входов в переменную х - метод f(). IN={inj} - множество ссылок на входы или преобразующие структурные элементы, N - число входов (будем обозначать N_i = о_i,N). Обращение по ссылке будем обозначать, используя синтаксис языка C++, т.е. (*inj)x, это обращение к переменной элементах, доступного по j-й ссылке (связи).

При создании структурного элемента FUNction результат преобразования будем рассматривать как дополнительный вход структуры х, который может использоваться в других преобразованиях, что достигается наследованием класса INput. При этом множество переменных {х_i} входов (и преобразующих структурных элементов в том числе), мы будем рассматривать как множество переменных X. Множество типов преобразующих структурных элементов представлено подклассами класса FUNction. Обозначим множество экземпляров преобразующих структурных элементов указанных типов О. Принадлежность объекта о классу с будем обозначать class(o) = с, наследование объектом класса с - superclass(o) = с.

Самоорганизующейся агентной структурой будем называть объединение множеств

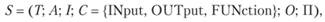
где Т - множество типов данных объектной системы; А - алфавит событий объектной системы; I - множество идентификаторов объектов; С = {INput, OUTput, FUNction} - множество классов структурных элементов (агентов); О = {o_i} - множество элементов структуры; П - множество правил самоорганизации данной структуры.

Множество переменных структуры можно определить как

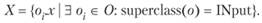
Множество входов для обучающей выборки:

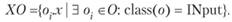
Множество выходов, состоящее в нашем случае из одного элемента:

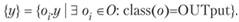
Требуется найти стратегию П организации структуры, при использовании которой в течение ограниченного времени и на базе существующих вычислительных ресурсов будет найдена структура, аппроксимирующая зависимость входов X и выхода у с заданной точностью. В качестве критерия наилучшей аппроксимации будем использовать следующий:

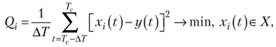
где Т_с - текущий момент времени структуры; ΔТ - период измерения качества аппроксимации. Введение интегрального критерия обусловлено необходимостью снижения трудоемкости по сравнению с использованием статистических оценок ошибок аппроксимации.

Самоорганизация структуры включает в себя всевозможные преобразования над агентами и связями. Для упрощения анализа мы будем под стратегией самоорганизации структуры понимать стратегию, состоящую из правил настройки структурных элементов Пн, т.е. мы сознательно исключаем из рассмотрения модификации структуры, связанные с созданием и уничтожением агентов.

Показателями эффективности такой самоорганизации структуры выступают: максимальное качество аппроксимации и минимальное время построения. При сравнении стратегий основным критерием является время построения структуры, которая способна аппроксимировать с заданным уровнем ошибки. Если заданный уровень ошибки не достигнут, то в рассмотрение берется качество аппроксимации.

Дискретный характер процессов позволяет выражать время построения через число итераций процесса построения, обозначим Т_постр. Качество аппроксимации определим как:

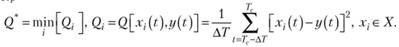
Условие достижения заданного уровня ошибки можно записать в виде 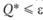. Тогда критерий оптимальности стратегии построения следующий:

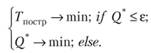
Введем в задачу еще несколько необходимых ограничений, касающихся свойств функций преобразования структурных элементов о_if (). Во-первых, будем считать, что все переменные (входные и выходные) принадлежат к одному типу данных. Тогда в качестве функций преобразования рассмотрим различные операции, в общем случае n-арные, определенные на пространстве значений данного типа данных. Во-вторых, будем требовать для унарных операций выполнения условий замкнутости, однозначности, полной определенности, обратимости. Для остальных - замкнутости, однозначности, полной определенности и разрешимости уравнений с одним неизвестным (деление) по всем переменным. Тип операции (функции преобразования) соответствует классу структурного элемента с_j ∈ С, т.е. имеется однозначное соответствие с_j → f_j. Или для индексирования по объектам fo_i = fj: class(o_i) = с_j ∈ С.

Таким образом, на основании системного подхода проведена формализация модели коммуникационного процесса, лежащего в основе информационной системы на языке теории множеств. Выявлены системные закономерности, присущие процессу формирования информационной системы.

На базе информационного подхода рассмотрены концепции понятий "информация", "информатизация", "информатика", "информационная деятельность" и "информационное обслуживание", которые позволили определить сущность информационных процессов.

На основании стратегического подхода сформулированы принципы формирования стратегий развития информационной системы и информационных технологий, определены миссия, цели, функции и этапы жизненного цикла информационной системы.

С помощью объектно-ориентированного подхода построена математическая модель многоагентной структуры, которая описывает процессы девальвации организационной структуры при изменении параметров влияния внешней среды.