Объединенная модель

Объединенная модель представляет обычную линейную модель регрессии и описывается уравнением

(9.6)

При этом ошибки 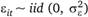, т.е. ошибки eic являются независимыми, одинаково распределенными величинами (iid – independent identically distributed) с математическим ожиданием E(cit) = 0 и дисперсией ν(εί()σ= . Также ошибки еи не коррелируют между собой по і и по t и не коррелируют со всеми независимыми переменными xir

Объединенная модель получается, если собрать все данные по i и по t в одну большую регрессию с NT наблюдениями. Объединенная модель фактически не учитывает панельную структуру данных и не позволяет реализовать потенциал панельных данных, в частности индивидуальные характеристики отдельных изучаемых единиц.

Модель с фиксированными эффектами

Модель с индивидуальными фиксированными эффектами имеет вид

(9.7)

В модели (9.6) индивидуальные эффекты измеряют ненаблюдаемую неоднородность, xit и β представляют собой матрицы размерностью к χ 1 и ошибки eit являются независимыми одинаково распределенными величинами с математическим ожиданием и дисперсией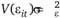

Термин "фиксированные эффекты" означает, что константа в уравнении регрессии может различаться между индивидами, но для каждого конкретного индивида константа является постоянной во времени, т.е. не изменяется с течением времени t.

Для линейной модели с фиксированными эффектами существует несколько способов, для того чтобы получить состоятельные оценки β-коэффициентов, несмотря на присутствие мешающих параметров а;:

• оценивание обычным методом наименьших квадратов во внутригрупповой модели;

• прямое оценивание обычным методом наименьших квадратов модели с фиктивными переменными для каждого из N фиксированных эффектов;

• оценивание условным методом максимального правдоподобия в модели с фиксированными эффектами;

• оценивание обычным методом наименьших квадратов в модели первой разности.

Внутригрупповые оценки, или оценки с фиксированными эффектами

Рассмотрим модель с фиксированными эффектами (9.7). Если из уравнения регрессии (9.7) вычесть уравнение, записанное в средних по времени значениях для каждого индивида

где

то получим внутригрупповую модель (within-group model), построенную по отклонениям от групповых средних,

(9.8)

В отличие от первоначальной модели (9.7) внутригрупповая модель (9.8) уже не содержит фиксированные эффекты а,•.

Межгрупповая модель (between-group model) представляет собой регрессию у і = X; β +,<х которая может быть переписана в виде

(9.9)

где– составные ошибки.

В межгрупповой модели используется вариация между различными индивидами, и межгрупповая модель является аналогом пространственной регрессии, которая представляет собой частный случай для Т = 1.

Уравнения (9.7)–(9.9) – классические регрессионные модели, и их можно оценивать обычным методом наименьших квадратов, при помощи которого можно получить если не эффективные, то по крайне мере состоятельные оценки коэффициентов. Рассмотрим МНК-оценки β-коэффициентов для каждого из этих трех уравнений и определим, как они взаимосвязаны. Для нахождения оценок коэффициентов нам понадобятся суммы квадратов и смешанных моментов.

В уравнении (9.7) моменты отражают вариацию от общих средних у их, суммы квадратов и смешанных моментов будут иметь вид

(9.10)

(9.11)

В уравнении (9.8) данные представлены в виде отклонений от групповых средних, и суммы квадратов s^yTp и смешанных моментов s^,yTP будут отражать внутригрупповые суммы квадратов

(9.12)

(9.13)

Для уравнения (9.9) суммы квадратов sl^* и смешанных моментов будут отражать межгрупповые суммы квадратов

(9.14)

(9.15)

При этом выполняются равенства и

МНК-оценки β-коэффициентов для уравнения регрессии (9.7) будут определяться следующим образом:

(9.16)

Оценивая уравнение регрессии (9.8) для отклонений от групповых средних, получим МНК-оценки β-коэффициентов, которые называют внутригрупповыми оценками, или within-оценками (within-groups estimators):

(9.17)

Оценивая уравнение (9.9), получим межгрупповые МНК- оценки β-коэффициентов (between-groups estimators), которые также называют оценками групповых средних, или between- оценками:

(9.18)

Из уравнений (9.17) и (9.18) следует, что и . Тогда можно показать, что

(9.19)

Получается, что общая МНК-оценка β-коэффициентов представляет собой средневзвешенное значение внутригрупповых и межгрупповых МНК-оценок β-коэффициентов.

Межгрупповые оценки β-коэффициентов будут состоятельными в том случае, если регрессоры Зс, не коррелируют с составными ошибками . Однако в модели с фиксированными эффектами предполагается, что а, коррелируют С Xit, и следовательно, коррелируют С Xj.

Внутригрупповая оценка – это состоятельная оценка β-коэффициентов в модели с фиксированными эффектами в отличие от оценки объединенной модели и межгрупповой оценки, которые являются несостоятельными. Внутригрупповая оценка измеряет связь между индивидуальными отклонениями регрессоров от их средних по времени значений и индивидуальными отклонениями зависимой переменной от ее среднего по времени значения.

Внутригрупповую оценку также называют оценкой с фиксированными эффектами , так как она является эффективной оценкой β-коэффициентов в модели (9.7) в том случае, если а, представляют собой фиксированные эффекты и ошибки cit являются независимыми, одинаково распределенными величинами с нулевым математическим ожиданием и дисперсией of. Внутригрупповые оценки совпадают с МНК- оценками с фиктивными переменными (LSW-оценками).

Главное ограничение внутригрупповых оценок состоит в том, что во внутригрупповой модели невозможно оценить коэффициенты при регрессорах, которые остаются постоянными для г-го индивида, т.е. не изменяются с течением времени t. Действительно, xit – xi = 0 в том случае, если xit = хi, для всех і. Однако многие исследователи заинтересованы в оценивании воздействия регрессоров, постоянных во времени, для каждого индивида. В качестве таких регрессоров, например, могут выступать пол, раса, вероисповедание индивида. Для этих целей исследователи предпочитают не использовать внутригрупповые оценки. Оценки объединенной модели или оценки со случайными эффектами позволяют оценить коэффициенты при объясняющих переменных, которые не меняются во времени и постоянны для каждого индивида, но если корректной моделью является модель с фиксированными эффектами, то эти оценки будут несостоятельными.

Из уравнения (9.12), (9.13) и (9.17) следует, что внутригрупповые МНК-оценки β-коэффициентов определяются по формуле

(9.20)

После того, как оценки [}внутр стали известными, могут быть оценены индивидуальные эффекты а,•:

(9.21)

Найденные таким образом оценки ά; будут несмещенными оценками индивидуальных эффектов а,-. Состоятельность оценки ά,• обеспечивается условием Г -> оо, так как а, выступает в качестве среднего значения для Т наблюдений. В коротких панелях оценки ά; являются несостоятельными, однако оценки рвнутр будут состоятельными. Коэффициенты а, можно рассматривать как мешающие параметры или вспомогательные параметры, и нет необходимости в том, чтобы они были состоятельно оцененными для получения состоятельных оценок наиболее важных для нас параметров β. Однако этот результат не стоит переносить на более сложные модели с фиксированными эффектами, например такие, как нелинейные модели.

Внутригрупповые оценки βΒΗγτρ являются состоятельными, если

(9.22)

Этот предел по вероятности может быть равным нулю в том случае, если или , или и (9.23)

Принимая во внимание то, что х( и ε; являются средними величинами, можно показать, что достаточным условием для уравнения (9.23) будет выполнение строгого экзогенного условия, состоящего в том, что

Так как во внутригрупповой модели ошибкикор

релируют по t для данных і, то распределение |Звнутр получается потенциально сложным, но, несмотря на это, можно применять результаты обычного метода наименьших квадратов. При строгом предположении о том, что £и являются независимыми одинаково распределенными величинами с нулевым математическим ожиданием и дисперсией σ%, дисперсия оценки βΒΗγτρ будет иметь вид

(9.24)

Для дисперсии ошибок состоятельной и несмещенной оценкой будет оценка

(9.25)

где число степеней свободы равно размеру выборки NT без числа оцененных параметров к и индивидуальных эффектов N.

Для коротких панелей достигается робастная оценка асимптотической дисперсии

(9.26)

Эта предпочтительная оценка допускает произвольную автокорреляцию для ошибок Eit и произвольную гетероскедастичность.

Если N является слишком большим, то альтернативным и более простым способом вычислить внутригупповые оценки будет способ посредством МНК-оценок с фиктивными переменными.