Научная база управления логистическими процессами
Центральным пунктом в логистике является обеспечение руководителей организации научной базой для решения различных проблем и принятия решений, которые возникают в практической деятельности. Для этого используются различные экономические и математические подходы.
В логистическом менеджменте используются в основном три подхода: научный подход, системная ориентация и моделирование процессов (использование моделей).
Научный подход должен базироваться на наблюдениях за проблемой (сбор и анализ полученной информации), следующий шаг связан с формированием гипотезы, т.е. установлением зависимости между компонентами проблемы по данным наблюдений и проверкой гипотезы. Если гипотеза верна, то происходит ее реализация, если нет, то проводятся новые исследования и гипотеза уточняется.
Системная ориентация связана с тем, что организация приводится в единую систему.
Моделирование процессов связано с использованием экономико-математических моделей.
Существует множество разновидностей моделей.
1. Алгебраические модели. Алгебра – это основной математический инструмент. Он может быть использован для решения операционных проблем, таких, например, как анализ практической точки и анализ затраты-прибыль.
2. Статические модели. Многие логистические решения могут включать неопределенность, для таких задач рекомендуется использовать вероятностное распределение и статистическую теорию. Представим три вида статистических моделей:
а) прогнозирование – процесс создания проекций па будущее таких переменных, как продажи (товарооборот регионального склада), объем материалопотока, затраты;
б) контроль качества – помогает измерять и регулировать степень соответствия, до которой продукт (перемещение) или сервис отвечает специфическим стандартам логистики;
в) теория решений – используется в деревьях решений и таблицах решений, чтобы помочь представить и решить проблемы при условии риска.
3. Экономико-математические модели. В настоящее время данные модели применяются для принятия оптимальных решений в различных областях экономики. В основе экономико-математических исследований лежит математическое моделирование изучаемого экономического процесса, т.е. описание количественных закономерностей этого процесса с помощью математических выражений. Экономикоматематическая модель является абстрактным отображением реального процесса и в меру своей абстрактности может его характеризовать более или менее точно. Модель представляет собой экономико-математическое выражение в виде систем уравнений, неравенств, функций, количественных зависимостей в каком-либо реальном логистическом процессе.
Экономико-математическая модель состоит из трех составляющих. Первая составляющая – целевая функция, она отражает принятый критерий (мерило) эффективного решения задачи. От правильности выбора целевой функции зависит ценность полученных результатов. Второй составляющей экономико-математической модели служат системы уравнений и неравенств, выражающие условия (или ограничения), которые должны соблюдаться при решении задачи. Третьей составляющей является требование формального порядка, т.е. условие неотрицательности, которое состоит в том, чтобы все переменные величины задачи принимали только неотрицательное значение.
Все экономико-математические модели можно разделить на детерминированные, стохастические и модели с элементами неопределенности.
Детерминированными называются такие модели, в которых с абсолютной достоверностью описываются как условия (ограничения), так и подлежащий оптимизации критерий (целевая функция). Все величины, используемые в таких моделях, детерминированы, т.е. не случайны. Они могут быть линейными, динамическими и графическими.
Среди математических методов наиболее разработаны методы линейного программирования. Слово "линейное" определяет математическую сущность метода, которая заключается в том, что с его помощью решают задачи с линейными связями и ограничениями, т.е. если выразить задачу в математической форме, то в ней все неизвестные будут в первой степени. Общая идея линейного программирования основана на методе выбора оптимального варианта из множества возможных путей. Существуют различные методы линейного программирования, представляющие собой разные способы вычислений, наиболее удачно приспособленные к той или иной конкретной задаче и, по возможности, быстро ведущие к цели.
В динамических моделях рассматриваются системы, изменяющиеся во времени иод внутренним и внешним воздействием. Расчет динамических моделей сложен, и для каждой конкретной задачи необходимо разрабатывать специальный алгоритм решения.
Графические модели используются тогда, когда задачу удобно представить в виде графической структуры.
Разные интерпретации задач – геометрическая, матричная и др. – позволяют использовать и разные способы вычислений – графический, симплексный, распределительный, каждый из которых имеет свои разновидности.
Стохастическими (вероятностными) называются такие модели, в которых имеется неопределенность, т.е. когда условия (ограничения), или подлежащий оптимизации критерий (целевая функция), или и то и другое являются какой-либо числовой характеристикой (например, математическим ожиданием) случайных величин. К стохастическим моделям можно отнести модели теории массового обслуживания, а также модели теории полезности, поиска и принятия решений.
Для моделирования ситуаций, зависящих от факторов, для которых невозможно собрать статистические данные, и значения которых не определены, используются модели с элементами неопределенности. Для названных экономикоматематических моделей существуют стандартные методы решения, которые будут в дальнейшем использованы при решении логистических проблем.
Кроме использования экономико-математических методов и моделей необходимо проводить и глубокий анализ экономических данных логистической системы. Задача экономического анализа заключается не только в том, чтобы установить факты и констатировать цель событий и регулярность их наступления, но и в том, чтобы указать место проявления этих фактов, выявить закономерность, которая позволит сделать ряд выводов для оценки прошлого и прогноза развития спроса в будущем. Наиболее распространенным методом обработки информации о спросе является пересчет абсолютных показателей в относительные, поскольку экономист в результате анализа выражает показатели средними или относительными величинами.
Для изучения структуры поступления и спроса продукции широко применяются величины в виде долей и процентов. В общем виде эти относительные величины можно определить следующим образом:
 или
или 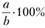 , (2.1)
, (2.1)
где а – поступление и спрос отдельной группы товаров; b – общее количество поступления и спроса товаров.
Пример 2.1
Дано:
b = 200 тыс. усл. ден. ед.; а = 50 тыс. усл. ден. ед.
Определить долю и процент на спрос отдельной группы товаров.
Решение.
Определяем долю:  .
.
Определяем процент:  .
.
С помощью разных величин можно получить различные показатели развития спроса.
Пример 2.2
Дано:
1) продажа товара за год составляет 150 000 усл. ден. ед.;
2) количество обслуживаемых фирм, предприятий равно 5000 ед.
Определить среднемесячный и среднедневной оборот продажи
продукции, которая приходится на одну фирму.
Решение.
1. Среднемесячный оборот, усл. ден. ед.: 150 000 : 12 = 12 500.
2. Продажа продукции, приходящаяся на одну фирму, усл. ден. ед.: 150 000 : 5000 = 30.
3. Среднедневной оборот, усл. ден. ед.: 150 000 : 360 = 416,6.
По этим показателям можно исчислить еще ряд относительных
показателей (среднедневную, среднемесячную продажу).
Для прогнозирования материалопотока можно использовать динамические ряды, которые показывают его изменение во времени. В зависимости от исходных данных в качестве главных уравнений могут быть выбраны различные типы кривых или прямая линия. Эти типы кривых или прямая линия могут выражаться следующими функциями:
 – степенна́я зависимость;
– степенна́я зависимость;
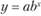 – показательная зависимость;
– показательная зависимость;
 – уравнение гиперболы; (2.2)
– уравнение гиперболы; (2.2)
 – уравнение прямой;
– уравнение прямой;
 – многочлен целых степеней, где у – значение спроса; х – значение фактора; а, b – коэффициенты.
– многочлен целых степеней, где у – значение спроса; х – значение фактора; а, b – коэффициенты.
Для изучения спроса на материалопоток применяется факторный анализ, который позволяет установить виды связи, существующие между спросом и основными факторами, определяющими его уровень.
Для установления вида связи используется теория корреляции. Ее использование в факторном анализе связано с двумя задачами:
1) выявление зависимости в фактическом информационном материале и определение формы связи;
2) измерение силы и тесноты связи.
Первая задача решается при обработке материала – ранжированием, группировкой и выводом уравнения корреляционной связи, вторая – расчетом специальных показателей тесноты связей (коэффициента корреляции, индекса корреляции, корреляционного отношения).
Показателем тесноты связи между фактором и спросом на продукт является коэффициент корреляции.
В случае линейной функциональной связи между фактором и спросом коэффициент корреляции rxy равен +1 при прямой связи и -1 при обратной связи. При отсутствии связи он равен 0.
Если связь положительная, коэффициент корреляции находят в интервале от 0 до +1, если отрицательная, то в интервале от 0 до -1.
Коэффициент корреляции можно рассчитать по следующим формулам:
 или
или , (2.3)
, (2.3)
где х – значение фактора; у – значение спроса; 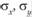 – средние квадратические отклонения по показателям фактора и спроса соответственно; п – динамический ряд;
– средние квадратические отклонения по показателям фактора и спроса соответственно; п – динамический ряд;
 (2.4)
(2.4)
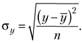 (2.5)
(2.5)
В случае многофакторного анализа тесноту связи определяют через другой показатель:
 (2.6)
(2.6)
где 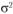 – дисперсия частных средних
– дисперсия частных средних  ;
; 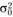 – дисперсия всех
– дисперсия всех
значений у относительно их общей средней.
Факторы, формирующие спрос, не всегда могут быть выражены в количественных показателях. Для установления тесноты связи спроса с такими факторами применяется ранговый коэффициент корреляции:
 (2.7)
(2.7)
где d – разность между рангами (порядковыми номерами) в двух рядах; п – число сопоставляемых пар.
При анализе информации о покупательском спросе применяют коэффициент эластичности (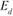 ):
):
 , или
, или  , (2.8)
, (2.8)
где  – первоначальное количество спрашиваемой продукции, ед.;
– первоначальное количество спрашиваемой продукции, ед.; 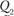 – измененное количество спрашиваемой продукции, ед.;
– измененное количество спрашиваемой продукции, ед.; 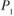 – первоначальная цена, усл. ден. ед.;
– первоначальная цена, усл. ден. ед.;  – измененная цена, усл. ден. ед.
– измененная цена, усл. ден. ед.
В экономической теории считают, что спрос при 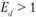 – эластичный; при
– эластичный; при 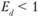 – неэластичный; при
– неэластичный; при  – единичный.
– единичный.