Модель роста с техническими изменениями
Эта модель становится более реалистичной при добавлении в уравнение фактора воздействия научно-технического прогресса (НТП) на рост производительности. Наиболее подходящий путь добавления НТП – рассмотрение технических знаний как отдельного самостоятельного фактора. Этот подход был развит в работах Роберта Солоу.
Историческая справка
Роберт Мертон Солоу (род. 1924) – лауреат Нобелевской премии 1987 г. "за фундаментальные исследования в области теории экономического роста". Учился в Гарвардском (где получил степень доктора философии) и Колумбийском университетах. Ветеран Второй мировой войны. Профессор Массачусетского технологического института. Президент Международной экономической ассоциации (1999–2002) и Эконометрического общества (1964), а также президент Американской экономической ассоциации в 1979 г. Автор макроэкономической модели, учитывающей вклад технологического параметра в экономический рост, которая известна в экономической теории как "модель Солоу".
В модели Р. Солоу и капитал, и рабочая сила выигрывают от технического прогресса, что отражено в следующем уравнении:
 (5.11)
(5.11)
где А – новые знания.
Технический прогресс в этой модели независим от затрат капитала или рабочей силы. Если необходимо учесть рост знаний, технический прогресс на протяжении какого-либо периода, то функция Кобба – Дугласа изменяется: добавляется дополнительная переменная, чтобы отразить влияние технического прогресса:
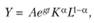 (5.12)
(5.12)
где A – постоянный уровень технического прогресса на определенном периоде времени t.
Данное уравнение показывает воздействие технического прогресса на рост выпуска в чрезвычайно упрощенном виде, так как игнорирует возможность проявления НТП в новых разработках оборудования. Рабочая сила тоже приобретает новый опыт и знания, которые повышают производительность, и в таком случае рабочую силу, так же как и капитал, необходимо ранжировать по качеству.
На рис. 5.4 показано влияние НТП на производительность труда.

Рис. 5.4. Влияние технического прогресса на производительность труда
Учитывая все вышесказанное, уравнение роста можно преобразовать следующим образом:
 (5.13)
(5.13)
где g – ежегодный рост технического прогресса.
Такая расширенная версия модели привлекает возможностью уверенного роста производительности труда в долгосрочной перспективе. Это легко заметить, добавляя  в обе части уравнения:
в обе части уравнения:
 (5.14)
(5.14)
Таким образом, даже если основной капитал и рабочая сила будут расти с той же самой скоростью, то производительность увеличится, если уровень технического прогресса превышает ноль. Долгосрочное равновесие возможно, если рост производительности и рост основного капитала будут равными ( ). В соответствии с уравнением (5.14), рост
). В соответствии с уравнением (5.14), рост  при росте капитала
при росте капитала  приведет к долгосрочному равновесному росту производительности:
приведет к долгосрочному равновесному росту производительности:
 (5.15)
(5.15)
Даже это краткое описание неоклассической модели роста демонстрирует основные факторы, определяющие региональные различия в производительности труда.
 (5.16)
(5.16)
где  объяснены выше; g – уровень еже годного НТП; r – регион.
объяснены выше; g – уровень еже годного НТП; r – регион.
Согласно этому уравнению, неоклассическая модель выделяет три причины диспропорций в развитии регионов:
1) уровень НТП;
2) рост размера капитала;
3) рост рабочей силы.
Уровень НТП  (для региона r) может отличаться по регионам, по крайней мере, в среднесрочной перспективе.
(для региона r) может отличаться по регионам, по крайней мере, в среднесрочной перспективе.
Выделяя рост рабочей силы  из двух половин уравнения, можно получить:
из двух половин уравнения, можно получить:
 (5.17)
(5.17)
Таким образом, региональные различия в росте производительности труда объясняются региональными различиями в уровне НТП и капиталовооруженности.