Модель Хольта и ее варианты

Модель Хольта соответствует модели ETS(A,A,N) или ETS(M,A,N). Сначала рассмотрим модель в базовой форме. Она имеет вид

(7.64)

Если попытаться дать интерпретацию предложенным Хольтом формулам, опираясь на уравнение линейного тренда, то сделать это будет нелегко. Поэтому, чтобы понять логику рассуждений Хольта, обратимся непосредственно к сути формул адаптации коэффициентов в (7.64). Коэффициент lt меняется во времени и либо растет, либо снижается (в зависимости от значений коэффициента bt), Это следует из первой формулы (7.64), в которой первое слагаемое характеризует достигнутый уровень возрастающего ряда, а второе – прирост этого уровня.

Необходимо обратить внимание на следующее. Если показатель уt измеряется, например, в рублях, то и коэффициент lt также измеряется в рублях. Из (7.64) следует, что коэффициент bt должен измеряться как скоростной параметр отношением руб/время. Поэтому непосредственно складывать коэффициент 4 и коэффициент bt, как это сделано во втором слагаемом правой части равенства второго уравнения в (7.64), нельзя, как нельзя складывать расстояние и скорость. Можно предполагать, что в скобках второго слагаемого второго равенства (7.64) коэффициент bt умножается па время h, которое в данном случае равно единице и поэтому в формулу нс включено. Только в этом случае размерности слагаемых совпадут, и можно будет произвести их сложение. Таким образом, время в модели Хольта не имеет точки отсчета, и его показатель h является приростным, причем расстояния между двумя соседними наблюдениями равны единице. Время в модели Хольта равномерно. Из этого следует, что модель (7.64) представляет собой нс общеизвестное уравнение тренда, а модель Naive с постоянным приростом:

(7.65)

Если рассматривать модель именно так, то смысл каждого равенства модели Хольта становится очевидным.

Вторая формула в системе (7.64), позволяющая вычислить адаптивное значение коэффициента lt, представляет собой модель Брауна, где первое слагаемое характеризует фактически достигнутый уровень ряда в момент времени ί, а второе – его расчетное значение в предыдущий момент. Иначе говоря, метод Брауна в этой ситуации применим к прогнозированию значений коэффициента lt.

Теперь легко понять смысл третьего уравнения модели Хольта (7.64). Первое слагаемое в нем представляет характеристику постоянного прироста модели (7.65), а второе – характеризует состояние коэффициента bt в предыдущий момент времени. Вновь методом Брауна прогнозируется значение коэффициента bt.

Заметим, в случае β*=α мы получаем модель, называющуюся моделью двойного сглаживания^[1].

В существующей теории и практике социально-экономического прогнозирования значения постоянных сглаживания ограничиваются пределами от 0 до 1. Если в модели Брауна, разработанной для прогнозирования некоторого изменяющегося во времени показателя, ограничения на постоянную сглаживания логично следовали из предпосылок самой модели, поскольку она представляла собой среднюю взвешенную ряда, то в модели Хольта (как и во многих других модификациях метода Брауна) такое ограничение из свойств модели не вытекает. Это возможно только в том случае, когда есть основания априорно предполагать, что коэффициенты линейного тренда меняются во времени относительно некоторого постоянного уровня и независимы друг от друга.

Прогнозист может предполагать, что на определенном промежутке времени значения коэффициентов модели меняются относительно некоторого своего уровня. Но независимость коэффициентов lt и bt не выполняется никогда: при расчете коэффициента lt используется значение коэффициента bt, а при вычислении коэффициента bt напрямую используется коэффициент lt. Поскольку каждый из коэффициентов вычисляется с помощью собственного значения постоянной сглаживания, получается, что постоянная сглаживания а влияет на постоянную сглаживания β и наоборот. Это говорит о том, что использование классических пределов на области изменения постоянных сглаживания в методе Хольта является необоснованным.

Истинные пределы, в которых лежат постоянные сглаживания для модели Хольта были выведены еще в 1968 г.^[2] и могут быть записаны в виде системы

(7.66)

В форме коррекции ошибок ограничение (7.66) принимает вид^[3]

(7.67)

Как видим из (7.67), постоянная сглаживания β лежит в пределах от 0 до 4 (в зависимости от значений а, лежащей в пределах от 0 до 2). Получение значений β > 1 может означать, что в исходном ряде данных происходят существенные изменения, которые модель Хольта не успевает описать. Возможно, в таком случае имеет смысл попытаться построить другую модель экспоненциального сглаживания (например, модель с мультипликативным трендом).

На данный момент никаких доказательство того, что ограничение постоянных сглаживания классическим промежутком увеличивает точность прогнозов модели, нет. Более того, прогнозы, получаемые по моделям с более широкими интервалами, в ряде случаев оказываются точнее прогнозов по моделям с интервалами от 0 до 1^[4]3.

Чтобы запустить модель по формуле (7.64), нужно каким-то образом задать стартовые значения параметрам l0 и b0. Обычно это делается автоматически во время нахождения значений оптимальных постоянных сглаживания. Однако в таком случае для запуска модели требуется подобрать четыре параметра: α, β, l0 и b0, что представляет собой нетривиальную задачу, так как во время подбора этих параметров исследователь, скорее всего, столкнется с несколькими локальными минимумами целевой функции. В таком случае рекомендуется, во-первых, рассчитать коэффициенты модели линейного тренда по всему ряду данных и взять полученные значения уровня ряда и угла наклона в качестве стартовых значений для l0 и b0, а во-вторых, – при подборе численными методами задать разные значения α и β, от которых осуществляется поиск, найти несколько локальных минимумов, после чего выбрать минимальный из них. Скорее всего, полученные значения будут характеризовать глобальный минимум целевой функции.

В качестве целевой функции, на основе которой происходит подбор параметров, обычно используют дисперсию ошибки (7.16), среднюю абсолютную ошибку (7.17) или отрицательное значение функции правдоподобия. Функцию правдоподобия применительно к подобным задачам мы рассмотрим в параграфе 7.7.

Посмотрим, какой прогноз дает модель Хольта при построении по ряду данных № 41, рассмотренному нами ранее. Построение модели мы осуществим в программе "R". Чтобы при построении модели использовать естественные границы (7.67) в функции ets нужно добавить параметр "bounds = “admissible”".

В результате расчетов мы получили следующие параметры модели:

α = 1,971; β = 0,058; l0 = 639,594; b0 = 274,022.

Как видим, оптимальная постоянная сглаживания для уровня ряда оказалась больше единицы, а для угла наклона – достаточно близкой к нулю. Это говорит о том, что в ряде данных происходят существенные изменения уровня, но угол наклона при этом изменяется незначительно. Тем не менее возможно, что использование другой прогнозной модели позволило бы получить более точные прогнозы ряда этих данных.

На рис. 7.13 показаны ряд данных № 41, модель Хольта и прогноз по ней.

Рис. 7.13. Аппроксимация ряда данных № 41 из базы М3 и его прогнозы на шесть наблюдений вперед моделью Хольта:

сплошная линия – фактические значения;

прерывистая – расчетные значения

Как видим, из-за смены тенденции на периоде с 1989 по 1994 г. модель Хольта дала не самый точный прогноз: sMAPE = 25,66%. Однако в случае сохранения линейных тенденций в ряде данных точность метода, конечно же, становится выше.

Построение модели Хольта на практических рядах данных привело прогнозистов к выводу о том, что на долгосрочной перспективе модель "перестреливает" фактические значения, т.е. в долгосрочной перспективе простая линейная тенденция не сохраняется, обычно рост фактических значений со временем замедляется. Чтобы учесть это и дать более точный прогноз, в модель Хольта был введен коэффициент демпфирования φ^[5]. Полученная модифицированная модель обозначается "ETS(A,Ad,N)" и имеет вид

(7.68)

Чтобы лучше понять смысл суммы в первом уравнении, обратимся к модели Хольта (7.64). Если расчетное значение на h шагов вперед в ней представить не через произведение коэффициента bt, на h, а через сумму b, h раз, то мы получим

Как видим, на каждом последующем шаге к полученному значению в модели Хольта просто прибавляется один и гот же коэффициент прироста bt.

В модели Хольта с демпфированием на каждом шаге коэффициент bt, прибавляемый к предыдущему уровню, умножается на φ в степени номера шага:

Если , то возведение его в степень с каждым шагом будет давать все меньшее число. В результате получается, что прирост с каждым последующим шагом становится все меньше, а тренд начинает затухать.

Что характерно, при φ = 1 мы получаем простую модель Хольта (7.64), а в случае, когда φ = 0, – модель Брауна (7.6).

Теоретически возможны ситуации, когда , но они не имеют практической ценности, так как тренд в таком случае уже не затухает, а:

• растет экспоненциально (в случае, если φ > 1);

• начинает колебаться вокруг прямой линии со все увеличивающейся амплитудой (в случае, если φ < -1);

• приводит к знакочередующемуся затухающему ряду , аналогично модели вида (5.38) с

Ограничения, накладываемые на постоянные сглаживания, в данном случае становятся еще более сложными^[6]:

(7.69)

Построив модель Хольта с демпфированным трендом на том же примере ряда №41, мы получили следующие параметры:

По ним уже можно сказать, что модель Хольта с демпфированным трендом не очень подходит для описания исходного ряда данных. Из-за того, что коэффициент демпфирования оказался равным единице, мы пришли к простой модели Хольта. Единственное, что отличает эту модель от модели, полученной в предыдущем случае, – это стартовые значения l0 и b0. Естественно, что прогноз, полученный в результате но этой модели, представляет собой простую прямую линию (рис. 7.14).

Рис. 7.14. Аппроксимация ряда данных № 41 из базы М3 и его прогнозы на шесть наблюдений вперед моделью Хольта с демпфированным трендом:

сплошная линия – фактические значения;

прерывистая – расчетные значения

Очевидно, что прогноз, полученный таким образом, оказался все так же неточен, как и в случае с моделью Хольта. Ошибка здесь оказалась даже выше, чем в прошлый раз: sMAPE = 26,01%.

Чтобы понять, чем же все-таки модель (7.68) отличается от модели (7.64), рассмотрим другой ряд данных – ряд № 42. Для него оптимальные постоянные значения коэффициентов получились следующими:

Стоит обратить внимание на то, что оптимальные постоянные сглаживания в данном случае не вписываются в классические пределы (0; 1). При этом прогноз по полученной модели получился таким, как показано на рис. 7.15, слева.

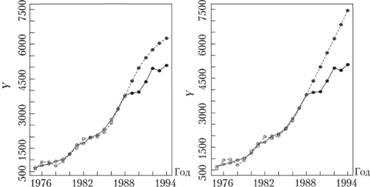
Рис. 7.15. Аппроксимация ряда данных № 42 из базы М3 и его прогнозы на шесть наблюдений вперед моделью Хольта с демпфированным трендом с ограничениями (7.69) (слева) и с классическими ограничениями (справа):

сплошная линия – фактические значения;

прерывистая – расчетные значения

Как видим, на этом ряде мы как раз столкнулись с ситуацией, когда тенденция на прогнозируемом промежутке изменилась и стала более пологой. Несмотря на то что прогноз оказался систематически завышенным, за счет демпфирования он сильно не задирается и постепенно приближается к фактическим значениям. Ошибка аппроксимации все же достаточно велика: sMAPE = 18,99%.

Если бы мы ограничили постоянные сглаживания классическим промежутком, то получили бы другие коэффициенты модели (с легко интерпретируемыми постоянными сглаживания):

что привело бы к совершенно другому прогнозу (рис. 7.15, справа).

Видно, что классические ограничения, наложенные во втором случае, привели к получению завышенного коэффициента демпфирования, что в результате дало более задирающийся прогноз, чем в случае с ограничениями (7.69): sMAPE = 22,91%.