Модель экономически выгодных размеров заказываемых партий
Рассмотрим работу склада, на котором хранятся товарные запасы, расходуемые на снабжение потребителей. Работа реального склада сопровождается множеством отклонений от идеального режима: заказана партия одного объема, а прибыла партия другого объема; но плану партия должна прибыть через две недели, а она пришла через 10 дней; при норме разгрузки одни сутки разгрузка партии длилась трое суток и т.д. Учесть все эти отклонения практически невозможно, поэтому при моделировании работы склада обычно делаются следующие предположения:
– скорость расходования запасов со склада – постоянная величина, которую обозначим М (единиц товарных запасов в единицу времени); в соответствии с этим график изменения величины запасов в части расходования является отрезком прямой;
– объем партии пополнения Q есть постоянная величина, так что система управления запасами – это система с фиксированным размером заказа;
– время разгрузки прибывшей партии пополнения запасов мало, будем считать его равным нулю;
– время от принятия решения о пополнении до прихода заказанной партии есть постоянная величина At, так что можно считать, что заказанная партия приходит как бы мгновенно: если нужно, чтобы она пришла точно в определенный момент, то ее следует заказать в момент времени на At ранее;
– на складе не происходит систематического накопления или перерасхода запасов. Если через Т обозначить время между двумя последовательными поставками, то обязательно выполнение равенства: Q = МТ. Из сказанного выше следует, что работа склада происходит одинаковыми циклами длительностью Т и за время цикла величина запаса изменяется от максимального уровня S до минимального уровня s;
– наконец, будем считать обязательным выполнение требования, чтобы отсутствие запасов на складе было недопустимым, т.е. выполняется неравенство s ≥ 0. С точки зрения уменьшения издержек склада на хранение отсюда вытекает, что s = 0 и, следовательно, S = Q.
Окончательно график "идеальной" работы склада в форме зависимости величины запасов у от времени t будет иметь вид, представленный на рис. 8.12.

Рис. 8.12
В предыдущем параграфе отмечалось, что эффективность работы склада оценивается по его затратам на пополнение запасов и их хранение. Расходы, не зависящие от объема партии, называют накладными. Сюда входят почтово-телеграфные расходы, командировочные, некоторая часть транспортных расходов и др. Накладные расходы будем обозначать через К. Издержки хранения запасов будем считать пропорциональными величине хранящихся запасов и времени их хранения. Издержки на хранение одной единицы запасов в течение одной единицы времени называются величиной удельных издержек хранения; мы их будем обозначать через h.
При изменяющейся величине хранящихся запасов издержки хранения за некоторое время Т получают путем умножения величины h-T па среднее значение величины запасов в течение этого времени Т. Таким образом, затраты склада за время Т при размере партии пополнения Q в случае идеального режима работы склада, представленного на рис. 8.12, равны

После деления этой функции на постоянную величину Т с учетом равенства Q = МТ получим выражение для величины затрат на пополнение и хранение запасов, приходящихся на единицу времени:
 (8.38)
(8.38)
Это и будет целевой функцией, минимизация которой позволит указать оптимальный режим работы склада.
Найдем объем заказываемой партии Q, при котором минимизируется функция средних затрат склада за единицу времени, т.е. функция  . На практике величина Q часто принимает дискретные значения, в частности, из-за использования транспортных средств определенной грузоподъемности; в этом случае оптимальное значение Q находят перебором допустимых значений Q. Мы будем считать, что ограничений на принимаемые значения Q нет, тогда задачу на минимум функции
. На практике величина Q часто принимает дискретные значения, в частности, из-за использования транспортных средств определенной грузоподъемности; в этом случае оптимальное значение Q находят перебором допустимых значений Q. Мы будем считать, что ограничений на принимаемые значения Q нет, тогда задачу на минимум функции  (легко показать, что она является выпуклой (рис. 8.13)) можно решить методами дифференциального исчисления:
(легко показать, что она является выпуклой (рис. 8.13)) можно решить методами дифференциального исчисления:

откуда находим точку минимума Qопт:
 (8.39)
(8.39)
Эта формула называется формулой Уилсона (по имени английского ученого-экономиста, получившего ее в 20-х годах прошлого столетия).
Оптимальный размер партии, рассчитываемый по формуле Уилсона, обладает характеристическим свойством: размер партии Q оптимален тогда и только тогда, когда издержки хранения за время цикла Т равны накладным расходам К.
Действительно, если  , то издержки хранения за цикл равны
, то издержки хранения за цикл равны

Если же издержки хранения за цикл равны накладным расходам, т.е.

то

Проиллюстрируем характеристическое свойство оптимального размера партии графически (рис. 8.13).
На рис. 8.13 видно, что минимальное значение функции Z1(Q) достигается при том значении Q, при котором равны значения двух других функций, ее составляющих.
Используя формулу Уилсона (8.39), в сделанных ранее предположениях об идеальной работе склада можно получить ряд расчетных характеристик работы склада в оптимальном режиме: оптимальный средний уровень запаса
 (8.40)
(8.40)
оптимальная периодичность пополнения запасов
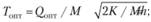 (8.41)
(8.41)

Рис. 8.13
оптимальные средние издержки хранения запасов в единицу времени
 (8.42)
(8.42)
Пример 8.5. Рассмотрим типовую задачу. На склад доставляют цемент на барже по 1500 т. В сутки со склада потребители забирают 50 т цемента. Накладные расходы по доставке партии цемента равны 2 тыс. руб. Издержки хранения 1 т цемента в течение суток равны 0,1 руб. Требуется определить: 1) длительность цикла, среднесуточные накладные расходы и среднесуточные издержки хранения; 2) эти же величины для размеров партии в 500 т и в 3000 т; 3) каковы оптимальный размер заказываемой партии и расчетные характеристики работы склада в оптимальном режиме.
Решете. Параметры работы склада: М = 50 т/сут.; К =2 тыс. руб.; h = 0,1 руб./т • сут.; Q = 1500 т.
1. Длительность цикла:
Т= Q : М = 1500 т : 50 т/сут. = 30 сут.; среднесуточные накладные расходы:
К: T = 2 тыс. руб.: 30 сут. !!!* 67 руб./сут.; среднесуточные издержки хранения: h • Q/2 = 0,1 руб./т • сут. • 1500 т/2 = 75 руб./сут.
2. Аналогичные расчеты проведем для Q1 = 500 т:
Т1 = Q1 : M = 500 т : 50 т/сут. = 10 суг.;
К: Т1= 2 тыс. руб.: 10 сут. = 200 руб./сут.; h • Q1/2 = 0,1 руб./т • сут • 500 т/2 = 25 руб./сут.
и для Q2 = 3000 т:
Т2 = Q2 : M = 3000 т : 50 т/сут. = 60 сут.
К : Т2 = 2 тыс. руб.: 60 сут. = 33 руб./сут.;
h • Q2/2 = 0,1 руб./т • сут. • 3000 т/2 = 150 руб./сут.
3. Найдем оптимальный размер заказываемой партии по формуле Уилсона (8.39):

оптимальный средний уровень запаса по формуле (8.40):

оптимальную периодичность пополнения запасов по формуле (8.41):

оптимальные средние издержки хранения запасов в единицу времени по формуле (8.42):
