Модель экономических показателей (Э-модель)

Стохастические модели оценки риска (достоверности) стоимостных курсов валюты (процесса инфляции), финансовых элементов (опционов), инвестиционных показателей (оценки доходности или убыточности) портфеля (валют, компонентов разных фирм) – модификация моделей БШ американского опциона типа "колл" с использованием интеграла ошибок. Как известно [38], стоимость американского опциона типа "колл" вычисляется по формуле Блэка – Шоулза, в состав которой входят два типа риска – ставка без риска r и волатильность (изменчивость) σa. Изменение σa во времени t носит случайный характер, поскольку цена актива определяется случайными изменениями текущей цены базового актива x(t).

Текущая цена базового актива определяет прибыльность или убыточность покупки опциона инвестором-финансистом-аналитиком фондовой биржи, а следовательно, и эффективность его портфеля опционов. Вот почему важно установить формулы для оценки вероятности прибыльности R(t) или убыточности F(t) покупки опциона, поскольку формула Блэка – Шоулза этого не учитывает, что ограничивает область ее применения в России.

Обобщенный процесс изменения текущей цены базового актива х(t) опциона может быть аппроксимирован непрерывным марковским процессом диффузионного типа, подчиняющимся стохастическому дифференциальному уравнению первого порядка типа И то (см. (4.10)):

где A(t) – детерминированная функция, характеризующая изменение среднего значения (скорость, коэффициент сноса) текущей цены базового актива; B(t) – детерминированная функция, характеризующая изменение дисперсии (коэффициент диффузии) текущей цены базового актива; η(t) – случайная составляющая гауссовского типа.

Для текущей цены базового актива выражение для функции распределения времени до первого изменения цены (первого достижения предельного уровня изучаемым процессом) вид функций A(t) и B(t) конкретизируется. Процесс изменения текущей цены базового актива (имеется в виду совокупность однотипных цен) рассматривается как однородный, т.е. с постоянной средней скоростью и постоянным средним квадратическим отклонением скорости (или постоянным коэффициентом вариации скорости). В таком случае уравнение процесса записывается в виде формулы (4.10) [37]:

где а – коэффициент сноса; b – коэффициент диффузии (b2 – средняя скорость изменения дисперсии текущей цены базового актива).

Поскольку марковский процесс диффузионного типа определяется уравнением вида (4.10), то диффузия условной переходной плотности вероятности λ(t0, x0; t, x) цены актива этого процесса выражается уравнением Фоккера – Планка – Колмогорова (4.11).

Известно, что плотность распределения времени достижения границы изучаемым процессом – плотность распределения времени до изменения цены f(t) – связана с условной плотностью вероятности перехода процесса из одного состояния в другое выражением (4.12). Чтобы для текущей цены базового актива определить плотность распределения времени до изменения цены f(t), необходимо получить выражение для λ(t0, x0; t, х), решив уравнение (4.12), после чего найти частную производную по времени от функции λ(t0, х0; t, х) и полученное выражение проинтегрировать по параметру х.

Примечания. 1. Рассмотренная схема формализации принята для так называемых диффузионных распределений.

2. Выражение для закона распределения вытекает из решения уравнения диффузии вероятностей. Непрерывный марковский процесс был использован для построения вероятностной модели диффузии и назван диффузионным процессом.

Уравнение (4.11) представляет собой параболическое дифференциальное уравнение в частных производных. Для решения уравнений такого тина необходимо установить краевые (граничные) условия, которые для текущей цепы базового актива определяются из общих соображений о процессе и искомой функции.

Начальные условия в общем случае, исходя из искомой функции λ(t0, х0; t, х) (плотности вероятностей), могут быть заданы в виде

(4.30)

где λ(x0) – некоторое произвольное распределение текущей цены базового актива в начальный момент.

Если начальное значение параметра х задано (можно положить x'0 = 0, t0 = 0), то λ0(x0) вырождается в δ-функцию (4.13).

Для текущей цены базового актива для определения граничных условий необходимо оценить характер реализаций процесса х(С). Первое достижение реализацией границы заданной области (в нашем случае параметр х нормирован и изменяется от нуля до единицы) соответствует изменению текущей цены базового актива опциона. По характеру изменения реализации необходимо определить, моделирует ли изменение цены первое достижение реализацией границы заданной области и может ли реализация повлиять на изучаемый процесс x(t) (и соответственно на искомую функцию λ(x, t)) в дальнейшем, после первого достижения границы.

В случае, когда реализация имеет немонотонный характер, после первого достижения границы заданной области (это соответствует изменению цены актива опциона) она может снова возвратиться в заданную область и участвовать в наблюдаемом процессе. Для того чтобы первое достижение границы немонотонной реализацией моделировало изменение цепы и дальнейшая реализация не участвовала в наблюдаемом процессе и не влияла на λ(t, х), на границе заданной области ставится граничное условие типа поглощающего экрана. В случае его постановки любая реализация, впервые достигнув его, навсегда останется на границе, вне заданной области.

Поскольку рассматриваемые реализации процесса изменения текущих цен базового актива имеют немонотонный характер (что характерно для России), в качестве граничных при решении уравнения (4.11) можно принять условия (4.14), (4.15).

Граничное условие (4.14) чисто формально. Поскольку изучаемый процесс (текущая цена базового актива) не может принимать отрицательные значения, установленная левая граница является недостижимой (естественной) и никак не влияет на процесс в заданной области. Принятие формального условия (4.14) необходимо для решения уравнения (4.11). Граничное условие (4.15) вытекает из приведенных соображений и соответствует поглощающему экрану в точке х= 1.

Решение уравнения (4.11) для краевых (граничных) условий (4.13)-(4.15) записывается в следующем виде:

(4.31)

После дифференцирования равенства (4.31) по времени получается выражение

подстановка которого в (4.12) и интегрирование приводят к уравнению плотности распределения времени до первого изменения цены актива

Далее так же, как описывалось выше, представим последний интеграл в виде суммы интегралов J1 + J2 и получим компактное выражение для плотности распределения времени до первого изменения цены [311

где

Проведя аналогичную рассмотренной выше подстановку для определения первого интеграла и учитывая граничные условия, как и ранее, после преобразований получим

Произведя обратную замену переменных, имеем

Для второго интеграла имеем

После суммирования J1 и J2 и сокращения на 2 числителя и знаменателя выражение для плотности распределения времени до первого изменения цены принимает вид

(4.32)

Для однородного процесса деградации диффузионного типа коэффициент диффузии имеет простую связь с обычно используемыми характеристиками процесса – средним квадратическим отклонением скорости процесса σ и коэффициентом вариации процесса ν:

(4.33)

С учетом соотношения (4.33) выражение для закона распределения времени до первого изменения цепы (DN-распределение) получится в следующем виде:

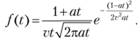(4.34)

Плотности (4.34) соответствует функция распределения

где – нормированная функция Лапласа (интеграл вероятности).

Математическое ожидание и дисперсия времени до первого изменения цены равны соответственно Из этих соотношений коэффициент вариации распределения времени до первого изменения цены равен коэффициенту вариации процесса изменения цены:Коэффициенты асимметрии и эксцесса определяются из выражений

Оценка вероятности доходности опциона с учетом изменений текущей цены базового актива. Используем здесь тот же аппарат, что и при вычислении интенсивности отказов для ZW-ΦΡ. Поскольку

(4.35)

где v – коэффициент вариации текущей цены базового актива;

(4.36)

– нормированная функция Лапласа, то интенсивность изменений λ(ί) текущей цены базового актива определяется как [31]:

Отсюда средний срок до изменения цены:

Проведя преобразование функции Лапласа (4.36) через функцию ошибок erf(z), получим

(4.37)

где

Полагая v = 0,707 (значения этого показателя для текущей цены базового актива опциона оценим в интервале от 0,7 до 1,2) и используя формулы (4.35) и (4.37), получим модель, удобную для вычислений вероятности доходности опциона:

Соответствующая модель для вычислений вероятности убыточности американского опциона будет иметь вид

(4.38)

Эффективность портфеля должна быть максимальной, что может быть записано в форме

Пример 4.12

Оценить эффективность портфеля по вероятности доходности опциона с тремя типами акций (валют) – "храните яйца в разных корзинах". Исходные данные представлены на рис. 4.14.

Рис. 4.14. Структура портфеля опционов:

количество акций 1-го вида k = 12; количество акций 2-го вида n ≥ 10; количество акций 3-го вида m ≥ 100; l – число заказов в портфеле

Решение

Эффективности трех составных частей портфеля опционов американского типа, вычисленные по формуле (4.38), на 10-летний срок исполнения (87 600 ч) сведены в табл. 4.7.

Таблица 4.7

Результаты расчета

Rj(t) (для составляющих частей портфеля акций i = 1, 2, 3)	λ„ 1/ч
R1(t) = 0,99572	1,73• 10-6
R2(t) = 0,999573	12,5• 10-7
R3(t) = 0,999996	8 • 10-7

Эффективность портфеля:

Э(t)=Ri(t)R2(t)R3(t)= 0,99572 0,999573 0,999996 0,995290846.

Итак, на основе теории случайных процессов и использования дифференциального стохастического уравнения Ито получены формулы и проведены расчеты по оценке эффективности портфеля активов при участии в опционе американского типа в условиях России.