Модель домохозяйства
Домохозяйство в модели Алонсо распределяет свой доход у между расходами на транспорт k(t), которые зависят от расстояния до центра города t, расходами на землю площадью q и расходами на остальные товары и услуги 2, причем постулируется, что цена земли Р(t) за единицу площади снижается (так оно обычно и бывает в реальных городах) по мере удаления от центра города (рис. 2.27). Тогда бюджетное ограничение домохозяйства имеет следующий вид:
 (2.3)
(2.3)
Переменные выбора: z, q и t. Остальные переменные домохозяйство менять не может. Чтобы изобразить бюджетное ограничение в трехмерном пространстве, можно исследовать его проекции на каждую из координатных плоскостей.

Рис. 2.27. Функция цен на землю в зависимости от расстояния до центра города
Сначала зафиксируем расстояние до города  . Тогда (2.3) можно записать так:
. Тогда (2.3) можно записать так:
 (2.4)
(2.4)
Так как отношение цены на прочие товары к цене на землю на заданном расстоянии – константа, имеем на графике прямую линию (рис. 2.28).

Рис. 2.28. Множество выбора между q и z при фиксированном t = t0
Аналогично зафиксируем z = z0. Тогда бюджетное ограничение (2.3) можно записать так:
 (2.5)
(2.5)
Если принять гиперболическую форму функции цены на землю (рис. 2.29) и близкую к параболической форму функции затрат на транспорт k(t), то на графике такое ограничение будет выглядеть как кривая (рис. 2.29). Объяснить ее можно следующим образом: по мере удаления от центра издержки на транспорт k(t) будут медленно увеличиваться и оставлять в бюджете все меньше денег на аренду земли q. Но цена земли за единицу площади P(t) будет быстро уменьшаться с расстоянием от центра так, что домохозяйство сможет арендовать земельный участок все большей площади q даже после уплаты возросших транспортных расходов. Однако когда расстояние от центра становится очень большим, цена на землю начинает падать слишком медленно, а издержки на транспорт расти слишком быстро, что ведет к снижению доступной для домохозяйства площади. Заметим, что селиться на убывающей части параболы на рис. 2.29 не имеет смысла.

Рис. 2.29. Множество выбора между q и t при фиксированном z = z0
Теперь зафиксируем q = q0. Тогда (2.4) можно записать так:
 (2.6)
(2.6)
Это ограничение также выглядит как кривая (рис. 2.30). При фиксированной площади участка домохозяйство будет экономить средства при переезде дальше от центра. При небольшом удалении от центра этой экономии будет хватать на покрытие роста расходов на транспорт так, что еще остается на увеличение потребления прочих товаров z. Однако на очень большом расстоянии экономия исчезает и рост расходов на транспорт приходится компенсировать снижением потребления прочих товаров.

Рис. 2.30. Множество выбора между z и t при фиксированном q = q0
В итоге бюджетное ограничение будет выглядеть как на рис. 2.31.

Рис. 2.31. Бюджетное ограничение домохозяйства в модели Алонсо
Далее нам нужно определить функцию полезности домохозяйства, которую оно будет максимизировать на данном бюджетном ограничении, выбирая z, q и t. Так как функция будет также трехмерной, Алонсо снова предлагает определить ее проекции при фиксированном уровне полезности, т.е. кривые безразличия.
Начнем с z = z0. В модели предполагается, что члены домохозяйства должны периодически посещать центр города по работе, для осуществления покупок и для развлечения. При этом путешествие доставляет им дискомфорт хотя бы потому, что оно занимает время. Тогда при удалении жилья от центра, чтобы полезность домохозяйства оставалась постоянной, площадь его участка должна увеличиваться (помним, что 2 фиксировано), как показано на рис. 2.32.
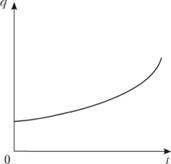
Рис. 2.32. Кривая безразличия между q и t при фиксированном r=r0
В отличие от рис. 2.29, где изображена проекция бюджетного ограничения, здесь изображена проекция трехмерной плоскости безразличия. Иными словами, при фиксированном 2, домохозяйство будет получать одинаковую полезность от любой точки на кривой рис. 2.32. Эта кривая вогнута потому, что Алонсо предположил ее вогнутой, т.е. предположил, что домохозяйства испытывают неудобства от езды и поэтому потребуют возрастающей компенсации за удаление от центра в виде дополнительной площади земельного участка q при фиксированном z.
Теперь зафиксируем расстояние до центра t = t0. Размер участка и остальное потребление ведут себя как обычные товары-заменители (рис. 2.33).

Рис. 2.33. Кривая безразличия между q и г при фиксированном z = z0
При q = q0, как и в случае с фиксированным z, с увеличением расстояния от центра домохозяйству потребуется компенсация в виде увеличения потребления прочих товаров и услуг. Причем чем дальше будет уезжать домохозяйство, тем бо́льшую компенсацию оно захочет, т.е. функция неудобства от езды – возрастающая (рис. 2.34).

Рис. 2.34. Кривая безразличия между z и t при фиксированном
В итоге имеем плоскость безразличия при некотором фиксированном уровне полезности на рис. 2.35. Оптимальный вектор (z, q, t) определится в точке касания плоскостей бюджетного ограничения и плоскости безразличия при максимально возможном уровне полезности.

Рис. 2.35. Плоскость безразличия между z, t и q в модели Алонсо
Найдем теперь аналитическое решение задачи максимизации полезности домохозяйства при бюджетном ограничении  . Цена композитного товара
. Цена композитного товара  задана экзогенно, так же как и функция цены земли в зависимости от расстояния до центра
задана экзогенно, так же как и функция цены земли в зависимости от расстояния до центра  и функция стоимости перемещения
и функция стоимости перемещения  . Решение – вектор неотрицательных значений
. Решение – вектор неотрицательных значений  , дающий максимальную полезность при бюджетном ограничении.
, дающий максимальную полезность при бюджетном ограничении.
Задача легко решается методом множителей Лагранжа:
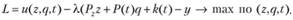 (2.7)
(2.7)
Необходимое условие экстремума (предполагается строгая выпуклость функции полезности, поэтому это условие будет и достаточным):
 (2.8)
(2.8)
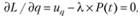 (2.9)
(2.9)
 (2.10)
(2.10)
 (2.11)
(2.11)
Решая систему, получаем следующие условия оптимума:
 (2.12)
(2.12)
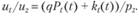 (2.13)
(2.13)
Интерпретация этих уравнений стандартна для микроэкономики: формула (2.13) показывает, что предельная норма замещения размера участка q композитным товаром z равна отношению их цен. Уравнение (2.13) показывает, что предельная норма замещения удаленности от центра t композитным товаром z равна отношению предельного изменения издержек на землю и транспорт к цене композитного товара г. Если домохозяйство, например, увеличивает удаленность от центра, уменьшаются расходы на аренду земли, но увеличиваются издержки на передвижение. Так как мы предположили, что домохозяйство не любит далеко ездить  и по определению прочих товаров
и по определению прочих товаров  , то в оптимуме из (2.13) имеем
, то в оптимуме из (2.13) имеем  . В свою очередь
. В свою очередь  (расходы на транспорт имеют форму параболы) и поэтому должно выполняться
(расходы на транспорт имеют форму параболы) и поэтому должно выполняться 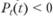 (цена на землю снижается с удалением от центра). Если же цена земли с удалением от центра возрастает, все домохозяйства будут селиться только в центре и город схлопнется в "черную дыру".
(цена на землю снижается с удалением от центра). Если же цена земли с удалением от центра возрастает, все домохозяйства будут селиться только в центре и город схлопнется в "черную дыру".
Также отметим, что неравенство 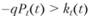 гарантирует, что при удалении от центра экономия на более дешевой земле превышает денежные потери от более длительных путешествий в центр, что требуется для компенсации дополнительного дискомфорта (отрицательной предельной полезности) от этих путешествий.
гарантирует, что при удалении от центра экономия на более дешевой земле превышает денежные потери от более длительных путешествий в центр, что требуется для компенсации дополнительного дискомфорта (отрицательной предельной полезности) от этих путешествий.
Теперь нам нужно найти функцию Bid-price группы домохозяйств. Как мы помним, у Тюнена была функция Bid-rent, которая показывала, какую максимальную ренту готовы платить фермеры за единицу площади земли при заданном удалении от города, при этом максимальная рента соответствовала отсутствию экономической прибыли фермера. Однако у домохозяйств нет прибыли, поэтому Алонсо вводит функцию Bid-price, которая показывает, какую максимальную ренту готово платить домохозяйство при заданном уровне полезности и разном удалении от города. Другими словами, это набор векторов цен на землю и расстояний от центра, между которыми потребитель безразличен. Тогда, очевидно, у разных людей будут разные функции Bid-price, и даже у одного человека будет множество функций, соответствующих разному уровню полезности.
Найти функцию Bid-price можно, решив задачу, обратную той, что мы уже решили, а именно задачу минимизации расходов при заданном уровне полезности:
 (2.14)
(2.14)
Тогда p,(t) – функция Bid-price домохозяйства i при условии, что оно тратит весь свой доход у. Как известно, решение данной задачи совпадает с решением прямой задачи, а именно:
 (2.15)
(2.15)
 (2.16)
(2.16)
При этом при нахождении  мы принимаем
мы принимаем 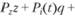

Заметим, что наклон функции  равен
равен 
 , так что готовность платить за землю уменьшается с удалением от города при фиксированном доходе и уровне полезности. То есть, чтобы полезность оставалась постоянной при движении от центра, потребители должны сберегать деньги на цене земли, чтобы компенсировать потери и рост дискомфорта от более длинных путешествий в центр. Заметим также, что в точке оптимума выполняется равенство
, так что готовность платить за землю уменьшается с удалением от города при фиксированном доходе и уровне полезности. То есть, чтобы полезность оставалась постоянной при движении от центра, потребители должны сберегать деньги на цене земли, чтобы компенсировать потери и рост дискомфорта от более длинных путешествий в центр. Заметим также, что в точке оптимума выполняется равенство  , т.е. кривая рыночной цены на землю и Bid-price соприкасаются. Слева от этой точки
, т.е. кривая рыночной цены на землю и Bid-price соприкасаются. Слева от этой точки 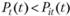 , т.е. домохозяйство предпочтет удалиться от центра, а справа – наоборот.
, т.е. домохозяйство предпочтет удалиться от центра, а справа – наоборот.
Однако наша конечная цель – найти равновесие на рынке земли, т.е.  при условии, что на границе города городская рента равна функции Bid-rent сельского хозяйства, и вся городская земля используется.
при условии, что на границе города городская рента равна функции Bid-rent сельского хозяйства, и вся городская земля используется.
Процесс определения  , предлагаемый Алонсо, представлен на рис. 2.36. Пусть сельское хозяйство имеет Bid-rent функцию Pag(t). Также предположим, что Bid-price функции домохозяйств имеют разный, но больший угол наклона, чем у Bid-rent фермеров. Но у каждого домохозяйства есть множество кривых Bid-price, соответствующих разным уровням полезности. Какие же из них будут определять цену реальной сделки? Посмотрим на домохозяйство с самой плоской кривой Bid-price: оно будет размещаться на самой границе города. Причем там оно согласится находиться только, если его полезность будет не ниже, чем при дальнейшем удалении от города за точку
, предлагаемый Алонсо, представлен на рис. 2.36. Пусть сельское хозяйство имеет Bid-rent функцию Pag(t). Также предположим, что Bid-price функции домохозяйств имеют разный, но больший угол наклона, чем у Bid-rent фермеров. Но у каждого домохозяйства есть множество кривых Bid-price, соответствующих разным уровням полезности. Какие же из них будут определять цену реальной сделки? Посмотрим на домохозяйство с самой плоской кривой Bid-price: оно будет размещаться на самой границе города. Причем там оно согласится находиться только, если его полезность будет не ниже, чем при дальнейшем удалении от города за точку  . То есть собственник земли в любой точке t не может назначить цену выше
. То есть собственник земли в любой точке t не может назначить цену выше  при уровне полезности, который получит домохозяйство, располагаясь в точке /;3 и платя ренту
при уровне полезности, который получит домохозяйство, располагаясь в точке /;3 и платя ренту  , равную ренте, которую готовы платить фермеры за расположение в этой точке. Так как предложение земли ограниченно, а спрос – не ограничен, Алонсо предполагает, что собственник земли сможет назначить максимально возможную цепу на свой участок, а именно
, равную ренте, которую готовы платить фермеры за расположение в этой точке. Так как предложение земли ограниченно, а спрос – не ограничен, Алонсо предполагает, что собственник земли сможет назначить максимально возможную цепу на свой участок, а именно

Аналогично, домохозяйство со следующим по значению углом наклона кривой Bid-price станет располагаться сразу же перед предыдущим домохозяйством и будет платить  . Каждая из Bid-price функций также задает размер участка, который займет домохозяйство при заданном расстоянии до центра и цене на землю. Равновесие наступит, когда вся земля в радиусе t3 вокруг центра будет занята домохозяйствами. Если какая-то земля останется пустой, то рынок уменьшит
. Каждая из Bid-price функций также задает размер участка, который займет домохозяйство при заданном расстоянии до центра и цене на землю. Равновесие наступит, когда вся земля в радиусе t3 вокруг центра будет занята домохозяйствами. Если какая-то земля останется пустой, то рынок уменьшит  так, чтобы заполнить этот пробел.
так, чтобы заполнить этот пробел.

Рис. 2.36. Определение цен сделки для нескольких домохозяйств