Модель Диксита – Стиглица – Кругмана

Прежде чем изложить пространственный вариант модели Диксита – Стиглица – Кругмана (в том виде, в каком она дана в известной книге Фуджиты, Кругмана и Венаблса), рассмотрим изначальную модель без пространства Диксита – Стиглица, впервые опубликованную в их статье 1977 г.

Как известно, в микроэкономике конкурентных рынков цена в равновесии равна предельным издержкам производства. Однако при наличии фиксированных издержек и соответствующей экономии от масштаба такие цены ведут к отрицательной прибыли, т.е. равновесие исчезает.

Для существования равновесия требуется разрешить фирмам иметь некоторую монопольную власть, которая позволит поддерживать цены выше предельных издержек, чтобы как минимум покрыть фиксированные расходы. Если последние не очень велики относительно размеров рынка, и рынок позволяет содержать несколько фирм, встает вопрос: какое их количество будет максимизировать общественное благосостояние?

Ответ зависит от того, как устроены предпочтения потребителей. Если люди безразличны к количеству разновидностей товаров, то оптимально наладить производство одной разновидности на одной фирме, так как в этом случае общие издержки на производство любого заданного количества товара будут минимальны. Однако в реальности люди очень различны и сильно отличаются в своих предпочтениях. Если их моделировать как одинаковых потребителей, то нужно разрешить им получать полезность от наличия выбора среди разновидностей одного и того же товара. В этом случае оптимальное число фирм может оказаться больше одной. Но как построить модель такого рынка в рамках микроэкономической теории?

Диксит и Стиглиц предложили наиболее простой и понятный способ. Они обратили внимание на то, что кривые и плоскости безразличия в микроэкономических моделях уже обычно задаются выпуклыми. Это значит, что если потребитель безразличен между единицей одного товара и единицей другого, он всегда предпочтет любому из них набор по половине единицы каждого. Тогда уровень полезности от набора будет зависеть от значения эластичности замещения между этими товарами. Чем она больше, тем больше полезность от набора, и наоборот. А значит, и оптимальное число фирм на рынке будет зависеть от эластичности замещения и, разумеется, от размера фиксированных издержек фирм.

Задача потребителя

Пусть все потребители в модели одинаковы, потребляют всего два вида товаров и имеют предпочтения формы Кобба – Дугласа:

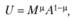(6.2)

где А – потребление агрегированного сельскохозяйственного товара, который можно условно назвать "продукты питания"; М – подфункция полезности от потребления промышленных товаров, или индекс потребления этих товаров; – постоянная доля каждого вида товаров в бюджете потребителей. Всего на рынке существует п разновидностей промышленных товаров, каждая потребляется в объеме , где i – номер разновидности товара. Предпочтения относительно промышленных товаров описываются функцией с постоянной эластичностью замещения (CES):

(6.3)

Условие обеспечивает выпуклость кривых безразличия для любых двух разновидностей товаров, так что при прочих равных условиях полезность потребителя будет тем выше, чем больше разновидностей товаров он потребляет.

Параметр р определяет степень заменяемости двух любых разновидностей друг другом в глазах потребителя. Если ρ равно единице, то М превращается в аддитивную функцию, заменяемость разновидностей полная, т.е. потребителю все равно, потреблять набор товаров или соответствующее количество одного из них. Когда же р близко к нулю, заменяемость минимальна, а полезность от разнообразия максимальна.

Что касается промышленных товаров длительного пользования, то заменяемость, например, холодильников различных марок, будет довольно высокой благодаря схожести их функций. Но так как все люди различаются в своих предпочтениях, они будут выбирать разные холодильники из-за небольших различий в дизайне, использованных материалах, габаритах и просто случайно.

Вопрос заменяемости разновидностей может быть интересен и на индивидуальном уровне для часто используемых товаров и услуг. Представьте себе двух людей: один ест только дешевые сосиски и все свободное время смотрит телевизор. Для него заменяемость всех доступных его бюджету видов питания полная, поэтому он покупает самую дешевую еду. Аналогично он заменил все виды доступных ему удовольствий на телевизор. В противоположность этому потребителю представим теперь человека, который каждый день предпочитает есть разные продукты и меняет способы их приготовления, часто выезжает на природу, занимается спортом и другими способами разнообразит свой досуг. У такого человека р для разновидностей питания и удовольствий будут близки к нулю.

Для удобства определим эластичность замещения между разновидностями промышленных товаров как

Бюджетное ограничение потребителя выглядит так:

(6.4)

где – цена единицы продуктов питания, – цена единицы промышленного товара разновидности i, а Y – доход потребителя, который максимизирует полезность (6.2) на ограничении (6.4).

Решается эта задача следующим образом. Во-первых, находим условие минимизации издержек на промышленные товары при заданном уровне полезности М и ценах :

(6.5)

Условие первого порядка для задачи (6.5) дает равенство предельной нормы замещения отношению цен на соответствующие товары:

(6.6)

Выражая отсюда m(i) и подставляя в ограничение , получим компенсированный спрос, или спрос Хикса:

(6.7)

Тогда суммарные оптимальные расходы на промышленные товары будут равны

(6.8)

Если теперь вспомнить, что М также можно считать индексом потребления промышленных товаров, т.е. аналогом их количества, то можно считать индексом цен на промышленные товары, так что их произведение дает суммарные расходы на упомянутые товары. G также показывает минимальные издержки покупки единицы индекса потребления М. Подставляя > в (6.8), получим и компенсированный спрос:

(6.9)

Теперь полную задачу максимизации полезности потребителя можно записать как

при (6.10)

Из курса микроэкономики можно вспомнить, что максимум полезности достигается при . Используя результаты первого шага, мы получаем функции некомпенсированного спроса на продукты питания и промышленные товары:

(6.11)

Заметим, что эластичность спроса на промышленные товары по цене равна а при фиксированном G, что вполне реалистично при большом количестве разновидностей.

Теперь мы можем исследовать максимизированную полезность потребителя:

(6.12)

Агрегированный индекс цен отражает стоимость жизни для потребителя. Заметим также, что увеличение числа доступных разновидностей п снижает этот индекс, и эго несмотря на то, что цены на отдельные разновидности p(j) не меняются. Дело в том, что при росте п бюджет делится на большее число товаров, а значит, каждый из них потребляется в меньшем количестве. Учитывая, что кривые безразличия выпуклые, снижение потребления товара ведет к росту предельной полезности в точке оптимума, значит, достижение заданного уровня полезности М потребует меньших затрат. Выражается этот эффект в снижении индекса цен потребителя. Можно проследить этот эффект, если принять цены на все промышленные товары равными:

(6.13)

Из уравнения для спроса (6.11) можно видеть, что снижение индекса цен действительно снижает спрос на каждую разновидность при прочих равных условиях. Как уже отмечалось выше, сила эффекта определяется кривизной кривых безразличия или эластичностью замещения σ. Чем ниже эластичность, тем больше разновидностей будет на рынке при прочих равных условиях, и тем сильнее будет снижаться индекс цен при увеличении числа разновидностей. Более того, сам индекс будет ниже при низкой эластичности (при прочих равных условиях). Можно сказать, что увеличение разновидностей промышленных товаров усиливает конкуренцию и снижает уровень цен.

Транспортные издержки

Пусть существует плоскость, на которой в R различных городах живут люди и производят промышленные товары, причем у этих разновидностей товаров одинаковая технология и цена. Так, в городе r производится n разновидностей по цене FOB (free on board) или цена у ворот завода с погрузкой на транспорт покупателя каждая. Сельскохозяйственные и промышленные товары перевозятся между городами с издержками, так что из каждой единицы отправленного из города r в город s товара только доезжает, остальное исчезает по дороге. Таким образом, чтобы получить единицу товара в городе s, надо из города r отправить единиц товара.

Соответственно цена единицы товара, привезенного в город S из r, будет равна

Тогда индекс цен в городе S будет равен

(6.14)

Если в (6.11) также подставить конечную цену товара, привезенного из города r, то мы получим спрос на данный товар в городе s. Однако чтобы туда доставить единицу товара, потребуется в городе r произвести единиц этого товара. Тогда суммарный спрос по всем городам s на разновидность товара, произведенную в городе r, будет равен

(6.15)