Модель Брауна (модель экспоненциального сглаживания)

Модель Брауна может отображать развитие не только в виде линейной тенденции, но также в виде случайного процесса, не имеющего тенденции, а также в виде изменяющейся параболической тенденции. Соответственно различают модели Брауна:

* нулевого порядка, которая описывает процессы, не имеющие тенденции развития. Она имеет лишь один параметр а0 (оценка текущего уровня). Прогноз развития на τ шагов вперед осуществляется согласно формуле . Такая модель еще называется "наивной" ("будет, как было"). Доверительный интервал прогноза получают по формуле^[1] ;

• первого порядка .Коэффициент значение, близкое к последнему уровню, и представляет как бы закономерную составляющую этого уровня. Коэффициентопределяет прирост, сформировавшийся в основном к концу периода наблюдений, но отражающий также (правда, в меньшей степени) скорость роста на более ранних этапах. Прогноз осуществляется по формуле . Доверительный интервал прогноза получают по формуле

• второго порядка, отражающую развитие в виде параболической тенденции с изменяющимися "скоростью" и "ускорением". Она имеет три параметра (– оценка текущего прироста или "ускорение"). Прогноз осуществляется по формуле

Рассмотрим этапы построения линейной адаптивной модели Брауна.

Этап 1. По первым пяти точкам временного ряда оцениваются значения и параметров модели с помощью метода наименьших квадратов для линейной аппроксимации по формуле

Этап 2. С использованием параметров и , которые соответствуют нулевому моменту времени, по модели Брауна находим прогноз на первый шаг (τ =1):

Этап 3. Расчетное значение экономического показателя сравнивают с фактическим значением и находят величину отклонения :

Для всех остальных членов ряда отклонение (остаточная компонента) находится по формуле , которое используют для корректировки параметров модели в соответствии с принятой схемой.

Этап 4. Корректируют параметры модели и по следующим формулам:

(5.23)

где β – коэффициент дисконтирования данных, отражающий большую степень доверия более поздним наблюдениям; а – параметр сглаживания (). Оптимальное значение β находится итеративным путем, т.е. многократным построением модели при разных значениях β и выбором наилучшей. Параметры вычисляются последовательно, от уровня к уровню, и их значения для последнего уровня определяют окончательный внд модели.

Этап 5. По модели со скорректированными параметраминаходят прогноз на следующий момент времени ():

Этап 6. Возврат на пункт 3, если t = n.

Если t = п, то построенную модель можно использовать для прогнозирования на будущее. Точечный прогноз рассчитывается по формуле

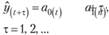
Пример 5.3. Построим прогноз по линейной модели Брауна.

По имеющейся информации (у в табл. 5.6) об объемах продаж нового товара (тыс. руб.) в течение 35 недель построить адаптивную модель Брауна с линейной тенденцией. Построить прогноз на три шага вперед, используя значение параметра сглаживания 0,3. Результаты моделирования и прогнозирования привести на графике.

Таблица 5.6

t	1	2	3	4	5	6	7
y	27,30	41,80	42,80	56,20	72,50	56,00	79,00

t	8	9	10	11	12	13	14
y	74,90	103,30	111,30	125,20	189,30	169,10	193,50

t	15	16	17	18	19	20	21
t	207,40	221,20	267,20	264,00	273,80	321,00	317,40

t	22	23	24	25	26	27	28
t	342,00	350,60	368,50	397,00	382,90	400,60	409,40

t	29	30	31	32	33	34	35
y	426,00	402,00	398,70	418,10	424,60	435,10	439,8

1) По первым пяти точкам временного ряда оцениваются значения и параметров модели с помощью метода наименьших квадратов для линейной аппроксимации:

Получаем начальные значения параметров модели и , которые соответствуют моменту времени t = 0.

2) С использованием параметров и по модели Брауна находим прогноз на первый шаг () :

3) Находим величину отклонения:

Все расчеты в табл. 5.7 показаны для

4) Корректируем параметры моделиипо следующим формулам:

Таблица 5.7

Оценка параметров модели Брауна

t	y_t	a₀	a₁
0		16,68	10,48
1	27,3	27,231	10,493	27,160	0,140	0,513
2	41.8	39,803	10,859	37,724	4,076	9,751
3	42,8	46,652	10,152	50.662	-7,862	18,370
4	56,2	56,496	10,097	56,804	-0,604	1,075
5	72,5	69,606	10,629	66,594	5,906	8,147
...	...	...	...	...	...	...
32	418,1	419,625	6,628	421,213	-3,113	0,744
33	424,6	425,410	6,479	426,254	-1,654	0,389
34	435,1	433,527	6,768	431,890	3,210	0,738
35	439,8	440,043	6,724	440,295	-0,495	0,113

5) По модели со скорректированными параметрами находим прогноз на следующий момент времени

Возврат к пункту 3.

Вычисления повторяем до конца наблюдений.

6) Параметры модели, полученные в последний момент времени (t = 35), используем для построения прогноза на три недели вперед ();

Результаты прогнозирования по модели Брауна представлены графически на рис. 5.1.

Рис. 5.1. Исходные данные, результаты моделирования (альфа = 0,3) и точечный прогноз

В моделях Брауна и Хольта параметры сглаживания характеризуют степень адаптации модели к изменению ряда наблюдений. Они определяют скорость реакции модели на изменения, происходящие в развитии. Чем они больше, тем быстрее реагирует модель на изменения. Обычно для устойчивых рядов их величина большая, а для неустойчивых – маленькая. В различных методах прогнозирования используется различный подход к их определению. Их можно взять фиксированными, а наилучшее значение определить методом подбора, чтобы ошибка прогноза на один шаг вперед была наименьшей. При использовании компьютера это не представляет труда. Альтернативу этому подходу составляет динамическое изменение параметров сглаживания. В методах эволюции и симплекс-планирования параметры адаптации постоянно меняются на каждом шаге. Для каждого параметра сглаживания формируется несколько значений.