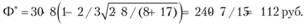Модели управления запасами
Под задачей управления товарными запасами понимается такая оптимизационная задача, в которой задана информация:
– о поставках товара;
– о спросе на товар;
– об издержках и условиях хранения товарных запасов;
– критерий оптимизации.
Рассмотрим задачу управления запасами в так называемой классической постановке. Выберем за единичный интервал времени один день. Пусть к концу дня t – 1 на складе находится запас товара в объеме 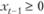 . Склад делает заказ на пополнение запаса товара в объеме
. Склад делает заказ на пополнение запаса товара в объеме 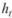 . Это пополнение поступает к началу следующего дня ht,, так что запас товара в начале следующего дня составляет
. Это пополнение поступает к началу следующего дня ht,, так что запас товара в начале следующего дня составляет 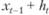 . Пусть
. Пусть 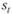 – объем товара, запрашиваемый потребителем (или потребителями) в день t (объем заявки).
– объем товара, запрашиваемый потребителем (или потребителями) в день t (объем заявки).
Если 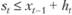 , то склад удовлетворяет заявку потребителя полностью, а остатки товара.
, то склад удовлетворяет заявку потребителя полностью, а остатки товара.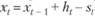 переносятся на следующий день t+1, причем издержки хранения этого запаса пропорциональны его объему и равны
переносятся на следующий день t+1, причем издержки хранения этого запаса пропорциональны его объему и равны
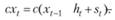
Если объем заявки st > xt-1 + ht, то склад полностью отдает свой запас, а за недопоставленный товар несет потери (например, штрафуется за дефицит), пропорциональные объему дефицита и равные
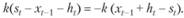
Таким образом, полные издержки 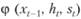 склада можно записать в виде:
склада можно записать в виде:
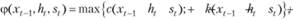 (8.-25)
(8.-25)
при этом остаток товара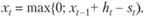
Из (8.25) следует:
если  ,то
,то 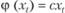 ;
;
если 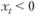 ,то
,то 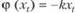 ;
;
если 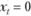 ,то
,то 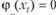 .
.
В классической постановке задачи управления запасами предполагается, что сама величина спроса st неизвестна, однако известно, что она является независимой случайной величиной, имеющей заданный закон распределения. Пусть распределение вероятностей величины 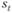 задается непрерывной функцией распределения F(x) с плотностью распределения f(x). Тогда средние полные издержки
задается непрерывной функцией распределения F(x) с плотностью распределения f(x). Тогда средние полные издержки 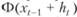 задаются формулой (М – математическое ожидание)
задаются формулой (М – математическое ожидание)
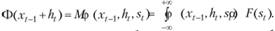
Задача ставится таким образом: определить объем заказа на пополнение ht, минимизирующий средние полные издержки, т.е.
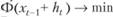 , где
, где 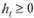
Рассмотрим решение классической задачи управления товарными запасами в статической постановке. Обозначим 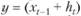 и опустим ввиду статичности задачи индекс t в записи объема спроса и пополнения. Рассмотрим следующую задачу:
и опустим ввиду статичности задачи индекс t в записи объема спроса и пополнения. Рассмотрим следующую задачу:
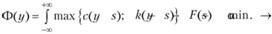 (8.26)
(8.26)
Перепишем функцию Ф(//) в более удобном виде:
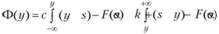 (8.26')
(8.26')
и вычислим ее первую производную:
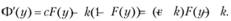
Заметим, что вторая производная этой функции неотрицательна (т.е. функция выпукла вниз):
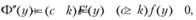
поэтому, приравняв первую производную нулю, получим уравнение для минимизирующего запаса 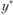 :
:
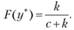 (8.27)
(8.27)
Решение (8.27) задачи (8.26) определяет стратегию оптимального пополнения запасов. Величина пополнения запасов 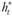 , минимизирующая средние полные издержки, задается следующим правилом:
, минимизирующая средние полные издержки, задается следующим правилом:
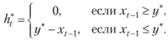 (8.28)
(8.28)
Конкретные числовые характеристики системы управления запасами зависят от вида функции плотности распределения f(x) случайной величины спроса. В качестве примера рассмотрим случай симметричного "треугольного" распределения спроса, при котором функция плотности распределения имеет график, представленный на рис. 8.10, а. Очевидно, этот график получается параллельным переносом вправо (заменой х на х – а) графика, изображенного на рис. 8.10, б, функции
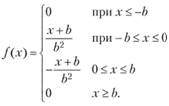 (8.29)
(8.29)
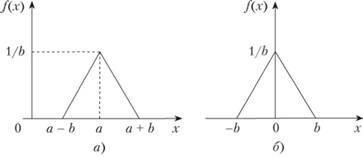
Рис.. 8.10
Вычислим числовые характеристики для функции плотности распределения, заданной в (8.29) (рис 8.10, б). В этом случае функция распределения F(x) задается формулой
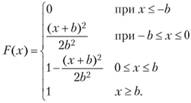 (8.30)
(8.30)
Случайная величина спроса s имеет следующие числовые характеристики: математическое ожидание Ms = 0; математическое ожидание квадрата 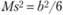 ; дисперсия
; дисперсия 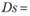
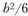 , среднее квадратическое отклонение
, среднее квадратическое отклонение 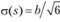
Непосредственные вычисления с использованием функции средних полных издержек в виде (8.26') показывают, что при
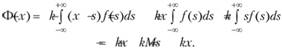 (8.31)
(8.31)
Используя выражение для первой производной 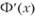 и выражение (8.30) для функции распределения
и выражение (8.30) для функции распределения  можно определить, что при
можно определить, что при 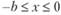
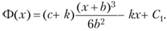 (8.32)
(8.32)
Здесь константа интегрирования С1 определяется путем приравнивания выражения (8.31) и (8.32) при 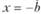 :
:
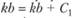 , т.е.
, т.е. 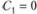
Аналогично при 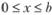 можно получить:
можно получить:
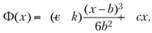 (8.33)
(8.33)
а при 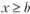 :
:
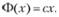 (8.34)
(8.34)
Выражения (8.31)-(8.34) задают в разных интервалах искомую функцию средних полных издержек. Заменяя в ней x на х – а, получим функцию средних полных издержек, если функция плотности распределения спроса имеет вид, изображенный на рис. 8.10, а. Для иллюстрации график функции средних полных издержек для такой функции спроса в случае k > с представлен на рис. 8.11, где оптимальный уровень запаса 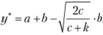
В общем виде для данной функции плотности распределения спроса оптимальный уровень запаса задается формулами
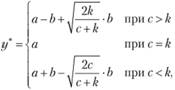 (8.35)
(8.35)
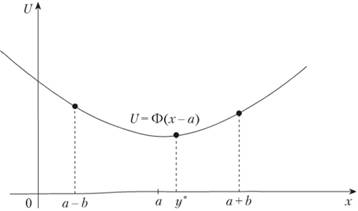
Рис. 8.11
а значение 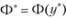 минимума средних полных издержек имеет вид
минимума средних полных издержек имеет вид
Из формул (8.35) и (8.36) для данной модели следует, что оптимальный уровень запаса при  и минимум средних полных издержек при всех с, k линейно зависят от величины b, т.е. от длины интервала разброса значений величины спроса на товар.
и минимум средних полных издержек при всех с, k линейно зависят от величины b, т.е. от длины интервала разброса значений величины спроса на товар.
Напомним, что стратегия оптимального пополнения запасов задается формулами (8.28).
Пример 8.3. Пусть некоторая фирма в соответствии с договором реализует со склада по заявкам холодильники, причем ежедневный спрос является случайной величиной, функция плотности распределения которой представлена графически на рис. 8.10, а и колеблется от 20 до 80 холодильников в день. Средние издержки хранения одного холодильника в день составляют 8 руб., а штраф за дефицит (недопоставку) одного холодильника в день равен 17 руб. Требуется определить стратегию
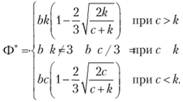 (8.36)
(8.36)
оптимального пополнения запаса холодильников и минимальные средние полные издержки.
В условиях рассматриваемой задачи b = (80 – 20)/2 = 30 (хол.); а = (20 + 80/2 = 50 (хол.); с = 8 руб.; k = 17 руб.
В соответствии с формулой (8.35) оптимальный уровень запаса (с < k) составляет

Тогда величина 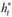 пополнения запаса холодильников фирмой, при которой средние полные издержки будут минимальны, задается в соответствии с формулой (8.28) правилом:
пополнения запаса холодильников фирмой, при которой средние полные издержки будут минимальны, задается в соответствии с формулой (8.28) правилом:
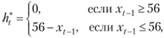
где 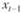 – запас холодильников на складе фирмы на конец предыдущего дня. Так, если на конец предыдущего дня на складе фирмы было 60 холодильников, то пополнять запас не следует, а если на конец предыдущего дня на складе фирмы оставалось 25 холодильников, то следует реализовать заказ на пополнение запаса в количестве 56 – 25 = 31 холодильника.
– запас холодильников на складе фирмы на конец предыдущего дня. Так, если на конец предыдущего дня на складе фирмы было 60 холодильников, то пополнять запас не следует, а если на конец предыдущего дня на складе фирмы оставалось 25 холодильников, то следует реализовать заказ на пополнение запаса в количестве 56 – 25 = 31 холодильника.
Если придерживаться этой стратегии пополнения запаса холодильников, то минимальный уровень средних полных издержек в расчете на один день в соответствии с формулой (8.36) составит