Модели сетевого планирования и управления

Во многих областях экономики, технологии, проектирования, строительства, научных исследований важное значение имеют задачи оптимизации распределения ресурсов (трудовых, финансовых и др.). Особую значимость приобретают эти задачи в условиях реализации новых проектов, когда выполняется огромное количество взаимозаменяемых операций, в работу вовлекается множество работников, предприятий, организаций, так как в этих случаях управление работами усложняется новизной разработки, трудностью точного определения сроков и затрат ресурсов на том или ином этапе. Высокоэффективными инструментами для решения таких задач являются сетевые методы и модели.

Основные понятия сетевого моделирования

Сетевой моделью (другие названия: сетевой график, сеть) называется экономико-математическая модель, отражающая комплекс работ (операций) и событий, связанных с реализацией некоторого проекта (научно-исследовательского, производственного и др.), в их логической и технологической последовательности и связи. Анализ сетевой модели, представленной в графической или табличной (матричной) форме, позволяет, во-первых, более четко выявить взаимосвязи этапов реализации проекта и, во-вторых, определить наиболее оптимальный порядок выполнения этих этапов в целях, например, сокращения сроков выполнения всего комплекса работ. Таким образом, методы сетевого моделирования можно отнести к методам принятия оптимальных решений.

Математический аппарат сетевых моделей базируется на теории графов. Графом называется совокупность двух конечных множеств: множества точек, которые называются вершинами, и множества пар вершин, которые называются ребрами. Представление о графе можно получить, если рассмотреть некоторый геометрический многогранник, например куб; в кубе можно выделить два конечных множества, состоящих соответственно из восьми вершин и двенадцати ребер.

Если рассматриваемые пары вершин являются упорядоченными, т.е. на каждом ребре задается направление, то граф называется ориентированным; в противном случае – неориентированным. Последовательность неповторяющихся ребер, ведущая от некоторой вершины к другой, образует путь. Граф называется связным, если для любых двух его вершин существует путь, их соединяющий; в противном случае граф называется несвязным. В экономике чаще всего используется два вида графов: дерево и сеть. Дерево представляет собой связный граф без циклов, имеющий исходную вершину (корень) и крайние вершины; пути от исходной вершины к крайним вершинам называются ветвями. Сеть – это ориентированный конечный связный граф, имеющий начальную вершину (источник) и конечную вершину (сток). Таким образом, сетевая модель представляет собой граф вида "сеть".

В экономических исследованиях сетевые модели возникают при моделировании экономических систем и процессов методами сетевого планирования и управления (СПУ).

Объектом управления в системах сетевого планирования и управления являются коллективы исполнителей, располагающие определенными ресурсами и выполняющие заданный комплекс операций, который призван обеспечить достижение намеченной цели, например разработку нового изделия, строительство объекта и т.п.

Основой СПУ служит сетевая модель (СМ), в которой моделируется совокупность взаимосвязанных работ и событий, отображающих процесс достижения определенной цели. Она может быть представлена в виде графика или таблицы.

Основными понятиями СМ являются следующие: работа, событие, путь. На рис. 3.7 графически представлена СМ, состоящая из 5 событий (кружочки) и 6 работ (стрелки); продолжительность выполнения работ в некоторых единицах времени указана над стрелками.

Работа характеризует материальное действие, требующее использования ресурсов, или логическое, требующее лишь взаимосвязи событий. При графическом распределении работа изображается стрелкой, которая соединяет два

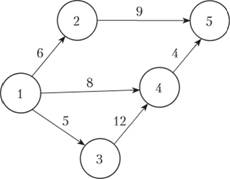
Рис. 3.7. Сетевая модель

события. Она обозначается парой заключенных в скобки чисел (i, j), где i – номер события, из которого работа выходит, a j – номер события, в которое она входит. Работа не может начаться раньше, чем свершится событие, из которого она выходит. Каждая работа имеет определенную продолжительность. Например, запись 1(2, 5) = 9 означает, что работа (2, 5) имеет продолжительность 9 единиц времени (см. рис. 3.7). К работам относятся также такие процессы, которые не требуют ни ресурсов, ни времени выполнения. Они заключаются в установлении логической взаимосвязи работ и показывают, что одна из них непосредственно зависит от другой и не может выполняться, прежде чем эта другая будет завершена; такие работы называются фиктивными и на графике изображаются пунктирными стрелками.

Событиями называются результаты выполнения одной или нескольких работ. Они не имеют протяженности во времени. Событие свершается в тот момент, когда оканчивается последняя из работ, входящая в него. События обозначаются одним числом и при графическом представлении СМ изображаются кружком (или иной геометрической фигурой), внутри которого проставляется его порядковый номер (i = 1, 2, ... N). В СМ имеется начальное событие (с номером 1), из которого работы только выходят, и конечное событие (с номером N), в которое работы только входят.

Путь в СМ – это цепочка следующих друг за другом работ, соединяющих начальную и конечную вершины, например, в приведенной на рис. 3.7 модели путями являются L1 = (1, 2, 5), L2 = (1, 4, 5) и др. Продолжительность пути определяется суммой продолжительностей составляющих его работ. Путь, имеющий максимальную длину, называют критическим и обозначают Lкр, а его продолжительность – tкр. Работы, принадлежащие критическому пути, называются критическими. Их несвоевременное выполнение ведет к срыву сроков всего комплекса работ.