Модели равновесного ценообразования
В настоящий момент существует две основные модели равновесного ценообразования – САРМ и АРТ. Каждая из них описывает доходность актива при рыночном равновесии, однако они предполагают разные способы прихода рынка к равновесию. Отметим, что обе модели довольно старые – 1964 и 1976 г. соответственно, хотя до сих пор активно используются в практике.
Модель оценки долгосрочных активов
Данную модель практически в одно и то же время разработали У. Шарп, Я. Моссин и Д. Линтнер. Здесь мы изложим описание модели САРМ (capital asset pricing model) в современной трактовке, с авторскими выводами модели можно ознакомиться, прочитав первоисточники.
Авторы модели исходили из того, что если рынок находится в равновесии, то любой актив должен обеспечивать одно и то же вознаграждение за единицу своего риска. Кроме того, данное вознаграждение должно относиться только к риску актива, который нельзя убрать с помощью диверсификации. Таким образом, риск отдельного актива всегда можно представить в виде двух слагаемых – риск систематический и риск уникальный.
Диверсификация портфеля
Диверсификация риска портфеля заключается в том, что при увеличении числа активов в портфеле его риск снижается. Риск портфеля, как и риск отдельного актива, состоит из двух основных частей – систематического (рыночного) и уникального риска.
Так, на рис. 5.12 общий риск некоторого портфеля равен длине отрезка ,4 С. Этот риск состоит из двух частей: длина отрезка АН описывает уникальный риск, а длина отрезка ВС описывает рыночный риск. Видно, что при движении вправо, т.е. увеличении числа активов в портфеле, длина отрезков, аналогичных отрезку АВ уменьшается. При неограниченном числе активов в составе портфеля его риск сведется к величине, равной длине отрезка ВС. Эта величина – средняя ковариация между доходностями всех активов, существующих на рынке.
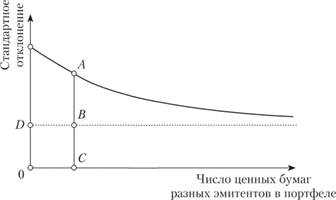
Рис. 5.12. Диверсификация портфеля
В диверсифицированном портфеле уникальные риски активов отсутствует. Самый диверсифицированный из всех возможных портфелей – рыночный портфель, в который входят все торгуемые и неторгуемые активы с весами, пропорциональными их капитализации по отношению к капитализации рынка в целом. Поскольку рыночный портфель максимально диверсифицирован, то он содержит исключительно систематический риск, который нельзя устранить диверсификацией. Следовательно, рынок вознаграждает только за систематический риск, который берет на себя инвестор. Если инвестор по тем или иным причинам не стремится вместо одного актива купить много разных (создав диверсифицированный портфель), то рынок за взятый на себя инвестором уникальный риск вознаграждать не будет.
Как же определить, какую часть общего риска актива, измеряемого дисперсией или стандартным отклонением, занимает систематический риск? Допустим, что старый рыночный портфель состоял из п активов и имел риск, равный 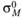 . Теперь предположим, что появился еще один актив и новый рыночный портфель состоит из п + 1 актива, а его риск равен
. Теперь предположим, что появился еще один актив и новый рыночный портфель состоит из п + 1 актива, а его риск равен  Очевидно, что добавление еще одного актива в диверсифицированный портфель может вызвать увеличение его систематического риска только за счет собственного систематического риска. Другими словами,
Очевидно, что добавление еще одного актива в диверсифицированный портфель может вызвать увеличение его систематического риска только за счет собственного систематического риска. Другими словами, 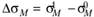 , это и есть систематический риск п + 1 актива. Данный прирост риска рыночного портфеля можно измерить с помощью производной, которая показывает, насколько изменится функция, если аргумент вырастет на единицу.
, это и есть систематический риск п + 1 актива. Данный прирост риска рыночного портфеля можно измерить с помощью производной, которая показывает, насколько изменится функция, если аргумент вырастет на единицу.
Запишем риск рыночного портфеля:
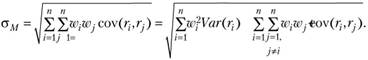
Тогда первая производная 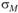 по
по 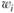 (так как добавление i-го актива в портфель эквивалентно увеличению веса данного актива с нуля до
(так как добавление i-го актива в портфель эквивалентно увеличению веса данного актива с нуля до 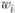 ) будет равна
) будет равна

Тогда, используя формулу (5.16), получаем, что ожидаемая доходность i-го актива должна удовлетворять следующему уравнению:
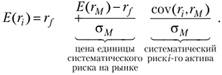 (5.17)
(5.17)
Таким образом, уравнение (5.17) может быть проинтерпретировано так: доходность г-ro актива в состоянии равновесия должна складываться из двух компонент – платы за отложенное потребление (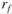 ) и рыночного вознаграждения за взятый на себя систематический риск i-го актива. Однако уравнение (5.17) чаще записывают в форме
) и рыночного вознаграждения за взятый на себя систематический риск i-го актива. Однако уравнение (5.17) чаще записывают в форме
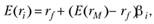 (5.17а)
(5.17а)
где 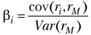 – коэффициент "бета" i-го актива.
– коэффициент "бета" i-го актива.
Уравнение (5.17а) задает линию, которую называют линией рынка ценных бумаг (security market line, SML), так как она описывает связь между доходностью и систематическим риском /-го актива в состоянии рыночного равновесия.
Если линия CML важна для определения состава рыночного портфеля и оптимального портфеля для инвестора, то линия SML важна для поиска неверно оцененных активов.
Как уже говорилось, активы, оцененные верно, должны лежать на линии SML. Активы, которые оценены неверно, будут лежать либо выше, либо ниже линии SML (рис. 5.13).
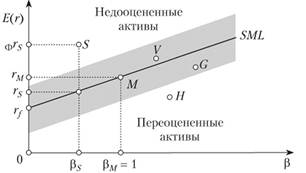
Рис. 5.13. Использование линии рынка ценных бумаг
Можно математически доказать, что любой актив, входящий в рыночный портфель с ненулевым весом, будет лежать на прямой SML, если рынок находится в состоянии равновесия. Однако не все активы могут быть оценены верно в конкретный момент времени, поэтому активы могут находиться выше или ниже линии SML. Так, актив S (см. рис. 5.13) должен иметь доходность rs, но фактически имеет доходность 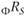 . Так как
. Так как  то цена актива S сейчас ниже, чем должна быть в состоянии равновесия, т.е. этот актив сейчас недооценен. Разница между фактической доходностью актива и доходностью актива в состоянии равновесия называется коэффициентом "альфа" актива
то цена актива S сейчас ниже, чем должна быть в состоянии равновесия, т.е. этот актив сейчас недооценен. Разница между фактической доходностью актива и доходностью актива в состоянии равновесия называется коэффициентом "альфа" актива 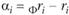 , и используется для управления портфелем (на ее основе выясняют, какой актив следует исключить из портфеля, какой включить).
, и используется для управления портфелем (на ее основе выясняют, какой актив следует исключить из портфеля, какой включить).
Таким образом, все активы, лежащие выше линии SML (с положительной "альфой"), представляют собой недооцененные активы, цена которых в ближайшее время будет повышаться. Активы, которые лежат ниже линии SML (с отрицательной "альфой"), являются переоцененными, и их цена будет снижаться.
Пример 5.5. На фондовом рынке представлены только три равные по капитализации компании А, В и С. Годовые доходности обыкновенных акций компаний А, В и С равны 15, 5,5 и 9% соответственно. Про компании А и В известно, что 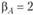 , а
, а 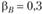 . Дополнительно известно, что акции компании А оценены верно, а у компании В
. Дополнительно известно, что акции компании А оценены верно, а у компании В 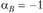 п.п. Определите, переоценены, недооценены или оценены верно акции компании С (ответ следует обосновать расчетами).
п.п. Определите, переоценены, недооценены или оценены верно акции компании С (ответ следует обосновать расчетами).
Решение
По компаниям А и В, составляя систему уравнений модели САРМ, находим параметры рынка (безрисковую доходность (x) и рыночную премию за риск (у)):
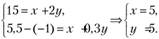
Поскольку все три компании образуют рынок, то можно найти коэффициент "бета" третьей компании, помня, что рыночный коэффициент "бета" всегда равен единице:
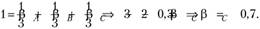
Теперь можно найти, какую доходность должны демонстрировать акции компании С:
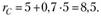
Следовательно, акции компании С являются недооцененными, так как их доходность больше доходности по модели САРМ.
Таким образом, если актив не лежит на линии SML, то его цена в ближайшее время будет меняться, и в зависимости от этого его следует покупать или продавать. Если актив лежит на линии SML, то считается, что его цена находится в равновесии и меняться не будет.
Однако из-за наличия налогов и комиссионных брокеру при совершении сделок не со всеми активами имеет смысл проводить сделки. Так, на рис. 5.13 с активами G и V не следует осуществлять сделок, так как их цена отличается от равновесной цены на величину меньшую, чем будет уплачено комиссий и налогов. Закрашенная область показывает зону, в которой не стоит с активами проводить сделки, даже если их цена отличается от равновесной.
Пример 5.6. Пусть уравнение линии SML задано формулой 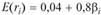 Аналитик подсчитал, что коэффициент "бета" для компании X равен 0,5, а для компании Y равен двум. Каковы должны быть доходности этих активов, чтобы их приобретение можно было считать хорошим вложением средств?
Аналитик подсчитал, что коэффициент "бета" для компании X равен 0,5, а для компании Y равен двум. Каковы должны быть доходности этих активов, чтобы их приобретение можно было считать хорошим вложением средств?
Решение
Для того чтобы инвесторы захотели купить эти активы, они должны быть недооценены. Поэтому вычисляем нижние границы доходностей, при которых активы будут недооценены:
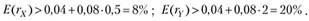
Следовательно, доходность акций компании X должна быть больше 8%, а компании Y – больше 20%.