Модели расчета показателей надежности восстанавливаемых и невосстанавливаемых систем различных типов

Большинство технических устройств являются сложными системами, состоящими из отдельных узлов, деталей, агрегатов, систем управления и т.п. Под сложной системой понимается объект, предназначенный для выполнения заданных функций, который может быть расчленен на элементы (компоненты), каждый из которых также выполняет определенные функции и находится во взаимодействии с другими элементами системы.

С позиций надежности сложная система обладает как отрицательными, так и положительными свойствами.

Факторы, отрицательно влияющие на надежность сложных систем, следующие:

• имеется большое число элементов, отказ каждого из которых может привести к отказу всей системы;

• оценить работоспособность сложных систем весьма затруднительно с точки зрения статистических данных, так как они часто являются уникальными или имеются в небольших количествах;

• даже у систем одинакового предназначения каждый экземпляр имеет свои незначительные вариации свойств отдельных элементов, что сказывается на выходных параметрах системы;

• чем сложнее система, тем большими индивидуальными особенностями она обладает.

Однако сложные системы обладают и рядом свойств, которые положительно влияют на их надежность:

• сложным системам свойственна самоорганизация, саморегулирование или самоприспособление, когда система самостоятельно способна найти наиболее устойчивое для своего функционирования состояние;

• для сложной системы часто возможно восстановление работоспособности по частям, без прекращения ее функционирования.

Кроме того, не псе элементы системы одинаково влияют на надежность сложной системы.

Анализ работоспособности сложной системы связан с изучением ее структуры и тех взаимосвязей, которые определяют ее надежное функционирование.

При анализе надежности сложных систем их разбивают на элементы (компоненты) с тем, чтобы вначале рассмотреть параметры и характеристики элементов, затем оценить работоспособность всей системы. Под элементом, точнее говоря, элементом расчета надежности можно понимать составную часть сложной системы, которая может характеризоваться самостоятельными входными и выходными параметрами. При исследовании надежности системы элемент не расчленяется на составные части, и показатели безотказности и долговечности относятся к элементу в целом. При этом возможно восстановление работоспособности элемента независимо от других частей и элементов системы.

Анализ надежности сложных систем имеет специфические особенности. Различные отказы, а также снижение работоспособности элементов системы по-разному оказывают влияние на надежность всей системы.

При анализе надежности сложной системы все ее элементы и компоненты целесообразно разделить на следующие группы:

• элементы, отказ которых практически не влияет на работоспособность системы (деформация ограждающего кожуха машины, изменение окраски поверхности и т.п.). Отказы (т.е. неисправное состояние) этих элементов могут рассматриваться изолированно от системы;

• элементы, работоспособность которых за рассматриваемый период времени практически не изменяется (станины и корпусные детали, малонагруженные элементы с большим запасом прочности);

• элементы, ремонт или регулировка которых возможны при работе изделия или во время остановок, не влияющих на его эффективность (подналадка и замена режущего инструмента на станке, регулировка холостого хода карбюратора автомобильного двигателя);

• элементы, отказ которых приводит к отказам системы.

Таким образом, рассмотрению и анализу, с точки зрения надежности, подлежат лишь элементы последней группы. Как правило, имеется ограниченное число элементов, которые в основном и определяют надежность изделия. Эти элементы и подсистемы выявляются при рассмотрении структурной схемы параметрической надежности.

Рассмотрим понятия структурной надежности изделий и резервирования.

Структурной надежностью системы (устройства) называется результирующая надежность системы (устройства) при заданной ее структуре и известных значениях надежности всех входящих в нее частей (блоков, ячеек, компонентов и т.д., т.е. конструктивов).

Вообще с позиций теории систем правильнее говорить о над- системе, системе, подсистеме как составляющих некоторой сверхсистемы.

Модели надежности устанавливают связь между подсистемами (или элементами системы) и их влиянием на работу всей системы.

Структурная (эквивалентная) схема надежности (С(Э)СН или просто ССН) – это модель реального объекта, строящаяся на основе или с учетом, например, электрической схемы, топологии, типа паяных соединений, способа резервирования. Иначе говоря, ССН изделий – это обобщенная модель частных моделей (подмоделей) и значимых для надежности реальных частей изделия. Структурная схема надежности определяет функциональную взаимосвязь между работой подсистем (или элементов) в определенной последовательности. Эту схему составляют по принципу функционального назначения соответствующих подсистем (или элементов) при выполнении ими определенной части работы, выполняемой системой в целом.

Техническая система может быть сконструирована таким образом, что для успешного се функционирования необходима исправная работа всех ее элементов. В этом случае ее называют последовательной системой (S-тип). Есть также системы, в которых при отказе одного элемента другой элемент способен выполнить его функции. Такую систему называют параллельной (Р-тип). Очень часто системы обладают свойствами как параллельных, так и последовательных систем – системы со смешанным соединением (С-тип). При расчете надежности необходимо исследовать действия системы, основываясь на ее функциональной структуре и используя вероятностные соотношения.

Такое исследование структуры позволяет выявить узкие места в конструкции системы с точки зрения ее надежности, а на этапе проектирования – разработать конструктивные меры по устранению подобных узких мест. Например, можно заранее подсчитать, сколько резервных элементов необходимо для обеспечения заданного уровня надежности системы. Далее можно рассчитать надежность системы, построенной из элементов с известной надежностью, или наоборот, исходя из требования к надежности системы, предъявить требования к надежности элементов.

Поскольку резервирование – весьма эффективный метод повышения надежности изделий, то целесообразно дать определения некоторых основных терминов из теории резервирования (табл. 5.18), а затем рассмотреть отдельные типовые ССН (рис. 5.1) и ключевые показатели надежности (вначале без использования резервирования, а затем и с его применением).

Таблица 5.18

Основные термины теории резервирования

Термин	Определение
Резервирование (redundancy)	Способ обеспечения надежности объекта за счет использования дополнительных средств и (или) возможностей, избыточных но отношению к минимально необходимым для выполнения требуемых функций
Резерв	Совокупность дополнительных средств и (или) возможностей, используемых для резервирования
Основной конструктив	Часть объекта, необходимая для выполнения требуемых функций без использования резерва
Резервируемый конструктив	Основной конструктив, на случай отказа которого в объекте предусмотрены один или несколько резервных конструктивов
Резервный конструктив	Конструктив, предназначенный для выполнения функции основного конструктива в случае отказа последнего
Нагруженный (горячий) резерв	Резерв, который содержит один или несколько резервных конструктивов, находящихся в режиме основного конструктива
Облегченный резерв	Резерв, который содержит один или несколько резервных конструктивов, находящихся в менее нагруженном режиме, чем основной конструктив
Ненагруженный (холодный) резерв	Резерв, который содержит один или несколько резервных конструктивов, находящихся в ненагруженном режиме до начала выполнения ими функции основного конструктива
Постоянное (комбинаторное резервирование)	Резервирование, при котором используется нагруженный резерв, и при отказе любого конструктива в резервированной группе выполнение объектом требуемых функций обеспечивается оставшимися конструктивами без переключений
Резервирование замещением (холодное ненагруженное резервирование)	Резервирование, при котором функции основного конструктива передаются резервному только после отказа основного конструктива
Смешанное резервирование	Сочетание различных видов резервирования в одном объекте

Примечание. Под термином "конструктив" следует понимать любую конструктивно законченную часть изделия.

Рис. 5.1. Типы ССН (никуда нс приходящие стрелки в ветвящейся структуре ССН в реальности могут быть резервными "проводами", служащими для быстрого подключения ЭРН 3-уровня)

Самой используемой (базовой) ССН без применения резервирования является ССН последовательного типа, или 5-типа (5 – serial). В структурных схемах надежности систем с последовательным соединением элементов (рис. 5.2) отказ одного элемента вызывает отказ другого элемента, а затем третьего и т.д. Например, большинство приводов машин и механизмов передач подчиняются этому условию. Так, если в приводе машины выйдет из строя любая шестерня, подшипник, муфта, рычаг управления, электродвигатель, насос смазки, то весь привод перестанет функционировать. При этом отдельные элементы в этом приводе не обязательно должны быть соединены последовательно. Такую структурную схему называют схемой с последовательным соединением зависимых элементов. В этом случае надежность системы определяют по теореме умножения для зависимых событий.

На рис. 5.2 представлена ССН изделия, состоящая из k частей, соединенных последовательно.

Рис. 5.2. ССН последовательного 5-типа без резервирования:

r1, ..., rk – ВБР каждого конструктива изделия

Если ВБР отдельных частей не зависят друг от друга, т.е. отказ любой части не меняет ВБР остальных частей изделия, то вероятность безотказной работы изделия Ps определяется произведением ВБР его частей:

Если однотипные (одинаковые) конструктивы системы соединены последовательно (5-тип), то ВБР изделия Rs составляет

где r – ВБР однотипных конструктивов; k – количество конструктивов в ССН.

Средняя наработка на отказ Ts для ССП этого типа выражается формулой

где λ – интенсивность отказов входящих в ССН одинаковых конструктивов.

На рис. 5.3 представлена ССН параллельного, или P-типа (Р – parallel) с применением горячего резерва, состоящая из k частей, соединенных параллельно в надежностном смысле.

Сложные системы, состоящие из элементов высокой надежности, могут обладать низкой надежностью за счет наличия большого числа элементов. Например, если узел состоит всего из 50 деталей, а вероятность безотказной работы каждой детали за выбранный промежуток времени составляет Ri = 0,99, то вероятность безотказной работы узла будет R(t) = 0,9950 = 0,605. Если же узел с аналогичной безотказностью элементов состоит из 400 деталей, то R(t) = 0,99400 = 0,018, т.е. узел становится практически неработоспособным.

Рис. 5.3. Фрагмент ССН Р-типа:

r1, ..., rk – ВБР каждого конструктива изделия

Пример 5.4

Определить надежность автомобиля (системы) при движении на заданное расстояние, если известны надежности следующих подсистем: системы зажигания r1 = 0,99; системы питания топливом и смазкой r2 = 0,999; системы охлаждения r3 = 0,998; двигателя r4 = 0,985; ходовой части r5 = 0,995.

Решение

Известно, что отказ любой подсистемы приводит к отказу автомобиля. Для определения надежности автомобиля используем вышеприведенную формулу:

Ответ: R = 0,967.

В практике проектирования сложных технических систем часто используют схемы с параллельным соединением элементов (см. рис. 5.3), которые построены таким образом, что отказ системы возможен лишь в случае, когда отказывают все ее элементы, т.е. система исправна, если исправен хотя бы один ее элемент. Такое соединение часто называют резервированием. В большинстве случаев резервирование оправдывает себя, несмотря на увеличение стоимости. Наиболее выгодным является резервирование отдельных элементов, которые непосредственно влияют на выполнение основной работы. При конструировании технических систем в зависимости от выполняемой системой задачи применяют горячее или холодное резервирование.

Горячее резервирование применяют тогда, когда не допускается перерыв в работе на переключение отказавшего элемента на резервный с целью выполнения задачи в установленное время. Чаще всего горячему резервированию подвергают отдельные элементы. Используют горячее резервирование элементов и подсистем, например источников питания (аккумуляторные батареи дублируются генератором и т.п.). Холодное резервирование используют в тех случаях, когда необходимо увеличение ресурса работы элемента, и поэтому предусматривают время на переключение отказавшего элемента на резервный.

Если конструктивы в ССН соединены параллельно (Р-тип), то ВБР изделия Rp выражается формулой

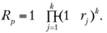
А если конструктивы однотипны, то формула для ВБР упрощается:

Структурная схема надежности P-типа отражает возможность отказа системы, если все ее конструктивы станут неработоспособными.

Существуют технические системы с частично параллельным резервированием, т.е. системы, которые оказываются работоспособными даже в случае отказа нескольких элементов (С-тип, С – combinatorial)).

На рис. 5.4 представлена ССН комбинаторного, или С-типа. Конструктивы в ССН соединены, как и в предыдущем случае, параллельно, но условием работоспособности системы является следующее требование: не менее h конструктивов должны быть работоспособными и только не более с (шт.) любых конструктивов из множества 1, ..., k могут отказать. Тогда ВБР изделия Rc имеет вид

где

– число сочетаний из к элементов по j.

Рис. 5.4. Фрагмент ССН комбинаторного тина (С-типа)

По этим формулам могут быть получены оценки показателей надежности мажоритарных схем резервирования (по большинству неотказавших конструктивов), а также изделий, в том числе ИМНЭ, использующих мажоритарную логику.

На рис. 5.5 представлена ССН изделия, разработанного с использованием ненагруженного (холодного) резерва, или Х-типа (х – холод). На рисунке в ССН используется ненагруженный (холодный) резерв. Причем если система содержит всего k конструктивов, из которых h = 1 – резервируемый конструктив, a (k – 1) – резервные, то при допущении простейшего потока отказов (см. далее свойства такого потока) ВБР изделия Rx в общем случае имеет вид

где t – время активной работы изделия; средняя наработка на отказ равна

Рис. 5.5. Фрагмент ССН с ненагруженным резервом – резервированием замещением (Х-типа)

Структурная схема надежности такого типа резервирования отражает возможность многократной замены, кратной (k – 1), отказавшего базового конструктива.

Следует отметить, что в практике проектирования технических систем часто используют структурные схемы надежности с параллельно-последовательным соединением элементов. Так, часто при проектировании систем с радиоэлектронными элементами применяют схемы, работающие по принципу два из трех, когда работоспособность обеспечивается благодаря исправному состоянию любых двух элементов.

Надежность такой схемы соединения определяют по формуле

где r(t) – надежность каждого элемента за время работы t (для всех элементов одинакова); q(t) = 1 r(t).

Широкое применение в проектировании нашли так называемые мостиковые схемы. Надежность такой схемы определяют из соотношения вида

Здесь все элементы также имеют одинаковую надежность. Различают структурные схемы надежности с поканальным и поэлементным резервированием.

Структурная схема надежности с поканальным резервированием показана на рис. 5.6, эта схема является комбинацией ССН S- и P-типов. Каждый канал является S-типом ССН.

Рис. 5.6. Структурная схема надежности с поканальным резервированием

Формула надежности выглядит следующим образом:

При

Если

В практике проектирования часто используют структурную схему надежности с поэлементным резервированием (рис. 5.7), которая представляет собой комбинацию ССН Р- и S-типов (наоборот, в отличие от структурной схемы на рис. 5.6).

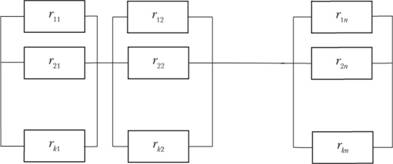
Рис. 5.7. Структурная схема надежности с поэлементным резервированием

Надежность такой системы определяют по формуле

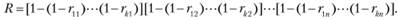
При

Если

Размышляем самостоятельно

Докажите, что структурная схема с поэлементным резервированием имеет более высокую надежность по сравнению с поканальным резервированием:

а) графоаналитическим способом по критерию надежности (ВБР);

б) минимаксным способом но критерию средней наработки (можно воспользоваться решением в книге [12]).

Пример 5.5

Техническая система предназначена для выполнения некоторой задачи. С целью обеспечения работоспособности система спроектирована со смешанным соединением элементов (рис. 5.8). Данная ССН является комбинацией S-, SP- и Р-типов.

Рис. 5.8. Структурная схема надежности технической системы

Определить надежность системы, если известно, что надежность се элементов равна:

Решение

При расчете надежности воспользуемся формулами как для последовательного, так и для параллельного соединения элементов:

Ответ: R = 0,56.

Очевидно, что полученный результат не очень хороший. Вероятность успешной работы системы с такой структурой составляет не многим более 50%. Поэтому необходимо, например, выбирать новую компонентную базу, перестраивать структуру системы, испытывать и т.д. Это позволит избежать соотношения (риска) 50 × 50: работает – не работает, опасно – безопасно и т.п.

Если, например, изменить величины ri: r1 = 0,99; r2 = 0,99; r3 = 0,9; r4 = 0,95; r5 = 0,9; r6 = 0,9; r7 = 0,8; r8 = 0,75; r9 = 0,7. Получим R = 0,927. Дополнительное задание. Проверьте правильность ответа.

Довольно полная систематизация разновидностей резервирования изделий, в том числе ИМНЭ, приведена на рис. 5.9. Систематизация разновидностей резервирования изделий основана на следующих положениях.

Рис. 5.9. Систематизация разновидностей резервирования изделий (ИМНЭ)

Различные резервированные с позиций надежности изделия отличаются друг от друга в первую очередь реакцией на появление отказа и могут быть разделены на изделия с активным и пассивным резервированием (см. [29, т. 10]).

При активном резервировании структура изделия такова, что при появлении отказа она перестраивается (при этом требуется время на перестройку), и изделие восстанавливает свою работоспособность. Частным случаем активного резервирования является резервирование замещением, при котором функции основного (резервируемого) конструктива передаются резервному только после отказа основного конструктива.

Для изделий с активным резервированием большое значение имеют условия работы резерва (степень нагруженности, или нагрузка) до появления отказа. Следует различать:

• нагруженный резерв, при котором резервные конструктивы и основной конструктив нагружены одинаково;

• облегченный резерв, при котором резервные конструктивы менее нагружены, чем основной конструктив;

• ненагруженный резерв, при котором резервные конструктивы практически не нагружены.

При пассивном резервировании изделий отказ одного или нескольких конструктивов не требует дополнительного времени на перестройку структуры изделия, поскольку все конструктивы соединены постоянно (изделие как бы мгновенно сопротивляется появлению отказов конструктивов). Если резервные конструктивы участвуют в функционировании изделия наравне с основными конструктивами, то такое резервирование называют постоянным.

При отказе хотя бы одного из конструктивов изделия с пассивным резервированием может изменяться нагрузка, воспринимаемая конструктивами, оставшимися работоспособными. По этому признаку различают три вида изделий с пассивным резервированием:

• с неизменной нагрузкой, в которых при отказе одного или нескольких конструктивов нс меняется нагрузка на конструктивы, оставшиеся работоспособными;

• с перераспределением нагрузки, в которых при отказе хотя бы одного конструктива изменяется (обычно увеличивается) нагрузка на конструктивы, оставшиеся работоспособными;

• с резервированием по нагрузке, в которых при отказе хотя бы одного конструктива интенсивность отказов оставшихся конструктивов снижается за счет того, что нагрузка, которую должен воспринимать один конструктив, воспринимается несколькими конструктивами.

При пассивном резервировании наибольший выигрыш в надежности достигается в изделиях с неизменной нагрузкой, наименьший – в изделиях с резервированием по нагрузке.

В изделиях с активным резервированием происходит нарушение работы на время с момента отказа основного конструктива до момента включения резервного. В изделиях, где такой перерыв недопустим принципиально, пассивное резервирование является единственно возможным.

Оба способа резервирования могут быть реализованы путем применения различных видов ССН (см. рис. 5.3–5.7). Принято различать резервирование: общее, раздельное, единичное, внутри- компонентное, скользящее, с избирательными схемами или мажоритарное и автономное (см. [29, т. 8]).

Общее резервирование состоит в резервировании изделий в целом. Благодаря своей простоте этот способ резервирования наиболее известен.

Раздельное резервирование заключается в резервировании изделий по отдельным частям.

Единичное резервирование состоит в дублировании конструктивов изделия, обычно с использованием пассивного резервирования. При единичном резервировании не нужно составление специальных ССН, а можно просто ставить на место каждого конструктива (согласно функциональной схеме изделия) его аналог – типовой резервный конструктив.

Внутрикомпонентное резервирование заключается в резервировании внутренних связей компонента, что сопряжено с изменением конструкции компонента. Это особенно важно знать для микро- и наноэлектронных устройств.

Скользящее резервирование применяется в ИМНЭ из одинаковых конструктивов (в резервировании по способу замещения основной конструктив один, а резервных – один и более). Оно состоит в том, что используется небольшое число резервных конструктивов, которые могут подключаться взамен любого из отказавших конструктивов ИМНЭ.

При мажоритарном резервировании сравниваются сигналы на выходе нечетного числа параллельно работающих устройств, и во внешнюю цепь выдается сигнал, имеющийся на выходе большинства устройств.

Автономное резервирование – один из вариантов общего, заключается в применении нескольких независимо работающих изделий, построенных по разному принципу и выполняющих одну и ту же задачу. Такое резервирование применяется в ИМНЭ ответственного назначения и всегда является пассивным.

Резервированные изделия можно различать по принципу их обслуживания: без профилактики, с периодической профилактикой и восстанавливаемые в процессе работы.

Показатели надежности ремонтируемых объектов, невосстанавливаемых в процессе применения, вычисляются по наработке. Суммарная наработка до возникновения и-го отказа равна

где – наработка между (i – 1 )-м и i-м отказами.

Возможны два пути оценки надежности ремонтируемых объектов:

• вычисление характеристик потока отказов;

• вычисление условных распределений наработки между отказами.

Первый путь в настоящее время является общепринятым. Рассматриваются потоки случайных событий, каждое из которых состоит в появлении отказа объекта. Поток отказов можно характеризовать ведущей функцией потока Ω(t) – математическим ожиданием числа отказов на интервале (0, t). Однако чаще в качестве показателя надежности используют параметр потока отказов – плотность вероятности возникновения отказа ремонтируемого объекта, определяемую для рассматриваемого момента суммарной наработки. Это определение нуждается в пояснении.

В теории массового обслуживания при изучении потоков событий применяют следующие две характеристики:

интенсивность потока событий

(5.4)

и параметр потока событии

(5.5)

где Pk(t, t + Δt) – вероятность появления k событий во временно́м интервале (t, t + Δt).

Потоки отказов являются ординарными потоками, т.е. вероятность совмещения в один и тот же момент двух и более отказов пренебрежимо мала. Иначе говоря,

Для ординарных потоков отказов выражения (5.4) и (5.5) упрощаются, интенсивность и параметр потока отказов совпадают:

где P1(t, t + Δt) – вероятность появления одного отказа во временно́м интервале (t + Δt); o(Δt) – бесконечно малая величина более высокого порядка малости, чем At. Она характеризует вероятность появления двух и более отказов в интервате (t, t + Δt).

Чтобы не смешивать с интенсивностью отказов перемонтируемых изделий, применяют термин "параметр потока отказов".

Обычно рассматривают две математические модели случайных потоков отказов.

Количественное описание ординарных потоков отказов является наиболее простым при отсутствии последействия, когда вероятность появления отказов объектов в любом интервале наработки (t1, t2) не зависит от появления отказов в других интервалах наработки, непересекающихся с рассматриваемым интервалом.

Для ординарных без последействия (пуассоновских) потоков отказов вероятность безотказной работы объекта в интервале (t1, t2)

Принято считать, что пуассоновский поток отказов характерен для сложных нерезервированных систем, состоящих из высоконадежных элементов, потоки отказов которых являются независимыми. Если система "хорошо спроектирована", то нет отдельных малонадежных элементов, значения параметра потока отказов которых соизмеримы со значениями параметра потока отказов всей системы. Для такой системы появление отказов на одном интервале наработки почти не влияет на вероятность появления какого-либо числа отказов на другом интервале, не пересекающемся с первым.

При стационарном (ω = const) потоке отказов без последействия вероятность безотказной работы в интервале Δt

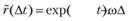
Иногда допущение об отсутствии последействия является слишком грубым. Тогда в качестве моделей реальных потоков отказов могут рассматриваться потоки отказов с ограниченным последействием, в которых значения наработки между последовательными отказами являются независимыми случайными величинами. Ограниченное последействие проявляется в том, что вероятность появления отказа за наработку (t1, t2) зависит от наработки, накопленной от последнего отказа, и не зависит от того, когда произошли предыдущие отказы.

Если случайные величины наработки между отказами одинаково распределены и независимы, то параметр потока отказов связан с плотностью распределения наработки между отказами f(t) уравнением

(5.6)

Это уравнение может быть получено путем следующих рассуждений. Пусть при отказе объекта он мгновенно восстанавливается, приобретая свойства нового объекта (или заменяется на новый). Среднее количество отказов (замен) п в интервале (t, t + dt) пропорционально числу N находящихся под наблюдением объектов и продолжительности интервала наработки dt

где п1 – количество отказов объектов из числа безотказно проработавших на интервале (0, t); п2 – количество отказов объектов из числа уже отказавших ранее.

Очевидно, что

Для определения среднего количества отказов объектов из числа уже отказавших ранее возьмем малый интервал наработки (τ, τ + dτ), предшествующий t. В течение этого интервала отказало и заменено на новые объектов. Из них в интервале (t, t + dt) будут вновь заменены. Суммируя по всем τ от 0 до t, получаем, что всего из числа уже отказавших (смененных) до момента времени t объектов вновь откажут на интервале (t, t + dt)

Общее среднее количество отказов на интервале наработки (t, t + dt)

При сокращении на Ndt получаем уравнение (5.6).

Таким образом, параметр потока отказов связан с плотностью распределения наработки между отказами интегральным уравнением Вольтерра второго рода с разностным ядром. Это уравнение не всегда удается решить в конечном виде. В некоторых случаях удобно искать решение, пользуясь преобразованием Лапласа. При этом

где – преобразование Лапласа функции ω(t) комплексной переменной s; – преобразование Лапласа функции f(t).

В общем случае уравнение (5.6) интегрируется численно. При этом можно использовать метод последовательных приближений, согласно которому выполняются последовательные вычисления по формуле

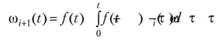
до тех пор, пока значения ωi(τ) и ωi+1(τ) не етанут практически совпадать. В качестве нулевого приближения удобно брать интенсивность отказов λ(t).

Если наработка между отказами имеет показательное распределение , то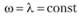

В технических заданиях на проектируемые объекты часто используют средний показатель

где tp – технический ресурс объекта.

Если при плотность распределения наработки до отказа , то существует установившееся значение параметра потока отказов

где – наработка на отказ ремонтируемого объекта (в рассматриваемом случае совпадает со средней наработкой до отказа )•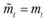

В общем случае наработка на отказ – отношение наработки ремонтируемого объекта к математическому ожиданию числа его отказов в течение этой наработки. Часто используется в качестве самостоятельного показателя надежности. Если наработка выражается в единицах времени, то может применяться термин "среднее время безотказной работы".

При нормальном распределении наработки между отказами параметр потока отказов равен

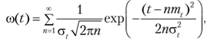
где – среднее значение и среднее квадратическое отклонение наработки между отказами соответственно.

На рис. 5.10 значения параметра потока отказов совершают ряд колебаний, прежде чем станут равными . Продолжительность этого колебательного процесса обратно пропорциональна среднему квадратическому отклонению наработки между отказами . Чем меньше , тем определеннее отказы группируются около средних значений и тем бо́льшая суммарная наработка должна накопиться, прежде чем сравняются условия появления отказов. При отказы происходят регулярно, и установившееся значение вообще не достигается.

Рис. 5.10. Параметр потока отказов объектов:

а – при нормальном распределении; б – при α-распределении наработки до отказа, α = 2, β = 500 ч (β – величина относительной долговечности в α-распределении Г. В. Дружинина [16, с. 193])

Таким образом, если рассматриваемый интервал наработки выбран достаточно далеко от начала эксплуатации объектов данного типа, то параметр потока отказов можно считать стационарным.

Начальные (при t = 0) и установившиеся (при ) значения параметра потока отказов при некоторых наиболее употребительных распределениях наработки между отказами приведены в табл. 5.19

Таблица 5.19

Значения параметра потока отказов при некоторых наиболее употребительных распределениях наработки между отказами

Распределение	Параметры распределения	Начальное значение	Установившееся значение
Показательное	λ	λ	λ
Нормальное		0
Редея	σ	0	0,797/σ
Гамма-распределение		0
Альфа-распределение
Распределение χ2-квадрат		0
Вейбулла		0
Суперпозиция показательных pacпределений

Вычисление условных распределений наработки между отказами становится необходимым при наличии в потоке отказов значительного последействия. Такой путь оценки надежности может применяться для изнашивающихся ремонтируемых объектов. Он появился в результате рассмотрения особенностей эксплуатации таких объектов. Эти особенности не учитываются при рассмотрении потоков отказов без последействия и с ограниченным последействием.

Многие типы ремонтируемых объектов за время эксплуатации отказывают ограниченное число раз (не более 3–5). Некоторые экземпляры объектов могут вообще нс отказывать в течение ресурса (срока службы). Если конкретный экземпляр объекта начинает часто отказывать, его снимают с эксплуатации.

Отличительной особенностью изнашивающихся ремонтируемых объектов является наличие коррелированных отказов. Иначе говоря, наработка между i-м и (i + 1)-м отказами коррелирует с наработкой до i-го отказа. При этом распределение наработки между отказами все время изменяется по мерс износа объектов. Любая профилактика, любой ремонт вызывают изменение корреляции между отказами. Поэтому целесообразно технический ресурс (срок службы) объектов разделить на периоды между крупными профилактическими мероприятиями и вычислять для каждого периода свои показатели надежности.

При вычислении условных распределений наработки между отказами можно отсчитывать наработку от момента окончания соответствующего ремонта или крупного профилактического мероприятия.

Показатели надежности в рассматриваемом случае те же, что и для неремонтируемых объектов, но они являются условными, т.е. вычисляются при условии, что произошло определенное число отказов. Эти показатели надежности характеризуют распределение случайной величины – наработки между i-м и (i + 1)-м отказами.

Если с увеличением суммарной наработки наблюдаются все более "серьезные" отказы, то иногда целесообразно рассматривать ремонтируемый объект как неремонтируемый и находить несколько распределений наработки до отказа, соответствующих различным определениям неработоспособного состояния, например:

• распределение наработки до первого отказа;

• распределение наработки до мелкого ремонта;

• распределение наработки до среднего ремонта;

• распределение наработки до капитального ремонта и т.д.

Показатели надежности ремонтируемых и восстанавливаемых объектов в процессе их применения вычисляются лишь в календарном времени. Восстанавливаемые в процессе применения ремонтируемые объекты можно разделить на две группы.

К первой группе относятся объекты, для которых в течение заданного времени работы допускаются отказы и вызванные ими кратковременные перерывы в работе. Для объектов этой группы большое значение имеет свойство готовности – способности находиться в процессе эксплуатации максимальное время в работоспособном и готовом к применению состоянии.

Ко второй группе относятся объекты, отказы которых в течение заданного времени недопустимы. Если в этих объектах (системах) имеются избыточные элементы, то при отказах некоторых из них объект остается работоспособным и можно проводить ремонт отказавших элементов во время выполнения задачи.

Один и тот же объект может быть отнесен к разным группам в зависимости от режима его применения.

Рассмотрим процесс эксплуатации объектов первой группы (рис. 5.11).

После отказа объект некоторое время находится в неработоспособном состоянии, т.е. ремонтируется. В результате ремонта объект приводят в работоспособное состояние. Возможные периоды выключения объекта, когда он не отказывает и не восстанавливается, исключаются из рассмотрения.

Таким образом, для первой группы объектов в процессе эксплуатации чередуются случайные периоды времени безотказной работы t(i) и времени восстановления (ремонта) tв(i). Обычно полагают, что случайные величины t(i) имеют одинаковые распределения (аналогично и tв(i)). Случайное время между очередными восстановлениями равно

Рис. 5.11. Реализация случайного процесса эксплуатации ремонтируемого восстанавливаемого объекта первой группы

[15, с. 40-43]:

t(1), ..., t(n) – значения времени работы между отказами; tВ(i), ..., tВ(n) – значения времени восстановления (ремонта); t0(i) – значение времени между (i – 1)-м и i-м восстановлениями; t1, ..., tn – моменты времени появления отказов (обозначены крестиками); – моменты времени восстановления (обозначены кружками)

Если случайные величины t и tu независимы, то плотность распределения их суммы t0 по известному из теории вероятностей правилу о композиции распределений равна

где f(t) – плотность распределения времени безотказной работы; g(t) – плотность распределения времени восстановления (ремонта) объекта.

По аналогии с ремонтируемыми невосстанавливаемыми в процессе применения объектами можно рассматривать поток восстановлений (уравнение восстановления – уравнение Вольтерра) с параметром

где – плотность распределения времени между очередными восстановлениями.

Параметр потока восстановленийи плотность распределения времени до появления i-го восстановления (это время равно сумме ) связаны соотношением

Надежность объектов первой группы может быть оценена с помощью мгновенных и числовых показателей. Одним из мгновенных показателей является параметр потока восстановлений . Однако обычно применяют вероятность застать объект работоспособным (готовым к применению) в момент времени ti либо вероятность того, что объект в момент времени ti будет неработоспособным (будет находиться в состоянии вынужденного простоя). Зависимость называется функцией готовности.

Как , так инаходятся в предположении, что при t = 0 объект работоспособен, т.е. Г(0) = 1, П(0) = 0.

Объект может находиться в момент времени t в работоспособном состоянии при осуществлении одного из двух несовместных событий:

• объект в течение времени (0, t) не отказал;

• объект отказывал и восстанавливался, и после последнего восстановления больше не отказывал.

Вероятность Г(t) застать объект работоспособным в момент времени t равна сумме вероятностей появления указанных событий. Вероятность появления первого события равна вероятности безотказной работы 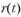объекта в течение времени (0, t).

Для определения вероятности появления второго события рассмотрим малый интервал, предшествующий t. Вероятность

того, что на этом интервале закончится последний ремонт и объект больше не откажет за оставшееся время (t – τ), равна

Суммируя по всем п = 1, 2, ..., получаем

где ω0(τ) – параметр потока восстановлений.

Интегрируя по τ от 0 до t, получаем вероятность того, что объект не откажет за время (t – τ), в виде

Таким образом, вероятность застать объект работоспособным в момент времени t равна

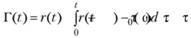(5.7)

Применим к формуле (5.7) узловую теорему восстановления (теорему Смита), т.е. поступим как и авторы [6, 12] – наши маститые корифеи в области надежности. Получается соотношение

где – математическое ожидание времени между очередными событиями потока; – невозрастающая интегрируемая в интервалефункция; – математическое ожидание числа

отказов в интервале (0, x).

Учитывая, что математическое ожидание для суммы случайных величин равно , получим выражение

(5.8)

Таким образом, вероятность Г(t) пристремится к установившемуся значению kг не зависящему от законов распределения случайных величин t и Величина kг часто отождествляется с коэффициентом готовности, который в ГОСТ 27.002–89 определяется как вероятность того, что объект окажется работоспособным в произвольный момент времени, кроме планируемых периодов, в течение которых использование объекта по назначению не предусматривается.

Согласно формуле (5.8) коэффициент готовности можно понимать как долю времени, в течение которого объект работоспособен, от общего времени эксплуатации объекта.

Учитывая общие свойства процесса восстановления, можно отметить особенность процесса приближения Г(t) к установившемуся значению kr при фиксированных значениях тt и . Стационарный режим наступает тем медленнее, чем меньше ди́сперсия случайной величины t0 = t + tв.

Часто используют среднее за срок службы tсл значение коэффициента готовности:

(5.9)

При этом

Рассуждая таким же образом, как и при выводе формулы (5.7), можно получить выражение для определения вероятности Г(t, t + τ) того, что объект не только окажется работоспособным в момент времени t, но и проработает безотказно на заданном интервале (t, t + τ) – иногда эту вероятность называют готовностью на промежутке (t, t + τ), или (с небольшой поправкой) оперативной готовностью:

(5.10)

Функцию готовности Г(£) можно рассматривать как частный случай функции Γ(t, t + τ) при τ = 0. При τ → ∞ функция Г(t, t + τ)

превращается в условную вероятность безотказной работы объекта, найденную в предположении, что в момент времени t объект работоспособен.

Установившееся значение будет равно

(5.11)

При произвольных законах распределения времени между отказами и времени восстановления при решении уравнений (5.10) и (5.11) возникают большие трудности. Могут быть использованы численные методы; иногда оказывается удобным операционный метод.

Наибольшее практическое значение имеет случай, когда время между отказами и время восстановления имеют показательные распределения:

(5.12)

где μ – интенсивность восстановления.

В результате решения уравнений (5.7)-(5.11) получим

(5.13)

(5.14)

(5.15)

(5.16)

Формулы (5.13)-(5.16) в основном используются при практических расчетах. Чтобы полнее и нагляднее раскрыть смысл коэффициента готовности, получим выражение (5.13), применяя приемы теории массового обслуживания.

При допущениях (5.12) процесс изменения состояний объекта будет марковским (т.е. без последействия) процессом с непрерывным временем и конечным множеством состояний: 0 – объект работоспособен; 1 – объект неработоспособен, находится в ремонте.

Найдем сначала вероятность того, что объект окажется работоспособным в момент времени t + Δτ. Для обозначения вероятностей нахождения в определенных состояниях в момент t будем применять буквы P(t) в отличие от вероятности безотказной работы в течение времени от 0 до t, обозначаемой r(t). Искомое событие может быть осуществлено двумя следующими несовместимыми способами:

• работоспособный к моменту времени t объект останется работоспособным в течение интервала времени (t, t + Δt);

• неработоспособный (находящийся в ремонте) к моменту времени t объект будет восстановлен в течение интервала времени (t, t + Δt).

Все остальные возможности имеют вероятность более высокого порядка малости, чем At.

Вероятность первого из указанных событий – вероятность застать объект в момент времени t в состоянии 0;– бесконечно малая но сравнению с At величина.

Так как сумма вероятностей состояний 0 и 1 равна = 1, то вероятность второго события будет

Следовательно, вероятность того, что к моменту времени t + At объект окажется работоспособным, равна

Отсюда заключаем, что

При имеем

(5.17)

Решив уравнение (5.17) для , получим формулу (5.13).

Если обозначить [15, с. 45]

то формулу (5.14) можно записать в виде

где – коэффициент простоя.

Когда , что обычно и бывает на практике,

На рис. 5.12 показана зависимость функции готовности Γ(t) от коэффициента. При увеличении надежность объекта снижается, но стационарный режим устанавливается более быстро. Если формулу (5.13) переписать в виде

то становится наглядно видно, что продолжительность переходного процесса определяется также величиной μ. Чем больше μ, тем быстрее наступает стационарное значение. Приводимые на рис. 5.12 графики соответствуют μ = 0,2 1/ч. Соответствующая зависимость для μ = 1,0 1/ч при р = 0,2 проведена на рис. 5.12 пунктиром. Пунктирная линия отображает резкий спад Γ(ί) и более быстрый выход на участок стационарности при μ = 0,2 1/ч, чем при μ = 1,0 1/ч [15, с. 46].

Рис. 5.12. Функция готовности Γ(t) при показательных распределениях времени безотказной работы и времени восстановления

При и значительных μ (системы с высоким уровнем безотказности и ремонтопригодности) продолжительность переходного процесса для Γ(t) определяется в основном значением μ. Формулу (5.13) можно преобразовать с учетом того, что

и значение kг определяется формулой (5.14):

Для объектов второй группы в качестве показателей надежности могут использоваться также параметр потока отказов, наработка на отказ и другие характеристики.

Рассмотрим способ пересчета средней наработки до отказа на различные условия применения объектов [15, с. 50–511 с учетом разброса значений параметров режимов работы или хранения. Способ основан на применении понятия случайной функции случайной нагрузки.

Случайная наработка до отказа объекта зависит от двух групп факторов: характеристик качества (внутренние факторы) и характеристик режима работы или хранения (внешние факторы).

Режим работы или хранения объекта целесообразно оценивать статистически. Одинаковая аппаратура может находиться в различных условиях применения. Например, оборудование однотипных самолетов может испытывать различные случайные температурные и механические воздействия. Установленные в разных точках одной системы одинаковые элементы также находятся в различных режимах, например при разной температуре. Можно привести еще ряд соображений о случайном характере параметров режима работы или хранения элемента, взятого наугад из группы одинаковых элементов системы. В большинстве случаев для не очень больших периодов эксплуатации случайную нагрузку можно представить в виде суммы случайной величины, характеризующей общие условия, в которых эксплуатируется объект, и стационарной случайной функции времени, характеризующей стабильность этих условий эксплуатации. Будем учитывать лишь окончательные отказы, возникающие в результате накопления необратимых изменений в деталях технического объекта (хотя эти изменения иногда внешне незаметны). Для приближенного исследования влияния режимов работы на надежность объектов колебания нагрузок учитываться не будут, т.е. предполагается, что для рассматриваемого периода эксплуатации нагрузка является случайной величиной.

Иногда разброс значений параметров режимов работы или хранения технических объектов настолько мал, что эти характеристики можно считать неслучайными величинами или процессами. Например, устройства могут храниться в помещении с автоматически регулируемой температурой и влажностью. Другим примером практически неслучайного режима работы объектов могут служить их лабораторные испытания.

Технические объекты не могут обладать одинаковой сопротивляемостью внешним воздействиям. На их качество влияет распределение внутренних напряжений, скрытые дефекты внутренней структуры материалов, случайные колебания технологии изготовления и другие случайные причины. Поэтому при одинаковых нагрузках наработка до отказа одинаковых объектов будет различной. Для взятого наугад объекта из группы одинаковых, работающих при фиксированной нагрузке, наработка до отказа является случайной величиной. При изменяющейся неслучайной нагрузке наработку до отказа можно рассматривать как случайную функцию нагрузки. Таким образом, необходимо оценивать статистически как режим работы объектов, так и их реакцию на режим работы.

В настоящее время при вероятностных исследованиях используются два вида зависимостей: случайные функции и функции случайных аргументов. Для случайной функции характерна случайная связь между неслучайной и независимой переменной и зависимой переменной. У функции случайного аргумента неслучайная зависимость связывает случайный аргумент с зависимой переменной. Физические особенности процесса существования технических объектов определяют необходимость введения понятия случайной функции случайного аргумента. Для этого вида зависимости характерна случайная связь между случайным аргументом и зависимой переменной. Подробное изложение теории восстанавливаемых систем с учетом изменения законов распределения отказов дано в целом ряде книг.