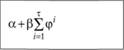Модели экспоненциального сглаживания
Универсальной формулы для вывода дисперсии для всех моделей экспоненциального сглаживания не существует, поэтому их нужно рассматривать по отдельности. В зависимости от учета ошибок, а также типа тренда все модели ETS можно разделить на классы[1], представленные в табл. 9.1.
Таблица 9.1
Классы моделей по методу расчета дисперсии
|
Класс модели |
Тип сезонности |
||
|
N |
A |
Μ |
|
|
Класс 1 |
Λ,Ν,Ν Α,Α,Ν AAd,N |
Α,Ν,Α A,A,A A,Ad,A |
|
|
Класс 2 |
Μ,Ν,Ν M,A,N Μ,Αd,Ν |
Μ,Ν,Α Μ,Α,A Μ,Αd,A |
|
|
Класс 3 |
Μ,Ν,Μ Μ,Α,Μ Μ,Αd,,Μ |
||
|
Класс 4 |
Μ,Μ,Ν Μ,Μd,Ν |
М,М,М Μ,Μd,Μ |
|
|
Класс 5 |
Α,Μ,Ν Α,Μd,Ν |
Α,Μ,A A,Μd,A Μ,Μ,Α M,Md,A |
Α,Ν,Μ Α,Α,Μ Α,Αd,Μ A,M,Μ Α,Μd,Μ |
Классы объединяются по следующему принципу:
1. Класс 1 – линейные модели с аддитивной ошибкой.
2. Класс 2 – линейные модели с мультипликативной ошибкой.
3. Класс 3 – модели с линейным трендом, но мультипликативной ошибкой и сезонной компонентой.
4. Класс 4 – модели с мультипликативной ошибкой и трендовой компонентой и либо без сезонности, либо с мультипликативной сезонностью.
5. Класс 5 – тяжело оцениваемые модели с сочетанием аддитивных и мультипликативных элементов.
Аналитические формулы для дисперсии можно вывести только для моделей первых трех классов. Для последних двух классов рекомендуется пользоваться непараметрическими методами. Модели класса 5 могут вызывать численные сложности при построении долгосрочных точечных прогнозов.
Рассмотрим, как можно рассчитать дисперсию для моделей из первого класса, на примере модели Брауна.
В соответствии с формой коррекции ошибок из табл. 7.6 будущее значение yt по ETS(Α,Ν,Ν) на h шагов вперед может быть записано в виде
Чтобы корректно рассчитать дисперсию, далее делается предположение о том, что модель (9.20) лежит в основе процесса, а значит, вплоть до шага h уровень будет адаптироваться к ошибкам. Первое уравнение из системы переписывается в виде
Теперь подставим в (9.21) вместо lt+h_1 значение, рассчитанное по второму уравнению из системы (9.20):

Продолжая итеративно подставлять вместо It расчетные значения, полученные на основе второго уравнения в (9.20), получим
 (9.22)
(9.22)
Затем рассчитаем условную дисперсию (9.22) с учетом наших базовых предположений:
 (9.20)
(9.20)
 (9.21)
(9.21)
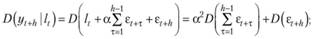
 (9.23)
(9.23)
Формула (9.23) считается наиболее корректной для расчета дисперсии в модели Брауна. Использование вместо нее просто дисперсии ошибок некорректно, так как такое допущение не учитывает структуру экспоненциального сглаживания.
На основе полученной дисперсии можно легко рассчитать прогнозный интервал для модели Брауна:
 (9.24)
(9.24)
Рассмотрим, каким получится прогнозный интервал для метода Брауна на примере ряда № 41. Мы уже делали точечный прогноз для этого ряда, на рис. 9.7 показаны точечный и интервальный прогнозы по модели Брауна с первым методом задания стартового значения.

Рис. 9.7. Ряд данных № 41 (сплошная линия с точками), точечный (сплошная линия) и интервальный (пунктирные линии) прогнозы по нему, полученные по методу Брауна
Можно обратить внимание на то, что первое прогнозируемое фактическое значение не попало в доверительный интервал, хотя верхняя граница оказалась достаточно близко к нему. Все же остальные значения, вплоть до значения на 1994-й г., оказались лежащими внутри интервала. Правда, сам интерват оказался очень широким, таким, что границы на 1994-й г. получились (2284; 8589). Однако, если бы он был у́же, то, скорее всего, некоторые значения просто не попали бы в него. Здесь мы сталкиваемся с классической проблемой: в слишком узкие интервалы попадает меньшее число значений, что приводит к недооценке показателя, в то время как слишком широкие границы не несут полезной информации.
Дисперсии по другим моделям класса 1 выводятся по аналогии с дисперсией для модели Брауна. В табл. 9.2 приведены параметры, позволяющие рассчитать дисперсию для каждого из методов классов 1 и 2.
Таблица 9.2
Параметры методов классов 1 и 2, использующиеся при расчете дисперсии
|
Модель |
Ст |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Примечание: dτ = 1, если τ = 0 и dτ = 0 во всех остальных случаях.
Для расчета дисперсии моделей класса 1 используется формула
 (9.25)
(9.25)
Можно заметить, что дисперсия для моделей класса 1 зависит от срока прогнозирования. Причем если в модели есть трендовая компонента, то эта зависимость носит нелинейный характер – интервалы в таком случае будут быстрее расширяться, нежели в случае отсутствия такой компоненты.
Из-за того, что мультипликативная модель экспоненциального сглаживания отличается от аддитивной лишь формой ошибки, параметры, приведенные в табл. 9.2, могут быть с успехом применены для расчета дисперсий моделей класса 2. Однако, очевидно, что сама формула должна отличаться от (9.25)[2]:
 (9.26)
(9.26)
где
 (9.27)
(9.27)
Как мы уже обсуждали, аддитивная модель отличается от мультипликативной лишь тем, как строится доверительный интервал – точечные прогнозы в них абсолютно идентичны.
Посмотрим на примере ряда № 41, как различаются интервальные прогнозы по модели ETS(A,N,N) и ETS(М,N,N) (рис. 9.8).

Рис. 9.8. Ряд данных № 41 (сплошная линия с точками), точечный (сплошная линия) и интервальный (серые области, соответствующие 95% и 80%) прогнозы по нему, полученные по методу Брауна
Как видим, интервалы, построенные для модели с мультипликативной ошибкой, оказались значительно шире интервалов по модели с аддитивной ошибкой, причем, в общем-то, неоправданно шире – уже на 1992 г. нижняя граница уперлась в отметку "О", а верхняя перевалила за 10 000, что совершенно не информативно, учитывая точечный прогноз примерно в 5500. Однако, если в данном случае прогнозный интервал по модели Брауна получился слишком широким, это не говорит о том, что для другого ряда с другой моделью он так же будет шире интервала с аддитивной ошибкой. В каждом конкретном случае нужно принимать индивидуальное решение о том, какую модель выбрать.
Последний класс моделей экспоненциального сглаживания, для которых мы рассмотрим метод построения параметрических прогнозных интервалов, – это модели класса 3. Дисперсия для этих моделей должна учитывать мультипликативную сезонную составляющую и рассчитывается так, как это показано в табл. 9.3.
Таблица 9.3
Параметры методов класса 3, использующиеся при расчете дисперсии
|
Модель |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Как видим, значения введенного параметра cj для моделей класса 3 совпадает со значениями для первых трех моделей классов 1 и 2. В столбце  приведены формулы для расчета прогнозов по трендовой компоненте.
приведены формулы для расчета прогнозов по трендовой компоненте.
Формула расчета дисперсии для методов класса 3 выглядит несколько сложнее формулы (9.26) и имеет вид
 (9.28)
(9.28)
где
 (9.29)
(9.29)
Стоит заметить, что с помощью формул (9.28) и (9.29) для прогноза на период h > s можно получить лишь приблизительную оценку дисперсии. Более точные формулы более громоздки, однако при этом не дают значительного повышения точности прогноза.