Многокритериальная постановка задачи принятия управленческих решений
Методов многокритериальной оптимизации существует достаточно много. Это вызвано большим количеством прикладных задач, включающих в себя суть комплексной оценки ситуации. Пусть дай n-мерный вектор параметров X, характеризующий исследуемую ситуацию, относительно которой принимается решение:
(5.39)
Вектор X может представлять собой инвестиции предприятия в различные сферы деятельности, выделенные трудовые и иные ресурсы, факторы стимулирования труда сотрудников и пр.
Примем также, что ситуация анализируется (оценивается) с помощью m-критериев
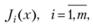(5.40)
для каждого из которых требуется найти максимум на множестве допустимых ситуаций G. Это требование нс является жестким. Критерий на "min" можно легко обратить в критерий на "шах" путем изменения знака соответствующего выражения в (5.40).
Критериями являются показатели роста и развития экономической системы. В ряде случаев кроме критериев задаются ограничения, при выполнении которых необходимо достичь экстремальных результатов.
Это общая постановка задачи многокритериальной оптимизации.
В качестве примера можно привести задачу на определение объемов выпуска продукции предприятия, при которых будет достигаться максимум прибыли и минимум себестоимости.
Возможны случаи, когда поставленная математическая задача не имеет решения. Действительно, в приведенном примере точка в признаковом пространстве (5.39), в которой достигается максимум прибыли, никогда не совпадает с точкой, в которой минимальна себестоимость продукции. То есть математические решения в ряде случаев не могут описать адекватно ситуацию принятия решений. Это актуализирует проблему решения многокритериальных задач. Существует два основных подхода к се решению:
• сведение многокритериальной задачи к однокритериальной;
• параллельный учет нескольких критериев.
Сведение многокритериальной задачи оптимизации к однокритериальной задаче. Данный подход опирается на различные способы постановки и решения многокритериальных задач, исходя из определенного компромисса между частными критериями. Пусть необходимо найти
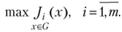(5.41)
Идея компромисса заключается в том, что строится некая функция, зависящая от заданных частных критериев
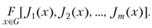(5.42)
Относительно этой функции, учитывающей значения частных критериев, строится задача оптимизации. Причем правило построения этой функции лежит в сфере прикладной экономики. Таким образом, строится функция, аргументами которой являются исходные критерии. Выбором вида критериальной функции занимается ЛПР, а не математики. Последние могут давать рекомендации ЛПР для принятия решения.
Рассмотрим три наиболее распространенных на практике и наиболее простых с точки зрения содержательной интерпретации случая.
Задача 5.13. Если у ЛПР есть уверенность, что какой-то из критериев является самым важным по содержанию (например, первый), то остальные игнорируются и решается задача:
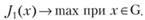
То есть полагается:
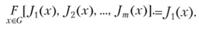
Но такие содержательные ситуации, когда можно выделить подавляющий критерий, встречаются весьма редко. Чаще может быть так, что среди заданных m-критериев есть главный критерий, но остальные не учитывать нельзя.
Из этих рассуждений следует второй случай.
Задача 5.14. Задача многокритериальной оптимизации преобразуется следующим образом: главный критерий максимизируется, а на остальные накладываются ограничения (так урезается множество допустимых значений).
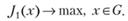(5.43)
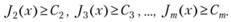(5.44)
С2, ..., Сm – те значения экономических показателей, которые должны быть обязательно достигнуты. Например, достижение максимальной прибыли при заданной себестоимости продукции.
Таким образом, надо найти такое решение, при котором главный критерий максимизируется, но вводятся дополнительные ограничения: что значения остальных критериев должны быть не хуже тех показателей, которые обеспечивают нормальное функционирование экономической системы.
Третий случай.
Задача 5.15. На практике могут возникать ситуации, когда трудно даже проранжировать локальные критерии. Это происходит из-за того, что локальные критерии объективно равнозначны, или потому, что ЛПР (иногда объективно, а иногда и в силу некомпетентности) не может определить главный критерий. В этих случаях используется свертка критериев. Различают аддитивную и мультипликативную свертки. Простейшей из них является линейная, аддитивная свертка. Она определяется следующим выражением:
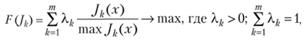(5.45)
где λk – весовые коэффициенты, относительные значимости локальных критериев.
Если все локальные критерии имеют одинаковую значимость, то каждое λk= 1 /т. Тогда их можно вынести за знак суммы и сократить, так как они не меняют точки максимума.
Знаменатель представляет собой нормирующий множитель – это результаты решения k-й задачи по оптимальному k-му локальному критерию при полном игнорировании остальных. В этом случае все слагаемые будут не более единицы и безразмерными величинами. Это важно, так как локальные критерии оптимальности могут иметь разную размерность (например, денежные единицы, временны́е единицы, проценты). Для получения знаменателей дроби надо сначала решить локальные задачи, а потом поставить многокритериальную.
Таким образом, третий подход достаточно трудоемок, но он наиболее гибок, поскольку позволяет варьировать важностью каждого локального критерия.
Мультипликативная свертка оперирует произведением степеней частных критериев. Характерным примером мультипликативной свертки является производственная функция предприятия, представляющая собой взвешенное произведение трудового и финансового капитала предприятия. Выбор типа свертки должен обосновываться. Мультипликативные свертки легко сводятся к аддитивным путем логарифмирования произведения частных критериев.
Выбор вида свертки – сложная задача, требующая хорошего понимания сущности исследуемого процесса. Если ЛПР склонен относительно применения частных критериев опираться на союз "или" (решение принимается, если или первый критерий выполняется, или второй, или... и т.д.), то адекватнее использовать аддитивную свертку критериев. Если связующим является союз "и" (решение принимается, если и первый критерий выполняется, и второй, и... и т.д.), то правильнее принять мультипликативную свертку критериев.
Преимуществом свертки критериев является упрощение задачи анализа за счет сведения ее к однокритериальной постановке. Недостаток кроется в неоправданной в ряде случаев компенсации одних эффектов другими, невозможности разделить и сравнить эти эффекты.
Процедуры учета многих критериев. Рассмотрим ряд методов второго подхода, при котором осуществляется параллельный учет нескольких критериев.
1. Наиболее известным из этих методов является метод Парето, который определяет множество так называемых нс улучшаемых (хотя бы по одному из частных критериев) решений. Если необходимо оперировать только одним вариантом решения, то он определяется из дополнительных соображений. Например, вводится дополнительный критерий, не включенный в состав первоначально анализируемых показателей. Рассмотрим идею метода, ориентируясь на два частных критерия: прибыль предприятия Р и себестоимость S его продукции (рис. 5.7).
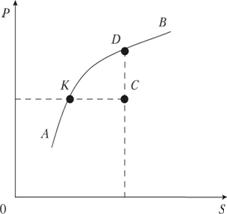
Рис. 5.7. Графическая иллюстрация метода Парето:
Точки плоскости S0P характеризуют различные, сравниваемые между собой ситуации, в которых может находиться предприятие. Ситуация, описываемая точкой С, улучшается, с одной стороны, ситуацией D (при одинаковой себестоимости прибыль выше), с другой стороны, ситуацией К (при одинаковой прибыли себестоимость ниже)
Все возможные решения об объемах и видах выпускаемой продукции, установленном качестве, изменении технологии выпуска и др. в пространстве критериев SOP изображаются точками, координаты которых соответственно равны значениям выбранных критериев.
Решение, соответствующее на рис. 5.7 точке С, относится к разряду улучшаемых по обоим указанным критериям. Все решения, соответствующие части KD кривой АВ, ограничивающей все множество допустимых решений, лучше, чем С, и являются подмножеством Парето. Если имеется формальное выражение заданных критериев Р и 5, то легко получить аналитическую зависимость для кривой АВ, на множестве точек которой и будет по дополнительному критерию отыскиваться рекомендуемое для исполнения решение. В противном случае множество точек (решений) получается:
• статистическим путем в результате наблюдения прошлого опыта функционирования предприятия;
• на основе имитации деятельности, при "прокручивании" сценариев развития по моделям;
• на основе экспертного анализа.
2. Максиминный подход к решению многокритериальной задачи. Существенной особенностью всех рассмотренных выше постановок решения многокритериальных задач является необходимость формирования четко определенных функций критериев Ji(X). Для социально-экономических задач хорошо иллюстрируется проблемность такого подхода. Действительно, пусть в качестве критериев рассматриваются следующие показатели: конкурентоспособность, инновационность, креативность (предприятия или субъекта) и т.д. Невозможно не только задать аналитические выражения для этих показателей, но и указать перечень параметров (табл. 5.8), от которых они зависят.
Принятие решений с помощью излагаемой ниже максиминной стратегии основывается на предположении, что количество критериев J, относительно которых принимается решение, и число возможных вариантов решения V ограничены и заранее известны. В этом случае полное условие задачи задается матрицей (см. табл. 5.8).
Таблица 5.8
Исходные данные максиминной стратегии принятия решений
|
Vj / Ji |
V1 |
V2 |
… |
Vn |
|
J1 |
a11 |
a12 |
… |
a1n |
|
… |
… |
… |
… |
… |
|
Jm |
am1 |
am2 |
… |
amn |
|
mini |
ax1 |
aj2 |
… |
ahn |
Анализируя табличные данные по столбцам, выбираем для каждого из них минимальный элемент, т.е. наиболее критичный показатель-критерий. И наконец, в этой строке отбираем максимальное значение, т.е. вариант с наибольшим значением критерия. Полученное решение обладает гарантированными свойствами: максимизация наихудшего показателя:
Vopt = arg maxj mini aij. (5.46)
Ключевые значения параметров алгоритма – коэффициенты аij определяются на основе анализа априорных данных об исследуемой ситуации, если она имеет четкую и известную структуру, статистически – в противном случае. Последний вариант реализуем, если существует достоверная, репрезентативная информация о функционировании исследуемого объекта.
3. Принятие решений с помощью композиции нечетких множеств обобщает предыдущий метод, снимая ограничения на наличие четкой и известной структуры затрат и прибылей от реализации возможных вариантов, а также на наличие репрезентативной информации о функционировании исследуемого объекта. Неизвестные коэффициенты рассматриваются в этом случае в качестве функций принадлежности нечетких множеств:
• степень выполнения критериев для заданного варианта решения, если рассматриваются столбцы табл. 5.8;
• степень соответствия варианта решения заданному критерию, если рассматриваются строки таблицы.
Указанные функции принадлежности задаются экспертами, и метод может реализовываться не только для существующих, но и для гипотетических (разрабатываемых) систем.
Таким образом, использование теории нечетких множеств является для целого класса решаемых в экономике задач наиболее предпочтительным, а в ряде случаев и единственно возможным.
4. Метод максимальной алгоритмической надежности. В данном методе вместо требования максимизации критериев предлагается ввести некоторые численные значения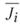 
заданных критериев Ji, допустимые и удовлетворительные по техническим и технологическим условиям, и решать задачу:
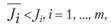(5.47)
которая для каждого конкретного i определяет множество допустимых стратегий Si.
Обоснованием данного подхода являются следующие соображения: критерии Ji определяются статистически и (или) по экспертным данным, по ограниченному (и, как правило, нестационарному и субъективному) набору данных. Структура искомых зависимостей априори неизвестна, поэтому точность идентификации J: невелика, и решение классических задач оптимизации будет некорректным.
На основании формулы (5.47) определяется i областей Si, каждая из которых ограничивает множество допустимых стратегий управления по соответствующему критерию. Пересечение этих областей определяет "трубку решений" – множество стратегий S0, допустимых по всем критериям (рис. 5.8).
В качестве основного критерия J0 на S0 предлагается критерий максимальной алгоритмической надежности, суть которого состоит в том, что выбирается та стратегия, которая при возможных прогнозируемых отклонениях хода технологического процесса с минимальной вероятностью приведет к нарушению условия (5.47). Этому критерию, очевидно, удовлетворяет ось "трубки решений" Sопт.
Проиллюстрируем приведенные рассуждения конкретным примером, расширяя условия задачи 5.2, приведенной в параграфе 5.1.
Как правило, фирма заинтересована в улучшении всех показателей (в нашем случае и прибыли, и себестоимости), т.е. возникает задача согласования противоречивых критериев. Классическая теория оптимальных решений предлагает целый спектр процедур для решения этой задачи.
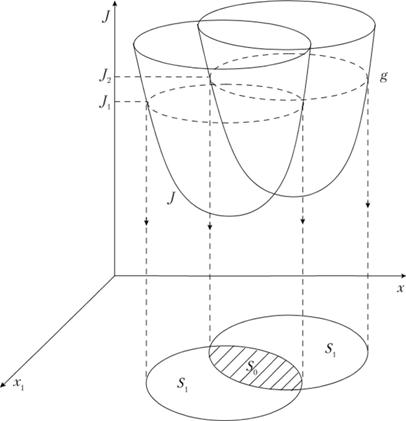
Рис. 5.8. Геометрическая иллюстрация способа построения области допустимых решений
Ниже использован подход, учитывающий стратегические и тактические задачи фирмы. Выбор метода определялся следующими соображениями. Стратегическая задача фирмы – выживание, а оно возможно, если прибыли, например, получено не менее чем 250 усл. ед. (средства, необходимые на покрытие всевозможных расходов), а себестоимость не выше, чем 4,07 ед. (ограничение на затратность производства, вытекающее из условий конкурентной борьбы). Кроме того, исходные данные (см. табл. 5.1), очевидно, заданы с ошибкой, процессы производства и реализации товара нестационарны, а условия применения методов моделирования не выполняются в полном объеме, т.е. модели (5.4)-(5.6) могут быть неадекватными реальным процессам. В силу вышесказанного полного доверия к точкам х1 и х2 нет. Метод согласования критериев, используемый ниже, учитывает недостоверность и неточность исходных данных. Смысл его заключается в следующем.
1. Вместо критериев шах J1 и min J2 устанавливается система ограничений:
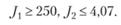(5.48)
2. Подставляя данные из формул (5.48) в (5.5) и (5.6), получаем для исследуемого х два промежутка: [125,5; 267,5] и [62,2; 137,8].
3. Определяется общая область этих промежутков, т.е. множество всех х, для которых удовлетворяются требования и по прибыли, и по себестоимости. Это закрытый интервал [125,5; 137,8]. Его границы так же ненадежны, как и точки экстремумов, найденные выше.
4. Выбираем в качестве оптимального решения середину последнего промежутка – точку, наиболее удаленную от границ промежутка, а следовательно, наиболее защищенную от непредсказуемых возмущений среды и (или) ненадежности вычислительного алгоритма. Эта точка обеспечивает алгоритмическую надежность процедуры принятия решений.