Метод сценариев и value at risk

Метод сценариев. Сценарный анализ (scenario analysis) - это иной метод анализа рисков, по мнению многих, более корректно отражающий реальность.

В соответствии со сложившимся убеждением анализ чувствительности неверно отражает фактическую ситуацию, поскольку основан на предположении, что изменение одного параметра финансовой модели происходит независимо от остальных, а это не так. Например, рост объемов продаж сопровождается ростом затрат, налогов и т.п., и изменению подвергаются сразу несколько параметров.

При осуществлении сценарного анализа формулируются допущения и рассчитывается бюджет денежных потоков не для одного, а для трех-пяти возможных сценариев развития событий. При этом при изменении сценария могут измениться все параметры финансовой модели. Во-первых, такой подход дает возможность развернуто охарактеризовать потенциальные выгоды и убытки проекта (сопоставить по масштабу возможные выгоды с вероятными потерями). Во-вторых, он позволяет дать вероятностную характеристику проекту в целом.

Вероятностные характеристики проекта. Для расчета вероятностных характеристик проекта каждому из сценариев присваивается своя вероятность реализации (Pj). Затем рассчитываются интегральные характеристики проекта:

o математическое ожидание (NPV):

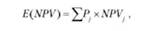
где NPV j - чистая приведенная ценность для j-ro сценария; o стандартное отклонение NPV:

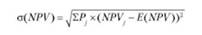
Пример. Для проекта "Дейтерий-1" разработаны пять сценариев дальнейшего развития событий (табл. 3.25).

ТАБЛИЦА 3.25. Сценарии развития проекта

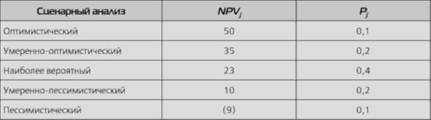
Требуется оценить ожидаемое значение и стандартное отклонение NPV данного проекта (табл. 3.26).

Решение.

ТАБЛИЦА 3.26. Расчет ожидаемого значения и стандартного отклонения NPV проекта

Сценарный анализ	NPVj	PJ	NPVjxPj	NPVj-Е [NPV)	Pjx(NPVj- E[NPV)f
Оптимистический	50	0,1	5	27,7	76,729
Умеренно-оптимистический	35	0,2	7	12,7	32,258
Наиболее вероятный	23	0,4	9,2	0,7	0,196
Умеренно-пессимистический	10	0,2	2	(12,3)	30,258
Пессимистический	(9)	0,1	(0,9)	(31,3)	97,969

E(MPV) = 22,3 млн руб.; a(NPV) = 15,41 млн руб.

Зная математическое ожидание и стандартное отклонение, строят кривую распределения для NPV (чаще всего это нормальное распределение). На основании этой кривой может быть найдена вероятность того, что NPV будет меньше нуля и одновременно доходность проекта окажется меньше ставки дисконта, принятой для расчета NPV (рис. 3.12). Поэтому в данном случае для оценки NPV можно взять не только стоимость капитала, но и любую другую ставку, вероятность падения ниже которой мы хотели бы оценить.

Ценность, подверженная риску (Value at risk, VAR). Такой подход оценивает "опасный" риск проекта, т.е. рассматривает риск с точки зрения возможности убытков, которые могут проистекать от принятого решения.

Аналогичный подход реализуется в известном показателе VAR (value at risk), отражающем, какой максимальный уровень потери ценности может проистекать из принятого инвестиционного решения. Естественно, суждение такого рода не может быть абсолютно достоверным и потому дается с некоторой (достаточно высокой) степенью доверительной вероятности (рис. 3.13).

Например, если бы хотелось оценить падение №У проекта ниже безрисковой или депозитной ставки банка, в сценарном анализе для оценки №РУ/ нужно было бы взять безрисковую ставку или ставку банка в качестве ставки дисконта.

В случае принятия гипотезы о нормальном распределении результирующего показателя (МРУ проекта) УАЛ можно рассчитать так:

УАР, = Е(ЫРУ) + г(а(ЫРУ)). (3.22)

Параметр 2 для 95%-ной доверительной вероятности равен -1,65.

Пример. Таким образом, для проекта "Дсйтсрий-1" (как мы помним, Е(ЫРУ) = 22,3 млн руб., а(ЫРУ) = 15,41 млн руб.) можно получить:

КЛ"=22,3 + (-1,65) х 15,41 = -3,13 млн руб.

Таким образом, с вероятностью 95% можно утверждать, что потери ценности от принятия инвестиционного решения не превысят 3,13 млн руб.

Рис. 3.13. Иллюстрация к концепции VAR