Метод нахождения максимального потока

При планировании рационального распределения продукции в сети распределения необходимо согласовывать пропускную способность каналов с потребностями клиентов и с мощностью производственного предприятия. Данный класс задач решается методом нахождения максимального потока.

Рассмотрим сеть распределения (рис. 4.21), в которой выделены пункты 0 (вход, например, склад готовой продукции производителя) и п (выход, распределительные центры, склады оптовых и розничных организаций, потребитель) и каждой дуге (отрезку), связывающей пункты i и j, сопоставлено число dij > 0, называемое пропускной способностью дуги. Величина пропускной способности характеризует максимальное допустимое количество материального потока, которое может проходить по соответствующей дуге в единицу времени.

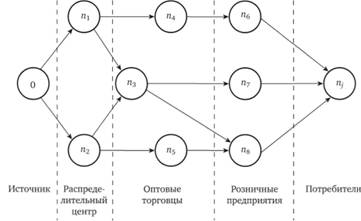
Рис. 4.21. Пример сети распределения

Количество продукции, проходящее по дуге от i до j, будем называть потоком по дуге (i,j) и обозначать через 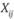. Очевидно, что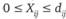

Если учесть, что весь материальный поток, вошедший в промежуточный пункт сети, должен полностью выйти из него, получим

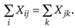
Из естественного требования равенства потоков на входе и на выходе имеем

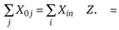
Величину Z назовем величиной потока в сети и поставим задачу максимизации Z при соблюдении обозначенных выше условий.

Поиск максимального потока сводится к поиску пропускной способности минимального разреза.

Рассмотрим универсальный алгоритм поиска в матричной форме.

Начальный этап алгоритма состоит в построении матрицы D0, в которую заносятся значения пропускных способностей (для неориентированной дуги берем симметричные значения элементов матрицы ).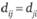

Основные шаги алгоритма состоят в поиске некоторого пути и коррекции потока на этом пути.

При поиске пути используем процесс отмечаний. Метим символом * нулевые строку и столбец матрицы (вход сети). В 0-й строке отыскиваем 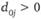, метим соответствующие столбцы индексами

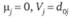
и переносим метки столбцов на строки. Затем берем ί-ю отмеченную строку, ищем в ней непомеченный столбец с 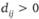, которому сопоставляем метки-индексы

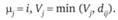
Метки столбцов переносим на строки, и этот процесс продолжаем до тех пор, пока не будет отмечен п-й столбец.

Затем "обратным ходом" по индексам выясняем путь, приведший к η-й вершине, уменьшаем пропускные способности дуг пути (элементы матрицы) на Vn и увеличиваем симметричные элементы на эту же величину.

Такая процедура продолжается до тех пор, пока отмечание n-й вершины не станет невозможным.

Максимальный поток может быть найден вычитанием из исходной матрицы D0, получаемой после приведенной выше корректуры матрицы пропускных способностей:

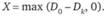
Пример 4.4

Производство размещено в Москве. Для распределения продукции предприятие привлекает посредников, которые работают с предприятием через распределительные центры различных уровней. В европейской части России работает оптовое предприятие 1, обслуживаемое центральным распределительным центром. Оптовое предприятие 2 работает в ближайшем зарубежье (Украина, Белоруссия) и обслуживается региональным распределительным центром. Есть у предприятия на местном рынке (Москва и Московская область) свои клиенты – ритейлеры, которые получают продукцию с городского распределительного центра. Запасы регионального и городского распределительных центров пополняются с центрального распределительного центра.

Выделим фрагмент распределительной сети:

• склад готовой продукции производственного предприятия;

• центральный распределительный центр;

• региональный распределительный центр;

• городской распределительный центр;

• два оптовых предприятия;

• розничная точка, принадлежащая компании;

• потребители.

Рис. 4.22. Сеть распределения производственного предприятия

Каждое звено сети распределения обозначим цифрой, а над дугами проставим пропускную способность. Пропускная способность в зависимости от вида звена может быть выражена через объем производственной мощности, плановую потребность (спрос) потребителей и емкость рынка.

Граф сети распределения продукции представлен на рис. 4.23. Построим матрицу D0, в которую занесем значения пропускных способностей звеньев распределительной сети (рис. 4.24).

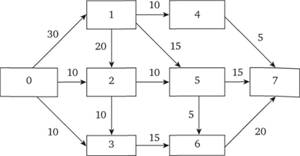
Рис. 4.23. Граф сети распределения производственного предприятия

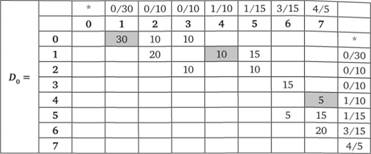
Рис. 4.24. Поиск оптимального решения: итерация 1

Из нулевой строки отметим вершины (строки-столбцы) 1, 2 и 3 индексами μ = 0 и V, равными 30,10 и 10.

Из помеченной строки 1 отметим вершины 4 и 5 индексами μ = 1 и V4 = min (30,15) = 15, V5 = min (30,10) = 10.

Из строки 3 отметим вершину 6 и, наконец, из строки 4 – вершину 7 (рис. 4.25).

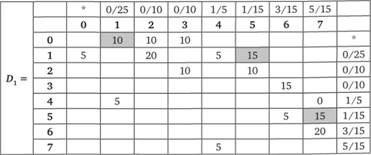
Рис. 4.25. Поиск оптимального решения: итерация 2

Обратным ходом по μ обнаруживаем путь: к вершине 7 от 4, к вершине 4 от 1, к вершине 1 от 0; корректируем элементы D0 на величину потока V7 = 15.

Очередной шаг дает путь [0-1-5-7] с потоком 5 (рис. 4.26).

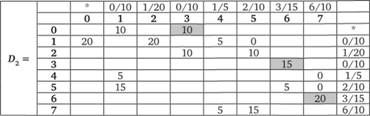
Рис. 4.26. Поиск оптимального решения: итерация 3

Последующий шаг дает результат, представленный на рис. 4.27.

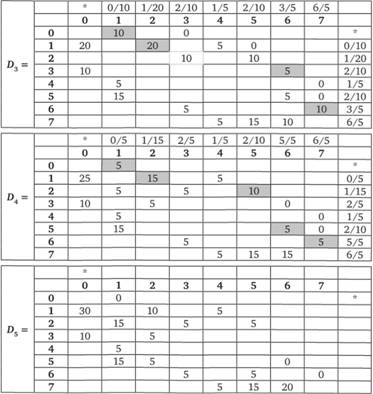
Рис. 4.27. Поиск оптимального решения: итерации 4, 5 и 6

Дальнейшее отмечание невозможно. Отсюда получаем матрицу максимального потока (рис. 4.28).

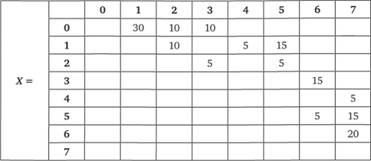
Рис. 4.28. Матрица максимального потока

В результате применения алгоритма нахождения максимального потока в сети получены результаты, представленные на рис. 4.29. Пары цифр в скобках, показанные на дугах графа, означают максимальную пропускную способность дуги и рекомендуемый объем поставки товаров в сеть.

Рис. 4.29. Результат расчета максимального потока при распределении продукции производственного предприятия