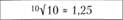Методы и виды стандартизации

Для достижения поставленных целей и руководствуясь установленными принципами, стандартизация может использоваться различные методы и приобретать при этом разнообразные формы.

Видами стандартизации являются параметрическая стандартизация, комплексная стандартизация, опережающая стандартизация.

Параметрическая стандартизация – это процесс стандартизации параметрических рядов, который заключается в выборе и обосновании целесообразной номенклатуры и численного значения параметров. Параметрический ряд – это набор установленных значений параметров объекта, составленный из предпочтительных чисел. Наиболее важными параметрами объекта являются размерные, эксплуатационные, энергетические, силовые параметры и параметры массы.

Параметрический ряд составляют из предпочтительных чисел.

Предпочтительные числа представляют собой систему параметрических десятичных рядов чисел, построенных по арифметической или геометрической прогрессиям.

В ряду, построенном по арифметической прогрессии, разность значений двух соседних членов всегда постоянна во всем диапазоне ряда, т.е.

(2.1)

где Nn и Nn-1 – значения рядом стоящих членов ряда; d – разность (интервал) значений между двумя смежными членами ряда.

Пример арифметической прогрессии можно представить следующими рядами: 1÷2÷3÷5÷4÷5÷6÷7: 0,3÷0,6÷ 0,9÷1,2÷1,5...; 5÷50÷75÷100÷125÷150...

Недостатком такого ряда является его относительная неравномерность, т.е. нецелесообразная разреженность значений в зоне малых величин и сгущенность их в зоне больших величин (увеличение количества больших типоразмеров по сравнению с количеством малых типоразмеров).

Так, относительная разность между членами арифметического ряда 1, 2, 3,..., 10 для чисел 1 и 2 составляет 200%, а для чисел 9 и 10 всего 11%. Этот недостаток ограничивает возможности использования параметрических рядов на основе арифметической прогрессии.

Чаще применяются ступенчато-арифметические ряды, в которых разность (интервал) значений является постоянной не для всего ряда, а только для определенной его части. Для малых типоразмеров ряда разность выбирается меньшей, для больших – большей.

Любой член ряда в пределах данной группы может быть вычислен по формуле

(2.2)

где – первый член ряда; d – знаменатель прогрессии; п – номер искомого члена.

Так, в ГОСТе 8724-2002 (ИСО 261-98) "Основные нормы взаимозаменяемости. Резьба метрическая. Диаметры и шаги" (введен в действие постановлением Ростехрегулирования России от 23.06.2003 № 201-ст) представлены такие ряды стандартных резьб, как: 2–2, 5–3–3, 5–4–4, 5–5... – 145– 150–155–160–165... при разности 0,1-0,2-0,5-1-... –5...

Ряды предпочтительных чисел, построенные на основе геометрической прогрессии, являются более удобными.

Геометрическая прогрессия представляет собой ряд чисел с постоянным отношением двух смежных членов ряда, при этом каждый член ряда является произведением предыдущего члена и постоянной для данного ряда величины, которая называется знаменателем геометрической прогрессии.

Пример геометрической прогрессии:

1÷2÷4÷8÷16÷32...; 1÷1,1÷1,21÷1,331...; 10÷100÷1000÷10 000...

Знаменателями прогрессии соответственно являются 2; 1,1 и 10.

Каждый член прогрессии определяется по формуле

(2.3)

где i – порядковый номер члена; φ – знаменатель прогрессии.

При значении φ = 2 прогрессия имеет вид: ÷2÷4÷8÷ 16÷32...; при φ = 1,6: 1÷1,6÷2,5÷4÷6,3... При этом порядковым членом прогрессии для единицы является 0.

Геометрические прогрессии обладают важными свойствами, имеющими большое практическое значение.

Отношение двух смежных членов всегда постоянно и равно знаменателю прогрессии:

(2.4)

Произведение или частное каждых любых членов такой прогрессии всегда является ее членом:

(2.5)

Целая положительная или отрицательная степень любого числа такой прогрессии всегда является членом этой прогрессии:

(2.6)

Геометрическая прогрессия имеет свои недостатки.

Сумма и разность членов прогрессии в общем случае не являются членами прогрессии: 8-2 = 6; 4 – 1 = 3; 4 + 8=12 (имеются исключения 8 – 4 = 4; 16 – 8 = 8).

Члены геометрической прогрессии в десятичной системе не являются круглыми числами и для практического применения требуют округления. Исключение составляет геометрическая прогрессия со знаменателем 10 (...0,01 ÷ 0,1 ÷ 1 ÷ 10 ÷ 100 ÷ 1000...), но из-за большой относительной разности (900%) такая прогрессия на практике не применяется.

На основании перечисленных свойств геометрическая прогрессия, определяемая из произведений членов или их целых степеней, всегда будет подчиняться закономерности ряда.

Например, если ряд определяет линейные размеры, то площади и объемы, образованные из этих линейных величин, будут подчиняться его закономерности.

Наиболее удобными для целей стандартизации являются геометрические прогрессии, включающие число единица и имеющие знаменатель корень из 10:

(2.7)

В настоящее время установлены четыре основных ряда предпочтительных чисел (R5, R10, R20, R40) и дополнительный ряд R80, применение которого допускается в отдельных, только технически обоснованных случаях (табл. 2.1).

Число в условном обозначении ряда (R5, R10 и др.) представляет собой степень корня из 10 и показывает количество членов в пределах ряда. Количество чисел в десятичном интервале пятого ряда равно пяти; десятого – 10; двадцатого – 20 и т.п.

Предпочтительные числа и ряды, которых четыре, выглядят следующим образом:

R5 – 1,00; 1,60; 2,50; 4,00; 6,30; 10,00... имеет знаменатель прогрессии;

R10 – 1,00; 1,25; 1,60; 2,00; 2,50; 3,15; 4,00; 5,00; 6,30; 8,00; 10,00 имеет знаменатель прогрессии;

R20 – 1,00; 1,12; 1,25; 1,40; 1,60; 1,80; 2,00; 2,24; 2,36; 2,50; 2,80; 3,15; 3,55; 4,00; 4,50; 5,00; ... 10,00 имеет знаменатель прогрессии;

R40 – 1,00; 1,06; 1,12; 1,18; 1,25; 1,32; 1,40; 1,50; 1,60; 1,70; 1,80; 1,90; 2,00 ... 10, 00 имеет знаменатель прогрессии

R80 – 1,00; 1,03; 1,06; 1,09; 1,12; 1,15; 1,18; 1,22 ... 10,00 имеет знаменатель

Таблица 2.1

Предпочтительные числа и ряды

Условное обозначение ряда	Знаменатель прогрессии	Количество членов в пределах ряда
R5		5
R10		10
R20		20
R40		40
R80		80

Ряды предпочтительных чисел безграничны в обоих направлениях. Числа свыше 10 получаются умножением значений, установленных в интервале 1 ÷ 10 на 10; 100; 1000 и т.д., а числа менее единицы – на 0,1; 0,01; 0,001 и т.д.

При выборе того или иного ряда учитывают интересы не только потребителей продукции, но и изготовителей.

Частота параметрического ряда должна быть оптимальной: слишком "густой" ряд позволяет максимально удовлетворить нужды потребителей (предприятий, индивидуальных покупателей), но, с другой стороны, чрезмерно расширяется номенклатура продукции, распыляется производство, что приводит к большим производственным затратам. Поэтому ряд R5 является более предпочтительным по сравнению с рядом R10, а ряд R10 предпочтительнее ряда R20.

Система предпочтительных чисел дает возможность устанавливать наиболее рациональную закономерность построения параметрических рядов изделии и согласовывать основные взаимосвязанные параметры и размеры в различных областях деятельности.

Например, практика стандартизации в машиностроении показала, что параметрические ряды деталей и узлов машин должны базироваться на параметрических рядах машин и оборудования.

При этом целесообразно руководствоваться следующим правилом: ряду параметров машин по R5 должен соответствовать ряд размеров деталей по R10, ряду параметров машин R10 – ряд размеров деталей по R20 и т.д.

В соответствии с рядами параметрических чисел выбирают грузоподъемность транспортных средств, контейнеров, вместимость складов.

Так, в целях более эффективного использования тары для консервных банок и транспортных средств для их перевозки предлагается ряд грузоподъемности железнодорожных вагонов и автомашин и ряд размеров контейнеров, ящиков и отдельных консервных банок строить по ряду R5.

В радиотехнике уже давно применяются предпочтительные числа, построенные по рядам Е, принятые МЭК. Ряды Е состоят из округленных величин теоретических чисел со знаменателем для ряда ; для ряда ; для ряда . Например, ряды номинальных сопротивлений постоянных резисторов и ряды номинальной емкости постоянных конденсаторов выбираются по ряду Е6. Так, для конденсаторов ряд емкостей будет следующим: 1,5; 2,2; 3,3; 4,7; 6,8 (пф, мкф).