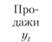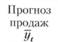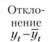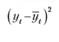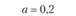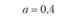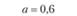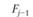Методы прогнозирования по временным рядам
Фактические продажи в определенный момент времени (yt) являются следствием наложения нескольких составляющих, а именно:
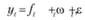 (5.3)
(5.3)
где 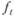 – долговременная составляющая (тренд), которая является непериодической компонентой, характеризующая общую (долговременную) тенденцию изменения продаж во времени;
– долговременная составляющая (тренд), которая является непериодической компонентой, характеризующая общую (долговременную) тенденцию изменения продаж во времени; 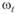 – сезонная составляющая, обусловленная периодической сменой времен года и, соответственно, погодных условий;
– сезонная составляющая, обусловленная периодической сменой времен года и, соответственно, погодных условий; 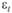 – случайная компонента (шум или высокочастотная составляющая), вызванная влиянием разного рода локальных факторов, не представляющих интереса для целей прогнозирования.
– случайная компонента (шум или высокочастотная составляющая), вызванная влиянием разного рода локальных факторов, не представляющих интереса для целей прогнозирования.
Приведенное уравнение называют еще аддитивной моделью прогноза, т.е. моделью, в которую факторы входят в виде алгебраической суммы, в отличие от мультипликативной модели, в которую факторы входят в виде произведения.
Кроме того, в статистике продаж могут присутствовать несистемные составляющие, появление которых вызвано сменой этапов жизненного цикла товара или проведением маркетинговых (рекламных) мероприятий по стимулированию спроса, однако их формализация представляет более длительный и сложный процесс.
1. Тренд продаж характеризует общую долгосрочную тенденцию в изменениях показателей потребительского спроса, на основании которой можно судить о динамике бизнеса компании в длительной перспективе. Например, восходящий тренд может свидетельствовать о стабильном росте продаж компании от года к году, несмотря на периодические сезонные спады, напротив, нисходящий тренд – признак устойчивого замедления деловой активности, что должно натолкнуть руководство на принятие соответствующих мер на стратегическом уровне. Наличие тренда свидетельствует о нестационарности функций, которые описывают динамику продаж во времени, поскольку их вероятностные характеристики подвержены сильной изменчивости.
Для относительно коротких временных рядов (до года) тренды аппроксимируются линейными уравнениями (первого порядка):
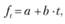 (5.4)
(5.4)
где t – момент времени, соответствующий рассчитываемому значению линии тренда; а и b – коэффициенты, которые в геометрическом смысле интерпретируются следующим образом: а – расстояние от начала координат до точки пересечения линии тренда с осью OY:
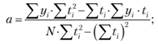 (5.5)
(5.5)
b – тангенс угла наклона линии тренда к оси ОХ:
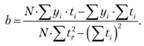 (5.6)
(5.6)
В более длительных рядах динамики продаж тренды могут иметь параболическую, экспоненциальную, логарифмическую, гиперболическую и прочие формы. Прикладные пакеты программных средств, такие как "Microsoft Exel", "MathCAD", позволяют автоматизировать процесс расчета коэффициентов уравнения тренда и тем самым облегчить работу аналитиков.
С помощью экстраполяции трендов можно прогнозировать общие долговременные тенденции в изменениях продаж товаров (услуг).
Пример
В табл. 5.2 приведены квартальные значения продаж товара оптовой компании. Для определения долговременной тенденции временного ряда воспользуемся формулами (5.4)-(5.6), после чего получим:
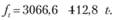
Для расчета линии тренда поочередно подставляем в уравнение вместо (t) порядковый номер каждого квартала, в том числе на прогнозируемый период.
Таблица 5.2
Статистика продаж товаров за 2011–2013 гг. и прогноз общей тенденции на 2014 г., тыс. руб.
|
Год |
№ квартала |
№ п/п |
Продажи yt |
Тренд ft |
|
2011 |
I |
1 |
3248 |
3179 |
|
II |
2 |
4326 |
3292 |
|
|
III |
3 |
2015 |
3405 |
|
|
IV |
4 |
3657 |
3518 |
|
|
2012 |
I |
5 |
3694 |
3631 |
|
11 |
6 |
4812 |
3743 |
|
|
III |
7 |
2215 |
3856 |
|
|
IV |
8 |
3819 |
3969 |
|
|
2013 |
I |
9 |
4115 |
4082 |
|
II |
10 |
6002 |
4195 |
|
|
III |
11 |
2849 |
4307 |
|
|
IV |
12 |
4846 |
4420 |
|
|
2014 (прогноз) |
I |
13 |
- |
4533 |
|
II |
14 |
- |
4646 |
|
|
III |
15 |
- |
4759 |
|
|
IV |
16 |
- |
4871 |
Нанесем полученные результаты на график и экстраполируем тренд на прогнозируемый период 2014 г. (рис. 5.3). Из приведенных расчетов видно, что продажи товара в компании имеют устойчивую тенденцию к росту (восходящий тренд). При этом коэффициент (b = 112,8) означает, что продажи компании в среднем увеличиваются в долгосрочной перспективе на 112,8 тыс. руб. в год.
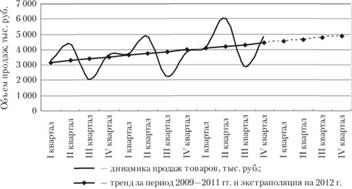
Рис. 5.3. Динамика продаж товаров оптовой компании и тренд
2. Сезонная составляющая (волна) обусловлена периодической сменой времен года (сезонов), что вызывает изменение предпочтений покупателей в отношении некоторых товаров (например, одежды и обуви, систем отопления и кондиционирования). Кроме того, урожай большинства сельскохозяйственных товаров стимулирует падение цен на рынке в летний период и, соответственно, вызывает рост их потребления. Некоторые товары могут иметь по одному сезонному всплеску и одному спаду продаж, некоторые – по два (так называемые демисезонные товары).
Для определения влияния сезонности в статистике продаж компании используются специальные показатели – индексы сезонности (Is), совокупность которых представляет сезонную волну. Индексы сезонности характеризуют долю объема продаж товара относительно его среднемесячного (среднеквартального) объема продаж за год.
Для ряда внутригодовой динамики, в котором основная тенденция роста (тренд) незначительна (или она не наблюдается совсем), изучение сезонности основано на методе постоянной средней, являющейся средней из всех рассматриваемых уровней. Обычно для каждого года рассчитывается средний уровень, а затем с ним сопоставляется уровень каждого анализируемого месяца (квартала):
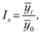 (5.7)
(5.7)
где 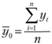 – среднее значение продаж за весь анализируемый период;
– среднее значение продаж за весь анализируемый период; 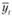 – среднее значение продаж в отдельно рассматриваемом месяце (квартале).
– среднее значение продаж в отдельно рассматриваемом месяце (квартале).
При наличии устойчивой тенденции в динамике продаж индексы сезонности определяются по формуле, позволяющей исключить влияние тренда:
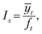 (5.8)
(5.8)
где 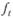 – значение тренда соответствующего периода времени.
– значение тренда соответствующего периода времени.
Пример
Рассчитаем для условий предыдущего примера индексы сезонности с учетом наличия долговременной тенденции к росту продаж (табл. 5.3) и нанесем полученные результаты на график (рис. 5.4).
Таблица 5.3
Статистика продаж товаров за 2011–2013 гг. и прогноз на 2014 г. с учетом общей тенденции и сезонной волны, тыс. руб.
|
Год |
№ квартала |
№ п/п |
Продажи yt |
Тренд ft |
Сезонная волна yt – ft |
Индекс сезонности Is |
|
2011 |
I |
1 |
3248 |
3179 |
69 |
1,02 |
|
II |
2 |
4326 |
3292 |
1034 |
1,31 |
|
|
III |
3 |
2015 |
3405 |
-1390 |
0,59 |
|
|
IV |
4 |
3657 |
3518 |
139 |
1,04 |
|
|
2012 |
I |
5 |
3694 |
3631 |
63 |
1,02 |
|
II |
6 |
4812 |
3743 |
1069 |
1,29 |
|
|
III |
7 |
2215 |
3856 |
-1641 |
0,57 |
|
|
IV |
8 |
3819 |
3969 |
-150 |
0,96 |
|
|
2013 |
I |
9 |
4115 |
4082 |
33 |
1,01 |
|
II |
10 |
6002 |
4195 |
1807 |
1,43 |
|
|
III |
11 |
2849 |
4307 |
-1458 |
0,66 |
|
|
IV |
12 |
4846 |
4420 |
426 |
1,10 |
|
|
2014 (прогноз) |
I |
13 |
4604 |
4533 |
- |
1,02 |
|
II |
14 |
6241 |
4646 |
- |
1,34 |
|
|
III |
15 |
2899 |
4759 |
- |
0,61 |
|
|
IV |
16 |
5031 |
4871 |
- |
1,03 |
В таблице прогнозные значения продаж получены с помощью экстраполяции тренда, скорректированного на сезонность, в соответствии с рассчитанными индексами, например, для I квартала 2014 г.:
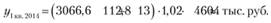
При этом для целей прогноза на 2014 г. использовались индексы сезонности, усредненные за три прошедших года, например для II квартала:
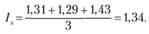
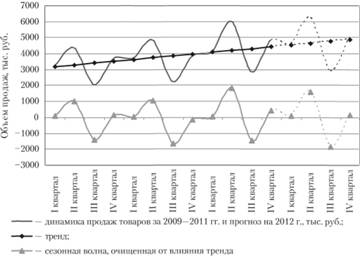
Рис. 5.4. Прогноз продаж оптовой компании с учетом долговременной тенденции и сезонности
Полученные результаты свидетельствуют, что наибольшая потребность в товарах наблюдается во II квартале, а наибольший спад – в III, что может позволить разработать методику более эффективного использования денежных средств для обеспечения компании необходимыми запасами.
Стоит заметить, что сезонные колебания продаж, а также изменения спроса, вызванные сменой этапов жизненного цикла товара, представляют собой периодические (или квазипериодические) процессы, которые тоже можно описывать с помощью гармонического анализа, когда значения временного ряда представляются в виде слагаемых ряда Фурье (гармоник), которые имеют соответствующие амплитуды и фазы.
3. Случайная компонента (шум) появляется в результате действия относительно слабых или второстепенных факторов, предсказать которую можно только с некоторой вероятностью. Среди примеров появления случайной компоненты можно привести такие, как отсутствие продаж вследствие дефицита запасов или остановка деятельности предприятия органами государственного надзора и т.д.
Учесть возможное влияние случайной компоненты можно через расчет ошибки прогноза по формуле среднеквадратического отклонения:
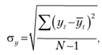 (5.9)
(5.9)
где 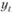 – фактические продажи в определенный момент времени;
– фактические продажи в определенный момент времени; 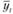 – прогнозные значения продаж в соответствующий фактическим продажам момент времени.
– прогнозные значения продаж в соответствующий фактическим продажам момент времени.
Пример
Определим ошибку прогноза для условий предыдущего примера (табл. 5.4 и рис. 5.5).
Таблица 5.4
Оценка ошибки прогноза за 2014 г., тыс. руб.
|
Год |
№ квартала |
№ п/п |
|
|
|
|
|
2011 |
I |
1 |
3248 |
3229 |
19 |
346 |
|
II |
2 |
4320 |
4423 |
-97 |
9394 |
|
|
III |
3 |
2015 |
2074 |
-59 |
3519 |
|
|
IV |
4 |
3657 |
3633 |
24 |
584 |
|
|
2012 |
I |
5 |
3694 |
3688 |
6 |
40 |
|
II |
6 |
4812 |
5029 |
-217 |
47 128 |
|
|
III |
7 |
2215 |
2349 |
-134 |
18 008 |
|
|
IV |
8 |
3819 |
4099 |
-280 |
78 286 |
|
|
2013 |
I |
9 |
4115 |
4146 |
-31 |
960 |
|
II |
10 |
6 02 |
5635 |
367 |
134 501 |
|
|
III |
11 |
2 49 |
2624 |
225 |
50 597 |
|
|
IV |
12 |
4 46 |
4565 |
281 |
79 100 |
|
|
2014 (про гноз) |
I |
13 |
- |
4604 |
Итого: 422 462 |
|
|
II |
14 |
- |
6241 |
|||
|
III |
15 |
- |
2899 |
|||
|
IV |
16 |
- |
5031 |
|||
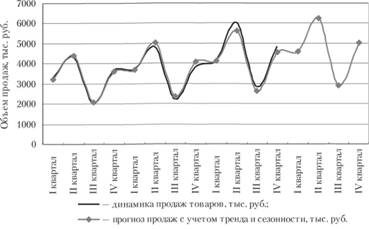
Рис. 5.5. Фактические и прогнозируемые продажи оптовой компании с учетом долговременной тенденции и сезонности
Подставив полученную сумму квадратов отклонений фактических продаж от прогнозируемых, получим:
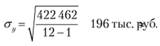
Таким образом, в 68% случаев продажи товаров будут находиться в интервале ± 196 тыс. руб. относительно прогнозируемого значения[1]. Например, для I квартала 2014 г.: (4604 ± 196) тыс. руб. Для целей формирования запаса нас интересует только верхняя граница интервала: 4604 + 196 = 4800 тыс. руб.
Случайная компонента достаточно сложно поддается формализации, и поэтому большинство методов исследования временных рядов предполагают различные способы ее фильтрации, позволяющие увидеть регулярные составляющие более четко. Одним из наиболее распространенных способов устранения случайных колебаний продаж являются различные методы сглаживания, позволяющие при относительно стабильном спросе прогнозировать потребность в запасах, экстраполируя полученные кривые в область будущих периодов.
Метод простого скользящего среднего производится по формуле среднего арифметического для относительно коротких временных интервалов:
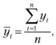 (5.10)
(5.10)
где уt – значение продаж в период времени t; t – индекс периода времени; п – число временных периодов.
При этом число периодов осреднения принимается равным количеству периодов между соседними никами или впадинами на графике, при котором колебания лучше всего сглаживаются.
Пример
Предприятие, специализирующееся в области автоперевозок, планирует потребность в дизельном топливе исходя из статистики фактического расхода по прошлым периодам (табл. 5.5).
Таблица 5.5.
Расчет потребности в дизельном топливе методом простого скользящего среднего
|
Месяц/год |
Фактический расход, л/мес. |
Число рабочих дней в месяце |
Средний расход, л/день |
Прогноз среднего расхода, л/день |
Прогноз среднего расхода, л/мес. |
Прогноз среднего расхода, л/день |
Прогноз среднего расхода, л/мес. |
|
Интервал расчета скользящей средней |
|||||||
|
2 мес. |
3 мес. |
||||||
|
Январь 10 |
1159 |
15 |
77 |
- |
- |
- |
- |
|
Февраль 10 |
1566 |
19 |
82 |
- |
- |
- |
- |
|
Март 10 |
924 |
22 |
42 |
80 |
1756 |
- |
- |
|
Апрель 10 |
1081 |
22 |
49 |
62 |
1369 |
67 |
1479 |
|
Май 10 |
2333 |
19 |
123 |
46 |
866 |
58 |
1099 |
|
Июнь 10 |
1 096 |
21 |
52 |
86 |
1 805 |
71 |
1497 |
|
Июль 10 |
2004 |
22 |
91 |
88 |
1925 |
75 |
1644 |
|
Август 10 |
2474 |
22 |
112 |
72 |
1576 |
89 |
1952 |
|
Сентябрь 10 |
3226 |
22 |
147 |
102 |
2239 |
85 |
1876 |
|
Октябрь 10 |
1268 |
21 |
60 |
130 |
2721 |
117 |
2452 |
|
Ноябрь 10 |
1347 |
21 |
64 |
104 |
2174 |
107 |
2237 |
|
Декабрь 10 |
2255 |
22 |
103 |
62 |
1370 |
90 |
1989 |
|
Январь 11 |
1300 |
16 |
81 |
83 |
1333 |
76 |
1211 |
|
Февраль 11 |
1770 |
19 |
93 |
92 |
1746 |
83 |
1570 |
|
Март 11 |
3163 |
23 |
138 |
87 |
2005 |
92 |
2123 |
|
Апрель 11 |
1378 |
21 |
66 |
115 |
2422 |
104 |
2183 |
|
Май 11 |
3758 |
19 |
198 |
102 |
1930 |
99 |
1877 |
|
Июнь 11 |
3195 |
20 |
160 |
132 |
2634 |
134 |
2673 |
|
Июль 11 |
4040 |
21 |
192 |
179 |
3754 |
141 |
2962 |
|
Август 11 |
- |
23 |
- |
176 |
4049 |
183 |
4216 |
Прогнозные значения расхода дизельного топлива получены следующим образом:
– для марта 2010 г. при интервате расчета скользящей средней 2 мсс.:

– для апреля 2010 г. при интервале расчета скользящей средней 3 мес.:
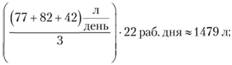
и т.д.
Графическая иллюстрация произведенных расчетов представлена на рис. 5.6.
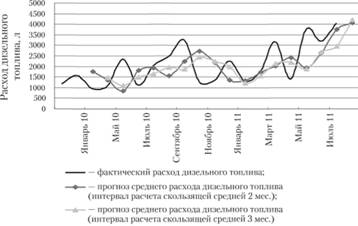
Рис. 5.6. Фактические и прогнозные значения расхода дизельного топлива за период январь 2010 – август 2011 г.
Необходимо заметить, что не стоит осреднять по большому количеству периодов, чтобы не допустить снижения чувствительности скользящей средней к изменениям спроса.
Для экономических дисциплин, к которым, несомненно, относится и логистика, значения статистического ряда, отстоящие от настоящего момента на разные периоды времени, не может использоваться для целей прогнозирования с одинаковым весом. Например, предприятие, имеющее десятилетнюю историю продаж, начинало свою деятельность с одного розничного магазина на окраине Москвы, сегодня же оно имеет представительства почти во всех федеральных округах России. Очевидно, что статистика потребительского спроса десятилетней давности представляет меньший интерес, чем значения ближайшего к сегодняшнему моменту времени периода. Поэтому для учета значимости отдельных временных периодов можно воспользоваться методом взвешенной скользящей средней:
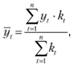 (5.11)
(5.11)
где 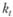 – коэффициент значимости периода времени.
– коэффициент значимости периода времени.
Для учета значения предыдущего прогноза и его отклонения от фактического значения используется метод экспоненциального сглаживания:
 (5.12)
(5.12)
где 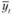 – прогнозируемый объем потребности в следующем периоде времени t;
– прогнозируемый объем потребности в следующем периоде времени t; 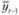 – прогнозируемый объем потребности в предыдущем периоде времени (/: – 1);
– прогнозируемый объем потребности в предыдущем периоде времени (/: – 1); 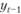 – фактическая потребность в предыдущем периоде времени (t – 1); (ί – 2) – индекс периода времени, предшествующего предыдущему; а – константа сглаживания.
– фактическая потребность в предыдущем периоде времени (t – 1); (ί – 2) – индекс периода времени, предшествующего предыдущему; а – константа сглаживания.
Последний параметр подбирается эмпирическим путем, в том числе по результатам анализа точности (ошибок) прогноза за прошлые периоды. Необходимо определить такое значение (а), чтобы, с одной стороны, прогноз был чувствителен к изменениям временного ряда, а с другой – хорошо сглаживал скачки потребительского спроса, обусловленные случайными факторами.
Название метода связано с тем, что более ранним значениям статистики продаж даются веса, уменьшающиеся по экспоненциальному закону (табл. 5.6).
Таблица 5.6
Значения весов для значений продаж, относящихся к разным периодам времени
|
Вес данных |
|
|
|
|
|
0,2 |
0,4 |
0,6 |
|
|
0,16 |
0,24 |
0,24 |
|
|
0,128 |
0,144 |
0,096 |