Методы проекции градиента на линейные многообразия
Рассмотрим решение задачи квадратичного программирования: вычислить

используя проектирование текущих решений на линейные многообразия, определяемые ограничениями задачи.
Известно, что точка г* = Рш(г) называется проекцией точки на множество ЗЭ, если Рв(2) удовлетворяет условию
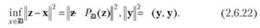
Рассмотрим аналитическое представление операторов проектирования точки на линейное многообразие
© = {х|Ах Ь, А= тх",Ъ е9(ш} еДопА'й'им, что множество © не пусто, т.е. система ограничений Ах = Ь имеет решение. Для этого в соответствии с теоремой Кронекера — Капелли необходимо и достаточно, чтобы ранг матрицы А был равен рангу расширенной матрицы (А I Ь). Пусть необходимо найти проекцию точки Ъ на В. В соответствии с определением (2.6.22) необходимо найти Рв(г), доставляющий мини-
мум р-х|| =ра(г) г|р при ограничениях Ах = Ь. Другими словами, надо решить задачу: вычислить

Поскольку данная задача укладывается в рамки обычной "лагранжевой" схемы, известной из математического анализа, то составим функцию Лагранжа:
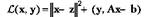
и выпишем известные необходимые условия Лагранжа:

Тогда из первого условия имеем х„(у) = г Агу/2, откуда определяется выражение для у* через Ъ с учетом того, что Ах,(у) = Ь:у, 2(ААГ)-|А-2(ААГ)-,Ь.
Из последнего равенства с учетом условия х„(у) = г А' у / 2 оператор проецирования (проектор) вектора Ъ на множество ЗВ:

Таким образом, соотношение (2.6.23) устанавливает вид оператора проецирования на линейное многообразие. Если Ь = От, то линейное многообразие преобразуется в линейное подпространство (содержит нулевой вектор), а оператор проецирования на линейное подпространство задается матрицей вида

Полученные представления операторов проецирования позволяют перейти к формулировке вычислительной схемы метода:

где направление рк строится с помощью проекции градиента функционала на линейное многообразие. Алгоритм решения задачи (2.6.21), согласованный с методом сопряженных градиентов (см. подпараграф 2.5.3), имеет следующий вид.
Шаг 1. Вычисляется вектор х0, удовлетворяющий ограничениям задачи, полагаем х = х0.
Шаг 2. Вычисляется вектор />,-"= (Е 1ф) '(х*), где Р[ = А'''(АА''')"'А, причем матрица А имеет строки, определенные в (1). Полагаем к=.
Шаг 3. Вычисляется новое приближение:

где шаг определяется равенством ам =-(ф'(х/,), рА+))/ /(Р*+1-Оры).
Шаг 4. Определяется новое направление в соответствии с равенством:

Шаг 5. Полагается хА = к 1,рм р^+1.
Шаг 6. Если & = ", то — переход к шагу 7, иначе — к шагу 3.
Шаг 7. Останов.
Рассмотренный алгоритм предназначен для частной задачи квадратичного программирования.
Общий метод проекции градиента для общей задачи квадратичного программирования на основе теоремы Куна — Таккера
Общая задача квадратичного программирования формулируется в следующем виде: вычислить

Идея решения этой общей задачи состоит в организации итеративного процесса:

где направление р,, вычисляется исходя из проектирования градиента на многообразие (линейное), образованное активными ограничениями. Проверка оптимальности выполняется по теореме Куна — Таккера.
Определение. Ограничения задачи (2.6.24), выполняемые как равенства в точке очередного приближения, называются активными ограничениями.
Другими словами, идея метода состоит в последовательном решении семейства простейших задач квадратичного программирования типа (2.6.21) па множествах сменяющих друг друга линейных многообразий с проверкой оптимальности на основе дифференциальных условий теоремы Куна — Таккера.
Определение общей идеи алгоритма позволяет сформулировать алгоритм метода.
Шаг 1. Вычисляем точку х0, используя какие-либо методы решения линейных неравенств и равенств.
Шаг 1а. Строим индексное множество /0, состоящее из номеров активных ограничений (выполняющихся в точке х0 как равенства): 70=7(х) Ф'|(а;,х0) О?/ JQJ<>}. Другими словами, ./о — множество номеров активных ограничений.
Шаг 16. Если Уо*^- то переходим к шагу 2, иначе -положим Р, = О и перейдем к шагу 4.
Шаг 2. Вычислим матрицу \,, и вектор ТЛ: У0 = (Ауо)Ауи, и<г= '(хо)- Строки матрицы Ауо есть векторы а;, соответствующие уравнениям и неравенствам, выполняющимся в точке х() как равенства.
Шаг 3. Вычисляется оператор Р, = А^АУ,, А^А^А^ )_| А7(|.
Шаг 4. Определяется направление движения на данном шаге: р0- (-Е 1$) '(х0).
Шаг 5а. Если (Е-Р,)ф'(хо)*0, то, положив к = О, переходим к шаг)' 66, иначе — к шагу 56.
Шаг 56. Если (Е-Р,)ф'(хо) = 0 и все компоненты вектора и > 0, то х0 — решение задачи и необходимо перейти к шагу 7, иначе — к шагу 6а.
Шаг 6а. Формируется новое индексное множество /*, полученное из JQ путем исключения г, для которых {/; < О, и если 7**0, то вычисляется оператор Р=А^,(А^,А^,)_1А^".
Положив /г = 0, переходим к шагу 66, иначе — (если /° ф 0) переходим к шагу 16.
Шаг 6б. Вычисляется р(— (Е 1ф) '(хо) (см. шаг 4).
Шаг 6е. Вычисляются

Шаг 6г. Если а < т, то переход к шагу 6д, иначе — к шагу 6з.
Шаг 63. Вычисление Х/,+| = - а/грк+].
Шаг бе. Полагаем & = & + 1 и вычисляем вектор нового направления

Шаг 6ж. Если рА+1 * 0 (или £ < и), то переход к шагу 6", иначе (когда рк+1 = 0 или к = п) — полагается х0 = х^, и происходит переход к шагу 16.
Шаг 6з. Вычисляется х^+1 = хА - трА+1. Полагается х0 = хА+1, и — переход к шагу 16.
Шаг 7. Останов.
Как следует из схемы алгоритма, минимизация на подпространстве осуществляется с помощью объединения проекции градиента и метода сопряженных градиентов. Проиллюстрируем процедуру минимизации.
Пример
Найдем решение следующей задачи: вычислить
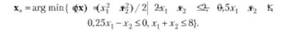
Решение. Сформулируем задачу в стандартной форме: вычислить

Шаг 1а. Вычисляется допустимое решение х0 = (4,3)7", используя метод решения системы линейных равенств и неравенств.
Шаг 1 б. Формируется индексное множество ,/„ = (2).
Шаг 1в. Множество /„ *0, поэтому — переход к шагу 2. Шаг 2. Вычисляется матрица У0 и вектор V:

Шаг 3. Формируется оператор

Шаг4. Вычисляется вектор направления

Шаг 5а. Если вектор р0 ф О, то, положив к = О, происходит переход к шагу 6а, иначе — к шагу 56.
Шаг56. Если векторр0 = 0и все компоненты вектора и > 0, то х0 — решение задачи и необходимо перейти к шагу 7, иначе — к шагу 6а.
Шаг 6а. Вычисляется вектор
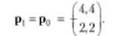
Шаг 6б. Вычисляются а и т:

Шаг 6в. Если а > т, то переход к шагу 6г. Шаг 6г. Вычисляется

Полагается хн = х^н - (2, 2)т, и выполняется переход к шагу 16. Начинается новая большая итерация метода. Шаг 16. Строится индексное множество J^) = {1(. (Элемент г = 2 исключается из у0, проверьте это самостоятельно.)
Шаг 1в. Поскольку J^i * 0. то переход к шагу 2. Шаг 2. Вычисляются матрица У0 и вектор и:

Шаг 3. Вычисляется оператор

Шаг 4. Определяется вектор р0 = -(1,2, 2,4) г. Шаг 5а. Поскольку р0 * 0, то происходит переход к шагу 66, положив ¿=0.
Шаг 6б. Вычисляется р, =р0 = -(1,2,2,4)7". Шаг 6е. Вычисляются а и т:

Шаг 6г. Если а > т, то переход к шагу 6з, иначе — к шагу 7. Шаг 6з. Вычисляется вектор

Шаг 7. Полагается = х^, (, и происходит переход к шагу 16. Новая большая итерация метода.
Шаг 1б. Строится индексное множество У0, которое для данного
вектора х„ - -(1,14,0,28)г имеет вид ]0 = {1,3}.
Шаг 1в. Поскольку J0 *■ 0, то — переход к шагу 2. Шаг 2. Вычисляются векторы У„ и и:

Шаг 3. Вычисляется оператор

Шаг 4. Определяется вектор р0 = (0,0)'.
Шаг 5а. Поскольку (Е-Р,)ф'(хо) = (0.0)г и все компоненты вектора и > 0, то х,, — решение задачи, далее происходит переход к шаг)' 7.
Шаг 7. Останов.
Можно построить допустимую область, определяемую системой неравенств, рассматриваемых в данной задаче. Пусть х0 = (х0, хо)т= (4, 3)г — исходная допустимая точка (находится путем решения неравенств), а точка х, = (2, 2)т получена после первой большой итерации метода. Активное многообразие соответствует двум неравенствам, выполняющимся как равенства. Точка х, = (1,14,0,28)'"— оптимальное решение.
Характерно, что геометрически условия оптимальности означают возможность представления вектора антиградиента функционала в виде положительной линейной комбинации векторов нормалей активных ограничений. Такой вывод следует из условия (Е-Р,)ф'(х0) = 0, преобразуя которое можно получить (при А = Ауо):

Таким образом, метод проекции градиента использует утверждения теоремы Куна — Таккера для контроля выполнения условий оптимальности на каждой итерации метода, формирует семейство активных многообразий, на которых решаются задачи условной минимизации.
Метод позволяет получить точное решение за конечное число итераций, а также может быть основой решения более сложных выпуклых задач минимизации функционалов при условии нелинейных ограничений.