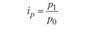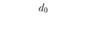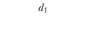Методы построения индексов. Агрегатная форма индекса и индексы, средние из индивидуальных

Назначение индексов – изучение динамики сложных явлений, которые состоят из относительно более простых отдельных элементов. Изменение отдельных элементов характеризуется с помощью индивидуальных индексов, а сложных явлений в целом – на основе общих индексов.

Методы построения индивидуальных индексов различных явлений в целом одинаковы. Например, требуется проанализировать показатели коммерческой деятельности торгового предприятия, занимающегося реализацией бытовой техники. Допустим, имеется информация за два смежных месяца его деятельности об объеме реализации конкретных видов бытовой техники (физический объем продаж – q), розничных ценах единицы товара (р), товарообороте (стоимости реализации – ).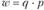

Динамика признаков по отдельным элементам (товарам) изучаемой совокупности за сравниваемые периоды может быть оценена на основе индивидуальных индексов, представляющих соотношение этих признаков за февраль ("1") и январь ("0"):

Так как w = q • р, то справедливо будет равенство 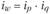(система индивидуальных индексов).

Поскольку индивидуальный индекс получается путем сравнения двух величин, при его расчете следует выполнять требования сопоставимости этих величин, такие как одинаковая методология исчисления, однокачественность сравниваемых величин, одна и та же территория и т.д.

Для расчета индексов тех же признаков по всей совокупности товаров торгового предприятия используют общие (сводные) индексы. Совокупность таких товаров (например, телефонов, холодильников, телевизоров, утюгов и т.д.) состоит из разных потребительских стоимостей, непосредственно несоизмеримых. Следовательно, чтобы рассчитать индексы цен и физического объема реализации, необходимо несоизмеряемые составные элементы совокупности выразить их общей мерой – стоимостью. Для этой цели используют агрегатную форму сводного аналитического индекса, которая является основной в системе экономических индексов.

Агрегатная форма индекса наряду с индексируемым признаком (динамика которого изучается) содержит признак – вес, который и позволяет соизмерить разнородные элементы совокупности. Его значение в агрегатном индексе должно быть неизменным, чтобы не искажать оценку изменения индексируемого признака. Однако возникает вопрос: за какой период (базисный или текущий) необходимо включать в расчет индекса признак – вес?

В международной статистической практике в настоящее время наиболее широко применяют формулы индексов Ласпейреса, Пааше и Фишера, которые названы по именам ученых, предложивших их в процессе развития теории индексов цен^[1].

В российской статистике в зависимости от целей исследования и информационного обеспечения применяют методику построения агрегатных индексов либо Пааше (с текущими весами), либо Ласпейреса (с базисными весами):

а) методика Э. Ласпейреса (1871):

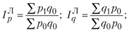
б) методика Г. Пааше (1874):

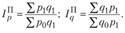
Обе методики построения агрегатных индексов обеспечивают сопоставимость оценок изменений факторов. Однако при этом не обеспечивается увязка индексов в систему, т.е. 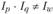. Вместе с тем увязка индексов физического объема, цен и стоимости является одним из основных требований теории индексов, разработанной американским статистиком И. Фишером (1927). Указанное неравенство индексов свидетельствует, что они не удовлетворяют условию (тесту) обратимости по факторам ("факторной пробы"), а следовательно, считаются неправильно построенными. Согласно этой теории правильно построенные индексы должны отвечать и другим требованиям – тестам обратимости во времени и кружного испытания.

Однако в системе национальных счетов допускается использование на практике как индекса Ласпейреса, так и индекса Пааше при решении аналитических и технических задач.

Взаимосвязанные агрегатные индексы увязываются в систему техническим способом с использованием в этих индексах весов разных периодов:

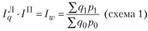
или

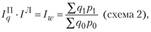
где 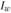– простой сводный индекс стоимости (товарооборота).

Рассмотрим обе схемы увязки агрегатных индексов в систему на условном примере реализации бытовой техники торговым предприятием за два смежных месяца года (табл. 7.1).

Таблица 7.1

Реализация некоторых видов бытовой техники торговым предприятием за январь и февраль

Товары	Количество проданных единиц		Цена за единицу, тыс. руб.		Стоимость товарооборота, тыс. руб.		Условный товарооборот
	январь	февраль	январь	февраль	январь	февраль	январь	февраль
Холодильники	30	28	12	12,5	360	350	336	375
Телевизоры	120	150	4,8	4,5	576	675	720	540
Компьютеры	25	32	30	31	750	992	960	775
Мобильные телефоны	240	280	2,6	1,9	624	532	728	456
Итого	X	X	X	X	2310	2549	2744	2146

Индекс товарооборота за указанный период

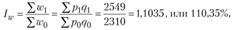
т.е. в феврале по сравнению с январем объем реализации торгового предприятия увеличился на 10,35%, или на 239 тыс. руб. (разность между числителем и знаменателем индекса).

Для определения влияния отдельных факторов на формирование индекса товарооборота рассчитаем агрегатные индексы физического объема реализации (Iq) и цен (Iр) с текущими и базисными весами соответственно:

Система индексов по схемам 1 и 2 выглядит следующим образом:

Таким образом, на основе этой системы индексов можно сделать вывод, что прирост товарооборота стал следствием увеличения объема продаж за счет роста спроса на бытовую технику при одновременном среднем снижении цен на нее.

Агрегатные индексы цен и физического объема с разными весами показывают различные результаты изменения индексируемых признаков (в нашем примере эти различия незначительны). Как правило, индекс с базисными весами больше, чем с текущими. Такое соотношение двух индексов получило в экономической литературе название эффекта Гершенкропа, по имени американского ученого, занимавшегося теорией индексов в 1930-х гг. Особенно интересно, что этот эффект проявляется при сравнениях за длительный период времени, а также при наличии обратной пропорциональной зависимости между физическим объемом продукции и ценами.

Более заметные различия в результатах индексов Пааше и Ласпейреса в нашем примере обнаруживаются, если указанные индексы выразить в разностной форме. Разность числителя и знаменателя соответствующего индекса характеризует абсолютный прирост (уменьшение) стоимости товарооборота за счет:

а) изменения физического объема реализации:

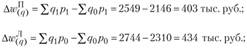
б) изменения цен:

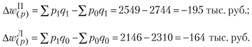
Отсюда абсолютный прирост товарооборота в размере 239 тыс. руб. можно представить следующим образом:

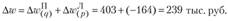
или

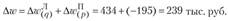
На основе абсолютных значений влияния каждого из факторов на общее изменение товарооборота можно определить их вклад в формирование общего результативного индекса:

• по приросту (снижению) товарооборота за счет изменения физического объема реализации:

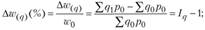
• приросту (снижению) товарооборота за счет изменения цен:

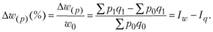
Отсюда совокупное влияние в относительном выражении имеет вид

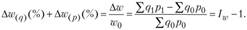
В нашем примере такой расчет согласно схеме 1 выглядит следующим образом:

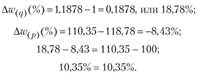
Если агрегатные индексы факторных признаков влияют на результативный индекс однонаправленно, можно оценить долю отдельных факторов в формировании результата:

а) доля прироста (снижения) товарооборота за счет изменения физического объема реализации

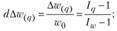
б) доля прироста (снижения) товарооборота за счет изменения цен

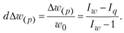
Сумма этих факторов должна быть равна 1 или 100% (если доли выражены в %).

Рассмотренные выше агрегатные индексы в виде мультипликативной модели (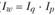) могут быть построены только для со

поставимого круга элементов анализируемых совокупностей сложных явлений в базисном и отчетном периодах.

Практически при использовании индексного метода анализа исследователю приходится сталкиваться с наличием в изучаемой совокупности несопоставимых элементов. Это может быть связано, например, с появлением на рынке новых или существенно улучшенных товаров в отчетном периоде в связи с их производством или импортом.

Вместе с тем традиционные агрегатные индексы как с текущими, так и с базисными весами либо непосредственно не учитывают несопоставимые элементы совокупности (формула Ласпейреса), либо при их расчете появляется проблема оценки признаков новых товаров (например, индекса цен), которых не было в базисном периоде (формула Пааше).

Индексный метод анализа показателей различных явлений требует учитывать данные по полному кругу элементов: сопоставимых и несопоставимых. Для решения этой задачи в статистике разработаны специальные приемы построения индексов для обобщенных данных по группам товаров, видам продукции, предприятиям, рынкам. Эти методы достаточно подробно изложены в современных учебниках по общей теории статистики, поэтому в настоящем учебнике они не рассматриваются.

Наряду с агрегатной формой общие индексы могут быть построены как средние из индивидуальных индексов, тождественные агрегатным. Обычно применение того или иного способа расчета общих индексов определяется не только задачами исследования, но и характером исходной информации об изучаемых явлениях. Например, в сфере розничной торговли легче получить сведения не о количестве проданных товаров, а об их стоимости. Кроме того, расчет индивидуальных индексов технически прост, что в ряде случаев значительно снижает трудоемкость вычислений общих индексов в форме средних. Немаловажно, что при использовании индивидуальных индексов имеется возможность наглядно представить динамику изучаемого явления по отдельным элементам совокупности и их роль в формировании общего индекса. В связи с этим в отечественной и зарубежной статистике индексы в виде средних из индивидуальных и их различные модификации получили широкое применение^[2].

Например, индекс цен с текущими весами может быть представлен в виде средней гармонической взвешенной из индивидуальных:

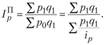
Индекс цен с базисными весами можно выразить в виде средней арифметической взвешенной из индивидуальных:

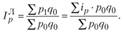
Данные формулы можно значительно упростить, рассчитав доли товарооборота отдельных видов продукции в его общем объеме для отчетного и базисного периодов:

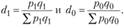
Тогда формулы индексов ден приобретают следующий вид:

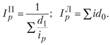
Рассчитаем на основе данных, приведенных в табл. 7.1, указанные индексы ден в виде средних из индивидуальных, предварительно вычислив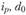 и (табл. 7.2).

Таблица 7.2

Расчетные значения индивидуальных индексов цен и долей товарооборота по некоторым видам бытовой техники

Товары
Холодильники	1,042	0,156	0,137
Телевизоры	0,937	0,249	0,265
Компьютеры	1,033	0,325	0,389
Мобильные телефоны	0,731	0,270	0,209
Итого	X	1,00	1,00

Рассчитываем сводные индексы ден:

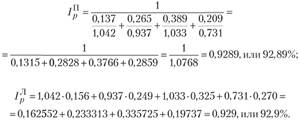
Мы получили те же значения индексов, что и в агрегатной форме. При этом индивидуальные индексы позволяют увидеть, какую роль играют отдельные товары в среднем снижении цен на бытовую технику.

Аналогичным способом можно преобразовать в средние из индивидуальных индексы физического объема реализации:

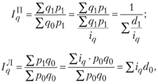
где 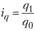– индивидуальные индексы физического объема.

Предлагаем читателю самостоятельно провести расчеты, что будет способствовать усвоению данного материала.

Индексы в форме средних из индивидуальных используют не только для характеристики изменения цен и физического объема, но и других (в основном качественных) показателей: себестоимости, производительности труда, рентабельности и т.д. При этом должно выполняться основное требование – их тождественность агрегатному индексу и реальность весов как экономических категорий. Например, индекс себестоимости разнородной продукции:

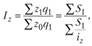
где 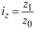– индивидуальные индексы производительности, исчисленные на основе трудоемкости единицы продукции; 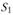– фактические затраты в денежном выражении на производство продукции в отчетном периоде.