Методология распределения с помощью складов
Складская сеть, через которую осуществляется распределение потоков, является одним из главных распределительных элементов логистической системы. Построение этой сети оказывает существенное влияние на издержки, возникающие в процессе доведения товаров до потребителей, а через них и на конечную стоимость реализуемого продукта. Наиболее эффективно процесс распределения может быть построен путем рассмотрения моделей организации распределения потоков с помощью складов (распределительных центров (рис. 4.11)).
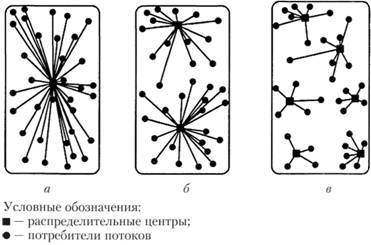
Рис. 4.11. Модели организации распределения потоков с помощью распределительных центров:
а – с одним распределительным центром; 6 – с двумя распределительными центрами; в – с шестью распределительными центрами
Для проведения анализа распределения выберем в качестве независимой переменной величину N – количество складов, через которые осуществляется снабжение потребителей. В качестве зависимых переменных будем рассматривать следующие виды издержек:
– транспортные расходы;
– расходы на ОГЛАВЛЕНИЕ запасов;
– расходы, связанные с эксплуатацией складского хозяйства;
– расходы, связанные с управлением складской системой.
Состав затрат, меняющихся при изменении количества складов в системе распределения и учитываемых при решении данной задачи, может быть иным. В каждом конкретном случае, определяя оптимальное количество складов в системе распределения, состав изменяющихся издержек должен быть обоснован на основе решения отдельной задачи.
Модели организации распределения существуют в трех вариантах: с помощью одного, двух или шести складов (см. рис. 4.11, а, б и в).
Рассмотрение вариантов моделей распределения необходимо производить при учете определенных условий:
– территориального расположения. В нашем случае территории функционирования моделей ограничиваются прямоугольниками одинакового размера;
– все цепи связи с потребителями потоков линейны и одноэтапны;
– место расположения потребителей потоков не меняется;
– каждый потребитель потока обследуется один раз;
– рассматриваются только вещественные потоки;
– обслуживание каждого потребителя потока производится только из центра;
– скорость транспортной доставки постоянна.
По транспортным расходам оценку моделей ведут с помощью построения зависимости величины затрат на транспортировку от количества складов в системе распределения.
Весь объем транспортных расходов по доставке товаров потребителям делят на две группы:
– расходы, связанные с доставкой товаров на склады системы распределения (эту категорию транспортных работ называют дальними перевозками).
– расходы по доставке товаров со складов потребителям (ближние перевозки).
Зависимости затрат на транспортировку от числа складов рассматриваются для каждой группы, после чего строятся графики этих зависимостей. Ввиду того что количество складов принимает целочисленное значение, графики имеют характер ломаных линий. Но при необходимости дискретные числовые значения затрат могут быть аппроксимированы кривыми непрерывными линиями, например кривыми второго порядка.
Итоговый анализ двух групп расходов показывает, что при увеличении количества складов в системе распределения стоимость доставки товаров на склады, т.е. стоимость дальних перевозок, возрастает, так как увеличивается количество поездок, а также совокупная величина пробега транспорта. Характер зависимости, представленной на рис. 4.12, показывает, что расходы по доставке растут медленнее, чем расстояние до складов 1-й, 2-й и 6-й групп. Например, при увеличении расстояния с 20 до 60 км (в три раза) расходы по доставке возрастают лишь в два раза. Причиной является устранение дополнительных операций по перегрузке товаров.

Рис. 4.12. Типовой график зависимости затрат по доставке товаров на склады от их количества
Другая часть транспортных расходов – стоимость доставки товаров со складов потребителям – с увеличением количества складов снижается (рис. 4.13), также по ломаной линии, так как сокращается длина цепей доставки товара.
Представленные на рис. 4.12 и 4.13 зависимости носят ориентировочно-типовой характер, так как их форма значительно зависит от территориальной расположенности потребителей потоков и распределительных центров. Для более точной оценки таких моделей по суммарным транспортным расходам необходим сравнительный анализ цепей доставки, скоростей по ним, объемов грузов и т.д. Такие задачи в транспортной логистике носят название "транспортной задачи" ("задачи коммивояжера") и решаются с помощью методов линейной и пространственной геометрии.

Рис. 4.13. Типовой график зависимости затрат по доставке товаров со складов потребителям потоков от количества складов
Приближенный комплексный анализ трех вариантов моделей организации распределения потоков с помощью распределительных центров (см. рис. 4.11) показывает, что в случае принятия варианта а (один распределительный центр) транспортные расходы по доставке будут наибольшими. Вариант в предполагает наличие шести распределительных центров, максимально приближенных к местам сосредоточения потребителей материального потока. В этом случае транспортные расходы по товароснабжению будут минимальными. Однако появление в системе распределения пяти дополнительных складов увеличивает эксплуатационные расходы, затраты на доставку товаров на склады, на управление всей распределительной системой. Не исключено, что дополнительные затраты в этом случае могут значительно превысить экономический выигрыш, полученный от сокращения пробега транспорта, доставляющего товары потребителям. Поэтому, возможно, предпочтительнее окажется вариант б, согласно которому район обслуживается двумя складами.
Как видим, при изменении количества складов в системе распределения часть издержек, связанных с процессом доведения потоков до потребителя, возрастает, а часть снижается. Это позволяет ставить и решать задачу поиска оптимального количества складов. Здесь также не учитываются затраты по созданию и эксплуатации распределительных складских систем, так как они сильно зависят от условий их места расположения, затрат на сооружение склада и т.д. Эти затраты увеличиваются с увеличением количества складов.
Анализ затрат на хранение запасов ведется по зависимости затрат на ОГЛАВЛЕНИЕ запасов от количества складов в системе распределения.
Так, на рис. 4.11, а снабжение всех потребителей осуществляется из одного склада. Увеличивая число складов, мы тем самым сокращаем зону обслуживания каждого из них, а при переходе к модели обслуживания, представленной на рис. 4.11, в в виде шести складов, зона, обслуживаемая одним складом, уменьшается примерно в шесть раз. Сокращение зоны обслуживания влечет за собой и сокращение запасов на складе. Однако запас сокращается, как правило, не столь быстро, как зона обслуживания. Причин тому может быть несколько. Например, необходимость содержания страхового запаса. В модели с одним складом страховой запас необходимо иметь в одном месте. Увеличение складской сети влечет за собой синхронное увеличение запаса, т.е., создавая шесть складов, необходимо в каждом из них создать страховой запас. В результате суммарный запас во всех шести складах возрастет (по сравнению с запасом в распределительной системе с одним центральным складом), правда, можно изменить порядок обслуживания потребителей, скажем, с другого склада и т.д.
Потребность складов в некоторых группах товаров при уменьшении зоны обслуживания может оказаться ниже минимальных норм, по которым товар получают сами склады. Это вынудит завозить данную группу на склады в количестве, большем потребности, что также повлечет за собой рост размера запаса. Можно привести и другие причины того, что при увеличении количества складов совокупный размер запаса в системе распределения увеличивается.
Графически характер зависимости затрат на ОГЛАВЛЕНИЕ запаса от количества складов в системе распределения может быть представлен такой же линией типовой зависимости затрат по доставке товаров на склад (см. рис. 4.12), если по вертикальной оси графика отложить затраты на ОГЛАВЛЕНИЕ запасов. Зависимость затрат, связанных с эксплуатацией складского хозяйства, от количества складов в системе распределения применяют, когда хотят оценить эксплуатационные расходы на складах. Эту оценку производят по удельным эксплуатационным затратам. Здесь учитывают, что при увеличении количества складов в системе распределения затраты, связанные с эксплуатацией одного склада, снижаются. Однако совокупные затраты распределительной системы на ОГЛАВЛЕНИЕ всего складского хозяйства возрастают. Происходит это в связи с так называемым эффектом масштаба: при уменьшении площади склада эксплуатационные затраты, приходящиеся на один квадратный метр (удельные эксплуатационные затраты), увеличиваются. Например, в торговле при уменьшении площади склада с 10,5 тыс. кв. м до 1,5 тыс. кв. м, т.е. в 7 раз, эксплуатационные затраты уменьшаются всего лишь в 5,25 раза. Замена одного склада шестью (общая площадь остается той же – 10,5 тыс. кв. м) повлечет за собой увеличение эксплуатационных расходов в 1,4 раза. Зависимость величины удельных эксплуатационных расходов от размера склада сферы торговли товарами народного потребления может быть получена из табл. 4.1.
Таблица 4.1
Удельные эксплуатационные затраты в зависимости от размера складской площади
|
Складская площадь, кв. м |
Удельные эксплуатационные затраты, усл. ден. ед. |
|
1500 |
60 |
|
3000 |
53 |
|
5750 |
49 |
|
10 500 |
45 |
|
13 000 |
39 |
В общем виде графически зависимость между количеством складов в системе распределения и размером эксплуатационных затрат может быть представлена такой же ломаной линией, как и на затраты по доставке товаров (ОГЛАВЛЕНИЕ запасов), изображенной на рис. 4.12.
Расходы по управлению распределительной системой с множеством складов определяют по зависимости затрат на управление распределительной системой от количества входящих в нее складов.
Характер аппроксимированных типовых зависимостей представлен на рис. 4.14. Здесь также действует эффект масштаба, в связи с чем при увеличении количества складов кривая затрат на системы управления делается более пологой в условиях применения ЭВМ для операционной обработки документации и моделирования и резко возрастает при ручной обработке информационных потоков.
Обязательным условием возможности эффективного функционирования распределительной системы, имеющей несколько складов, является компьютеризация управления складским хозяйством. При отсутствии средств вычислительной техники кривая расходов на управление может принять совершенно иной вид (штриховая кривая на рис. 4.14), т.е. увеличение количества складов повлечет за собой резкое увеличение затрат на систему управления складским хозяйством. Следует отмстить, что развитие распределительных складских систем в середине прошлого столетия сдерживалось именно отсутствием средств автоматизированной обработки информационных потоков.

Рис. 4.14. Аппроксимированные типовые зависимости затрат по управлению распределительной системой от количества входящих в нее складов
Аппроксимированные типовые зависимости совокупных затрат на функционирование системы распределения и затрат на отдельные процессы от количества входящих в нее складов, полученные путем сложения всех предыдущих графиков, приведены на рис. 4.15. Абсцисса минимума кривой совокупных затрат дает оптимальное значение количества складов в системе распределения (в нашем случае – четыре склада).
Ранее при решении задачи определения оптимального количества складов в системе распределения в качестве одной из главных зависимых переменных были рассмотрены транспортные расходы по доставке товаров потребителям потоков со складов распределительной системы. Изменение этой величины изучалось в зависимости от изменений количества складов в системе распределения. Однако величина транспортных расходов может существенно меняться не только в зависимости от количества складов, но также и в зависимости от места расположения этих складов на обслуживаемой территории.

Рис. 4.15. Аппроксимированные зависимости совокупных затрат на функционирование системы распределения и затрат на отдельные процессы от количества входящих в нее складов
Значительную зависимость транспортных издержек по товароснабжению от расположения распределительного центра иллюстрирует пример, приведенный на рис. 4.16. Представленная здесь модель системы распределения содержит один склад, который, очевидно, целесообразно разместить в центре района (вариант а), а не на окраине (вариант б).

Рис. 4.16. Варианты размещения распределительного центра на обслуживаемой территории:
а – рациональный; б – нерациональный (пробег транспорта увеличен в 1,75 раза)
Задача размещения распределительного центра приобретает актуальность при наличии развитой транспортной сети и территориальной свободы выбора места расположения распределительного центра. Например, если на территории района есть только две пересекающиеся магистрали, вдоль которых расположены все потребители, то, очевидно, распределительный центр целесообразно разместить на пересечении магистралей.
Задача размещения распределительных центров может быть формализована как поиск оптимального решения или же как поиск субоптимального (близкого к оптимальному) решения. Наукой и практикой выработаны разнообразные методы решения задач обоих видов.