Место четырехмерия и кривизны в теории относительности
Начнем с рассмотрения вопроса о месте четырехмерия в теориях относительности: относится ли оно к модельному или математическому слою (см. схему (9.2.1)).
Через три года после создания А. Эйнштейном СТО математик Г. Минковский, после введения своей геометрии, провозгласил: "Отныне пространство само но себе и время само но себе должно обратиться в фикции и лишь некоторый вид соединения обоих должен еще сохранять самостоятельность" [23, с. 167]. К чему следует относить это высказывание: к физической реальности или лишь к математическому приему или аппарату? Подавляющее большинство физиков и философов солидарны с Минковским[1]. Однако так ли уж тут все однозначно?
Начнем с СТО. Суть применения геометрии Минковского связана с тем, что в СТО расстояния и интервалы времени зависят от системы отсчета, а если ввести понятие четырехмерного "события" (состоящего в том, что физический объект находится в данном месте трехмерного пространства в данный момент времени), то можно составить инвариантную для всех инерциальных систем отсчета комбинацию вида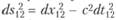 
, где с – скорость света; dt12 – интервал времени между событиями "1" и "2"; dx12 – расстояние между точками, отвечающими событиям "1" и "2". В силу инвариантности величины ds12, называемой "интервалом" между событиями "1" и "2", "четырехмерное пространство[2] событий", о котором говорит Минковский в своей статье 1908 г., оказывается очень удобным[3].
По этому поводу А. Пайс пишет: "Так началось великое формальное упрощение СТО. Вначале это не произвело на Эйнштейна большого впечатления, он счел запись своей теории в тензорной форме “излишней ученостью”" [21, с. 148]. И действительно, все три основных кинематических эффекта" СТО – сокращение длин, замедление времени и относительность одновременности – есть, в первую очередь, следствие изменения главного эталона в процедурах измерения (|И} на схеме 9.2.1). То есть для понимания СТО четырехмерия не требуется. То есть в СТО четырехмерие, о котором говорит Г. Минковский, относится к математическому представлению (математическому слою схемы 9.2.1), это еще одно математическое представление, после исходного эйнштейновского 1905 г. Так его Эйнштейн поначалу и воспринял.
Посмотрим теперь, что происходит с ответом на поставленный вопрос в ОТО. В ОТО Эйнштейн, используя принцип относительности гравитации и ускорения, утверждавший, что локально действие любого гравитационного поля эквивалентно действию соответствующего ускорения (опыт в лифте), сводит гравитацию к изменению метрики, сводя гравитацию к кривизне. При этом, хотя "опыт в лифте" относится к обычному трехмерному пространству, изменение метрики в виде кривизны Эйнштейн вводит в четырехмерном пространстве-времени Минковского. Согласно А. Пайсу в 1912 г. Эйнштейн "усвоил тензорные методы, а в 1916 г. выразил признательность Минковскому за то, что тот значительно облегчил переход от СТО к общей теории относительности" [21, с. 148]. Действительно, уравнения Эйнштейна в ОТО выражены на языке четырехмерного пространства событий, в котором, по сути, к четырехмерию Минковского добавлена кривизна Римана.
В результате в ОТО поставленные в конце параграфа 14.1 вопросы можно, исходя из схемы 9.2.1, переформулировать так: 1) является ли кривизна математическим образом гравитационного поля или гравитация сводится к кривизне (т.е. принадлежит ли кривизна математическому или модельному слою); 2) если второе, то физическим смыслом надо наделять искривление в четырехмерном пространстве-времени или в обычном трехмерном пространстве и одномерном времени?
Примером современной теории, дающей первый ответ на первый вопрос, является релятивистская теория гравитации (РТГ) академика А. А. Логунова [17], которая, по его словам, является "объединением идеи Пуанкаре о гравитационном поле [23] как о физическом поле в духе Фарадея – Максвелла с идеей Эйнштейна о римановой геометрии пространства-времени. Уравнения в данной теории существенно отличаются от уравнений Гильберта – Эйнштейна, поскольку в ней сохранено понятие инерциальной системы координат, а силы гравитации в принципе отличаются от сил инерции, так как они вызваны физическим полем". "Согласно этой теории гравитации однородная и изотропная Вселенная развивается циклически от большой плотности до минимальной и т.д., и может быть только плоской. Теория предсказывает существование во Вселенной значительной скрытой массы вещества. Существование во Вселенной “черных дыр” полностью исключается[4]. Теория объясняет все известные наблюдательные факты в Солнечной системе" [17, с. 187-189].
Логунов кладет в своей РТГ в качестве основания законы сохранения вместо эйнштейновского принципа эквивалентности инертной и тяжелой (гравитационной) массы. В моделях Ньютона или Логунова, моделях с силой или полем тяготения эта пропорциональность существует, но она не означает эйнштейновской эквивалентности инерционной и гравитационной масс. Для них, согласно Логунову, "силы гравитации принципиально отличаются от сил инерции"[5]. В работе [11] показывается, что для не слишком сильных нолей эйнштейновский подход через кривизну пространства-времени и полевой подход дают эквивалентные результаты.
Хотя мейнстрим придерживается концепции А. Эйнштейна, а не А. А. Логунова, аналогия между гравитационным и электромагнитным полями постоянно проскакивает и там. Например, в "Физическом энциклопедическом словаре" в статье "Гравитационные волны" мы читаем: "Гравитационные волны – это переменное гравитационное поле, которое излучается ускоренно движущимися массами, “отрывается” от своего источника и, подобно электромагнитному излучению, распространяется в пространстве со скоростью света" [26, с. 137]. "Гравитационную волну можно рассматривать как гравитационное поле, движущееся в пространстве. Такая волна должна была бы оказывать силовое воздействие на объекты, обладающие массой", – пишет Дж. Вебер [8, с. 179]. То есть здесь явно просматривается аналогия гравитационной и электромагнитной волн, а за ней и аналогия гравитационного и электромагнитного полей. Только если состояние электромагнитного поля определяется значениями напряженностей электрического и магнитного полей, измеряемых пробными зарядами и петлями тока, то состояние "гравитационного поля" определяется значениями ускорения и ряда пространственных производных ускорения пробного массивного тела в различных точках пространства. Правда, Дж. Вебер добавляет: "Физик-релятивист говорит о гравитационной волне как о распространении кривизны пространства- времени", но тут же уточняет, что "более точным было бы, по-видимому, такое определение: гравитационная волна – это возмущение гравитационного поля, распространяющееся с конечной скоростью и несущее с собой энергию".
Другой пример – репрезентативное для ОТО явление – "гравитационный коллапс", который в "Физическом энциклопедическом словаре" описывается как "процесс гидродинамического сжатия тела под действием собственных сил тяготения" [26, с. 137] в обычных трехмерном пространстве и одномерном времени (приблизительно то же мы найдем в работе 15, т. 2, с. 417]). Более того, на том же языке классической модели (но используя постулат ТО о наличии максимальной физической скорости) мы можем получить даже выражение для шварцшильдовского радиуса, рассматривая его как границу, на которой вторая космическая скорость для данной звезды становится равной скорости света, в результате чего ее не может покинуть даже свет, и она превращается в черную дыру, из которой ничего не выходит.
Таким образом, хотя общепринятым считается второй ответ на первый вопрос – гравитация сводится к кривизне[6], альтернативный (первый) ответ – кривизна является математическим образом гравитационного поля – окончательно со сцены не сошел.
Теперь обратимся ко второму вопросу – о месте четырехмерности пространства-времени. Для ответа на него рассмотрим: 1) как строится уравнение движения для конкретных случаев; 2) как описываются характерные для ОТО эффекты; 3) что измеряется в ОТО, в частности, в случае попыток зафиксировать "гравитационные волны".
В целом типичная процедура постановки и решения задачи в ОТО выглядит следующим образом. Берут "затравочную классическую систему", которая состоит из одного или нескольких выделенных изучаемых тел (или непрерывной среды, или электромагнитного поля) и источников гравитационного поля – массивных тел и полей, распределенных в обычных трехмерном пространстве в определенный момент времени. Затем составляют для этой системы тензор энергии-импульса в четырехмерном пространстве-времени, который входит в уравнение, определяющее кривизну (точнее – метрику) в четырехмерном пространстве-времени ОТО[7]. Окончательный же результат (то, что выявляет эксперимент) в конце концов всегда представляют на языке движения тел в обычных трехмерном пространстве и одномерном времени.
Рассмотрим теперь на примере гравитационных волн процедуры измерения в ОТО. В работе [2] "гравитационная волна" представляется как "рябь на статической кривизне" (имеется в виду кривизна в четырехмерном пространстве-времени Римана), но когда говорят о ее источнике и конструировании прибора для ее регистрации в конкретном эксперименте, то речь уже идет о "распространении" в обычном пространстве и времени "градиента ускорений", источником которого являются вращающиеся (в обычном пространстве и времени) двойные звезды, а приемником – разнесенные в обычном пространстве тела, взаимное смещение которых "вызвано переменной силой (гравитации. – А. Л.)".
Приводимые в оправдание таких описаний ссылки на необходимость все измерения выражать на "классическом" языке, с нашей точки зрения, нс выдерживают критики, поскольку существуют описания последовательных процедур измерения величин, фигурирующих в геометрии пространства-времени Римана (см. статью Р. Мацке в работе [8] (потенциал человеческого языка и мысли велик и понятие "классического" исторично)). Неверными нам представляются и ссылки на то, что такие непоследовательные описания являются приближениями и упрощениями. Ведь точность этих описаний ничем не ограничена. По сути последовательная с точки зрения Эйнштейна исследовательская программа (в терминологии И. Лакатоса, описанной в гл. 6) должна была бы реализовывать описанный Р. Мацке способ измерения величин, непосредственно отвечающих четырехмерному пространству-времени Римана, но этот способ столь сложен, что не выдерживает конкуренции с описанным выше и реально применяемым на деле более простым подходом с более простыми физическими моделями (где четырехмерное пространство-время Римана относится лишь к математическому слою).
Наконец, рассмотрим специфический для ОТО эффект – течение времени в двух системах отсчета при падении тела на "черную дыру": связанной с падающим телом (в ней тело проходит сферу Шварцшильда и продолжает падать к центру "черной дыры") и внешней (где время замедляется до бесконечности при приближении тела к сфере Шварцшильда [15, т. 2]). Тут проявятся эффекты ОТО, но это по тину те же эффекты, что и в СТО, – разница в течении времени (ходе часов) и длине линейки, которые в ОТО зависят не только от относительной скорости систем отсчета, но и от ускорения и гравитационного поля. Остается в силе и главный кинематический постулат СТО – постоянство скорости света (имеется в виду ее скалярное значение, в ОТО свет распространяется не прямолинейно).
По сравнению с СТО в ОТО ситуация осложняется тем, что если в СТО одна система отсчета (один набор линеек и часов) действовала во всем пространстве, то в ОТО в каждой локальной области пространства надо, вообще говоря, вводить свою систему отсчета со своими линейками и часами, поскольку свойства (метрика) пространства и времени меняются и во времени, и от точки к точке. Но и здесь для описания (а не вычисления) самого явления не надо "перемешивать" пространство и время. Это утверждение созвучно позиции П. Дирака. Он предлагает исходить из гамильтоновой формы, которая "помогает отделить физически существенные динамические переменные от тех, которые лишь описывают координатную систему", и в которой основным понятием является понятие "состояние в данный момент времени". "В релятивистской теории под этим понимается состояние на некоторой трехмерной пространственно- подобной поверхности общего вида в пространстве-времени", т.е. четырехмерие распадается на (3+1)-мерие без ограничения точности для уравнения движения. "Представляется вполне допустимым рассматривать гамильтонианов формализм как основной; тогда в теории не было бы никакой четырехмерной симметрии" [10][8].
Итак, в ОТО, как и в СТО, четырехмерное пространство-время выступает как математическое представление, в котором задается уравнение метрики пространства и времени, а в модельном слое мы имеем те же, что и в классической физике, модели двигающихся механических массивных тел и электромагнитного поля в обычных трехмерном пространстве и времени, но с другой метрикой (и с несколько иным уравнением движения), а следовательно, и движением, и другими процедурами измерения, приводящими к относительности длин, интервалов времени, одновременности. При этом в ОТО состояние выделенных изучаемых тел (или непрерывной среды и электромагнитного поля) задается, как в классической механике, – их положениями и импульсами в обычном трехмерном пространстве и обычном времени (то же можно сказать про механику сплошных сред и электродинамику)[9].
В заключение этого параграфа еще одно замечание философского плана. В физике XX в. возникает довольно интересная картина, характерная для теории относительности и квантовой механики: "парадигма" (в куновских понятиях – см. параграф 6.4), о которой говорит сообщество физиков, оказывается отличной от "парадигмы", которой физики следуют в своей работе. В ТО физики говорят о неразрывном пространстве-времени в духе Минковского, а на поверку описывают явления в обычном 3+1-мерном мире[10]. В квантовой механике (см. гл. 15), говорят в духе "копенгагенской" интерпретации, а работают в другой, в которой состояние существует до и независимо от измерения, как и положено в физике.