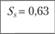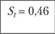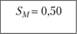Мера Дженсена

Дженсен подходил к исследованию результатов инвестиционной деятельности, оценивая превышения доходности портфеля ri,t над безрисковой доходностью 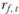в каждый момент рассматриваемого периода (в нашем случае – за последние три года). Мера Дженсена, обозначаемая 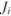, есть не что иное, как свободный член в регрессионном уравнении, описывающем линейную регрессию превышения (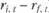) рассматриваемого портфеля на превышения (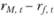) рыночного портфеля:

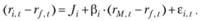
Мера Дженсена может быть вычислена двумя способами:

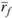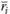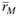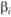а) если определены средние значения , , и , то

б) в другом случае можно брать наблюдавшиеся значения 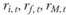, положим, за каждый месяц предшествующих трех лет, вычислять превышения 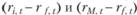, подставлять их в регрессионную формулу и вычислятькак свободный член регрессии. Возможность прямого вычисления меры Дженсена как свободного члена регрессии является одним из главных преимуществ метода Дженсена. Затем мера 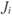сравнивается с мерой 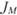рыночного портфеля, которая равняется нулю.

Способность менеджера превысить показатели рыночного портфеля будет выражаться тем, что мера 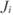станет больше нуля, а при неудачах менеджера мера станет отрицательной.

Если на графике отложить по вертикальной оси значения превышений 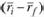, а по горизонтальной – портфельную бету βi, то графически линия SML (по реализованным данным) в этих координатах пройдет через начало координат (рис. 5.2).

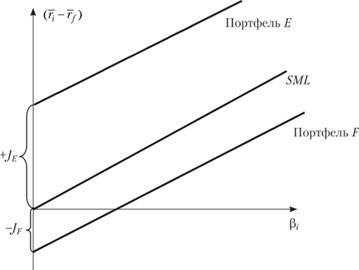
Рис. 5.2. Графическая интерпретация меры Дженсена

По вертикальной оси на этом графике откладываются величины превышения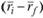. Линия, соответствующая ры-

ночному портфелю, проходит через начало координат. Портфель Е имеет положительную величину 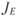, поэтому его соотношение риск/доходность превосходит рыночное, а вот портфель F управляется не совсем удачно, так как его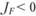

В таком случае каждый раз, когда оцениваемый портфель имеет 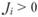и соответствующая линия проходит выше рыночной, отсекая положительный отрезок на вертикальной оси (как для условного портфеля Е), деятельность менеджера такого портфеля надо оценивать положительно. При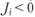(как для условного портфеля F) деятельность менеджера рассматривается как неудачная.

Мера Шарпа

Шарп предложил оценивать портфель с помощью меры 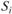, показывающей соотношение превышения средних величин 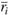над 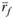, т.е. 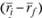, и суммарного (а не систематического) риска портфеля, выражаемого стандартным отклонением:

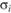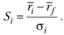
Значит, можно считать, что мера Шарпа показывает, как изменяется превышение 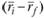при изменении суммарного риска портфеля на единицу.

Для рыночного портфеля М величина меры Шарпа

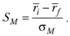
Именно с этой величиной необходимо сравнивать меру Шарпа для каждого портфеля: чем выше 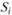и чем значительнее она превышает 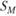, тем более удачные результаты портфеля.

Проиллюстрируем использование меры Шарпа на условном примере трех портфелей R, S, Т, соответствующие данные по которым приведены в табл. 5.5.

Меры Шарпа для каждого портфеля вычисляются так:

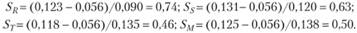
Как следует из табл. 5.5, портфели R и S доминируют над рыночным портфелем, так как 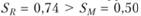и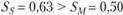

Таблица 55

Вычисление меры Si для трех условных портфелей

Параметры	Портфели
	R	5	Т	Рыночный
	0,123	0,131	0,118	0,125
	0,090	0,120	0,135	0,138

Сравнение мер Трейнора, Дженсена и Шарпа

Несмотря на то что все три меры выведены с использованием теории САРМ, они могут дать несовпадающие результаты при оценке портфелей, поскольку результаты применения каждой меры зависят от характеристик портфелей, которые подлежат анализу.

Так, меры Трейнора и Дженсена дают абсолютно идентичные результаты, если оценивать какой-то портфель по отношению к рыночному портфелю: если мера Дженсена JK для К-го портфеля положительна, значит, мера Трейнора ТK больше рыночной меры Трейнора ТM. Соответственно на графике (рис. 5.3) линия возможных портфелей, проходящая через точку К, лежит выше линии SML (построенной на фактических данных). Одновременно мера Дженсена Jk > 0, значит, обе меры показывают, что портфель К доминирует над рыночным портфелем.

Однако меры Трейнора и Дженсена могут дать противоположные результаты, если с их помощью ранжировать портфели, т.е. пытаться определить, какой из портфелей К или L (оба превосходящие рыночный) является доминирующим. Это объясняется тем, что данные меры по-разному учитывают систематический риск: в модели Трейнора коэффициент "бета" выводится путем регрессии реальных данных ri,t на rm,t, а в модели Дженсена – путем регрессии превышений (ri,t – rf,t) на превышения (rM,t – rf,t). В связи с этим меру Дженсена не следует применять для ранжирования портфелей, особенно, если риск портфелей сильно отличается.

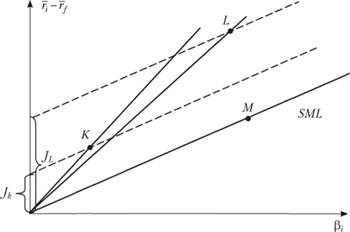
Рис. 5.3. Сравнение мер Трейнора и Дженсена^[1]

Например, сравним два портфеля К и L (см. рис. 5.3). Какой из них лучше? Если следовать мере Дженсена, то лучше портфель L, так как ero JL > JK. Однако это неверно, и линии возможных портфелей опровергают подобное заключение, поскольку композиционные портфели, составленные из портфеля К плюс безрисковое суживание, или заем, всегда доминируют над аналогичными портфелями, составленными на основе портфеля L.

Еще большие различия может дать использование меры Шарпа. Например, можно подобрать такие портфели, что для них мера Трейнора будет свидетельствовать о превосходстве над рыночным портфелем, а мера Шарпа – наоборот, о превосходстве рыночного портфеля. Все объясняется тем, что в модели Шарпа учитывается суммарный, а не только систематический риск. Если портфель достаточно диверсифицирован и суммарный риск приближается к рыночному риску, то все три меры дадут совпадающие результаты. Однако если менеджер в попытке превысить рыночный портфель начнет приобретать недооцененные средства и продавать переоцененные, то диверсификация может снизиться и диверсифицируемый риск станет влиять на оценки портфеля. В результате меры Дженсена и Трейнора могут показать, что портфель доминирует над рыночным, а мера Шарпа – что нет.

Чем же руководствоваться в таком случае? Как это ни покажется странным, но все будет определяться тем, какую долю в общем состоянии инвестора занимают инвестиционные расходы. Если они составляют почти все его состояние, то надо руководствоваться мерой Шарпа. Когда же инвестируется небольшая часть состояния – мерой Трейнора или Дженсена. Считается, что деятельность новых менеджеров лучше оценивать по мере Трейнора. Мера же Дженсена лучше подходит при сравнении портфелей с мало отличающимися уровнями риска.