Машинное обучение
Термин "машинное обучение" возник в 1960-е гг., когда только появились большие ЭВМ, которые старшее поколение уважительно называло "машинами". Это словосочетание до сих пор употребляется в среде специалистов, отдающих дань уважения своим предшественникам, однако в наши дни оно требует некоторого пояснения, хотя бы в силу того, что термин в английском языке означает что угодно (например, станок), но не компьютер.
В первую очередь, следует иметь в виду, что "машина" — это сегодняшний суперкомпьютер. "Машинное обучение" заключается не в передаче знаний с помощью компьютера, а в обучении компьютера. Во-вторых, "научить" компьютер можно разными способами, например, введя в него требуемое программное обеспечение. Здесь мы будем говорить не об обучении, а о "самообучении" компьютера, для которого применяются методы и алгоритмы, описываемые ниже.
Таким образом, машинное обучение является перспективным современным направлением в области извлечения знаний из хранилищ данных — это подраздел искусственного интеллекта, включающий методы построения алгоритмов, способных обучаться.
Машинное обучение имеет специфику, связанную с проблемами вычислительной эффективности и переобучения. Целью машинного обучения является частичная или полная автоматизация решения сложных профессиональных задач в самых разных областях человеческой деятельности.
Различают два типа обучения:
— обучение по прецедентам, или индуктивное обучение; основано на выявлении общих закономерностей по эмпирическим данным;
- дедуктивное обучение предполагает формализацию знаний экспертов и построение баз знаний. Дедуктивное обучение принято относить к области экспертных систем.
Сфера применений машинного обучения постоянно расширяется. Повсеместная информатизация приводит к накоплению огромных объемов данных в науке, производстве, бизнесе, транспорте, здравоохранении. Возникающие при этом задачи прогнозирования, управления и принятия решений часто относят к задачам обучения по прецедентам.
Метод опорных векторов
Одной из наиболее популярных методологий машинного обучения по прецедентам является построение машины опорных векторов, известной в англоязычной литературе под названием SVM (Support Vector Machine). Этот тип методов статистического оценивания функций (или новый вид обучаемых машин) был предложен в середине 1990-х гг. Основы подхода заложены в работах В. Н. Ванника по статистической теории обучения. SVM-алгоритмы приобрели популярность благодаря многим привлекательным свойствам и перспективным практическим приложениям (в биоинформатике — при обработке информации огромных объемов; в области экономики и бизнеса — для прогнозирования временных рядов, оценивания кредитоспособности, а также в сфере финансовой безопасности). SVM-подход к задаче восстановления регрессии преодолевает "проклятие размерности". Источником повышения эффективности SVM-алгоритмов являются оптимальные схемы распределения памяти и эффективные вычислительные процедуры.
Общая модель обучения по эмпирическим данным предполагает наличие: генератора случайных векторов х, появляющихся независимо согласно фиксированному, но неизвестному распределению вероятностей Р(х); учителя, определяющего выход у для любого входящего х, согласно условному распределению Р(у/х), также фиксированному и неизвестному; класса функций {/(х, а)}, где параметр а может принимать значения из некоторого допустимого множества произвольной природы.
Задача обучения состоит в выборе из заданного множества функций одной, которая предсказывает ответ учителя наилучшим образом. Этот выбор должен быть основан на тренировочной последовательности конечного объема (/), т.е. независимых, одинаково распределенных согласно закону Р(х, у) = Р(х) х Р(у/х) наблюдениях (х„ #,).....(х,, г/,).
Наилучшая функция /, которую можно выбрать, -функция, минимизирующая ожидаемый риск Щ/ = = j L(f (х), y)dP(x, у), где L — содержательно обоснованная функция потерь (ФП). Поскольку распределение Р(х, у) неизвестно, можно, руководствуясь индукционным принципом минимизации эмпирического риска, заменить среднее по мере Р(х, у) средним по тренировочным данным: 1 /
R,mpf = j^L(f(xi)-ui)- Однако для конечных выборок этот ' 1=1
принцип оказывается несостоятельным, поскольку может приводить к переобучению (oveifitting).
Статистическая теория обучения предлагает новый индукционный принцип для обучения по конечным выборкам — структурную минимизацию риска. Сущность этого принципа состоит в минимизации верхней границы ожидаемого риска, что обеспечивает согласованность между качеством обучения и сложностью класса аппроксимирующих функций. Верхняя граница ожидаемого риска, основанная на такой мере сложности функций, как УС-размерность (я), имеет вид
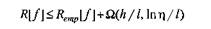
и гарантирована с вероятностью 1 — т| для любого т|€(0, 1) и любой функции / из класса {/(х, а)} с УС- размерностью И.
Принцип структурной минимизации риска оснащает ЭУ- машины способностью к обобщению, которая и является целью статистического обучения.
Выбор функции потерь определяет различные методы обучения. Вид функции потерь связан с априорными предположениями о распределении шума в регрессионной модели.
Рассмотрим метод опорных векторов для решения задачи восстановления регрессии
1. е- нечувствительная функция потерь.
Пусть (х,,у),...,(х/,у/)еЛих/г — тренировочная последовательность. Требуется найти наиболее гладкую функцию /(х), величина отклонения значений которой от наблюдаемого у по всей тренировочной последовательности не превышает заданное число е. Будем искать линейную оценку функции регрессии в виде: /(х) = (у/, х) Е",Ь Е. Мерой гладкости класса функций может служить евклидова норма |<яг|.
Для ослабления жестких ограничений введем переменные . Тогда, согласно принципу структурной минимизации риска, задача восстановления регрессии сводится к задаче оптимизации:
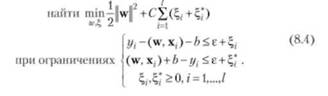
Параметр регуляризации С > 0 устанавливает баланс между допустимой величиной ошибки и сложностью класса функций, в котором ищется решение /(х). Формулировка этой задачи оптимизации соответствует использованию
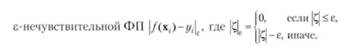
Прямая задача в терминах функции Лагранжа для задачи (8.4) представляет собой задачу квадратичного программирования. Целесообразно решать эквивалентную ей двойственную задачу:
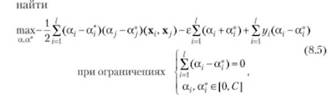
где а,, а' — множители Лагранжа.
Условия оптимальности Карунта — Куна — Таккера (ККТ) в этом случае будут необходимыми и достаточными. Условия ККТ позволяют найти вектор XV с использованием только тренировочной последовательности w = X( , а г)";. Такой вид вектора весов называют ЗУ разложением. Тогда решение
БУИ-задачи будет иметь вид: /(х) = £( , а ^<к,-. х) Ь.+
И в процессе обучения, и при прогнозировании входные векторы появляются только в виде скалярных произведений, что обеспечивает обобщение рассмотренной процедуры на нелинейный случай. Векторы тренировочной последовательности нелинейно отображаются в пространство признаков сколь угодно большой размерности. Для гильбертовых пространств с репродуктивным ядром существует высокоэффективный прием вычисления скалярных произведений, который состоит в использовании ядерных функций. Поэтому любой линейный алгоритм, использующий только скалярные произведения, может быть неявно выполнен в пространстве признаков, надо лишь каждое скалярное произведение заменить нелинейным ядром. Процесс обучения для нелинейной задачи восстановления регрессии аналогичен процессу решения линейной задачи, но скалярные произведения (х, х') заменяются значениями ядра к(х,х'). и вектор w теперь принадлежит пространству признаков. Ряд теорем устанавливает, какие функции k соответствуют скалярному произведению в различных пространствах признаков, т.е. являются допустимыми SV-ядрами. Примером удачного выбора ядра в общем случае может служить гауссовское ядро. Из условий ККТ следует: только образцы, для которых а.р=С, лежат вне е-области вокруг/(х); <х,<х*=0 для всех г; для <хРе(0, С) соответствующие £Р=0, при этом легко можно вычислить сдвиг Ь; для всех входных векторов, лежащих внутри е-области, а.р = 0, что свидетельствует о разреженности SVR-решения. (Здесь q("> обозначает как переменную С,, так и £*•) Таким образом, в SV-разложение войдет только часть векторов тренировочной последовательности. Они и являются опорными векторами.
Рассмотрим основные подходы к построению SVR-машин в случае е-нечувствительной функции потерь. Непосредственное решение задачи квадратичного программирования (8.5) часто невозможно из-за ее большой размерности. Для большинства других выпуклых функций потерь не существует явного решения подзадачи квадратичного программирования размерности два.
Пошаговое SVM-обучение на новых данных путем отбрасывания всех членов предшествующей тренировочной последовательности, кроме полученных опорных векторов, даст только приближенное решение. Алгоритм Incremental updating (IU) предполагает onlinc-режим поступления образцов и нечувствительную функцию потерь. За конечное число шагов алгоритм приводит к выполнению условий ККТ как для всех предшествующих данных, так и для вновь поступившего образца. Это достигается путем изменения ключевых переменных системы за счет наибольшего возможного приращения двойственной переменной, соответствующей новому образцу. Алгоритм Successive overrelaxation (SOR) для решения задачи восстановления регрессии при использовании е-нечувствительной функции потерь нс решает проблему квадратичного программирования. Если добавить к целевой функции SVR-задачи переменную Ь/2 и минимизировать полученную функцию по w, ^ и Ь, то двойственная задача минимизации лагранжиана не будет иметь ограничения типа равенств и ее можно свести к задаче решения системы линейных алгебраических уравнений (СЛАУ). SOR-алгоритм решает СЛАУ методом последовательной верхней релаксации.
2. Квадратичная функция потерь.
Использование квадратичной функции потерь приводит к задаче оптимизации:
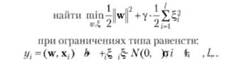
что соответствует гребневой регрессии, а минимизация эмпирического риска — методу наименьших квадратов. Задача сводится к СЛАУ порядка (/+ 1) с вектором неизвестных (а, Ь), где а — вектор множителей Лагранжа. При этом не изменяется вид 8УК-машины: /(х)(*£ ;(х^ х) к
/=|
БУМ-решение, построенное на основе квадратичной функции потерь, в общем случае абсолютно плотно: а, * О для всех и Таким образом, реализация метода требует настолько больших временных затрат и такого объема памяти, что метод становится непригодным для практического использования.
Для получения разреженной аппроксимации полного ядерного разложения применяют алгоритмы, основанные на идее последовательного наращивания множества опорных векторов. Основное преимущество этого подхода заключается в том, что не требуется решать полную ЯУ- проблему: на каждом шаге определяется необходимость включения очередного входного вектора в ядерное разложение.
Итерационный жадный SVR-алгоритм GSLS (Greedy Sparse Least Squares) позволяет получить разреженную аппроксимацию полного SV-разложения, включая на каждом шаге в SV- разложение тренировочный образец, минимизирующий регуляризованный эмпирический риск. Пусть вектор весов w аппроксимируется взвешенной суммой ограниченного подмножества векторов тренировочной последовательности, т.е. SV-разложение представляет собой
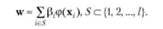
Тогда целевая функция, подлежащая минимизации, будет иметь вид
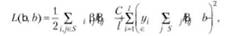
Где *£=.К(Х;,Х,).
Приравняв частные производные L по ß и b нулю, получим систему |S|+1 линейных уравнений с |S|+1 неизвестными.
Начиная с параметра смещения Ь, разреженная SVR-машина строится итеративно. На каждой итерации матрица системы расширяется за счет добавления одной строки и одного столбца, соответствующих тренировочному образцу, включенному в ядерное разложение на предыдущем шаге. Обращение расширенной блочной матрицы производится рекурсивно. Обучение машины завершается, когда ядерное разложение (|S|) достигает заранее заданного размера или когда величина приращения целевой функции L становится меньше заданного порогового значения.
KRLS (Kernel Recursive Least Squares) - online-алгоритм для задачи восстановления регрессии, также основанный на использовании квадратичной функции потерь. В отличие от стандартной задачи SVR, для которой разреженность решения достигается путем устранения образцов с нулевыми множителями Лагранжа, KRLS конструирует разреженное решение по мере поступления новых членов тренировочной последовательности. В SV-разложение включаются векторы, входящие в составленный согласно определенному критерию словарь. Вновь поступивший вектор добавляется в словарь в том случае, если он не является приближенной линейной аппроксимацией векторов, составляющих словарь к моменту его поступления.
3. Основные преимущества БУЯ-подхода.
Функция, оценивающая кривую регрессии, всегда имеет вид
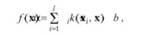
где к(х, х') — ядерная функция, соответствующая скалярному произведению в пространстве признаков. Переход из пространства образов в пространство признаков посредством некоторого отображения Ф целесообразен по следующим причинам:
— в качестве скалярного произведения удобно использовать ядерную функцию к(х, х') = ( <рх) -фх'));
— явный вид отображения Ф может быть неизвестен, достаточно знать и использовать ядро следовательно, можно строить различные обучающие алгоритмы, в том числе и нелинейные;
— в пространстве признаков нелинейную задачу обучения можно решать подобно линейной задаче.
Заданное множество аппроксимирующих функций представляет собой достаточно богатый класс нелинейных (в зависимости от вида ядра) функций. При этом они линейны по параметрам. Количество свободных параметров равно количеству опорных векторов и не зависит от размерности входных векторов. Благодаря свойству разреженности, присущему БУ- машинам, число опорных векторов значительно меньше объема тренировочной последовательности. Таким образом, метод опорных векторов для задачи восстановления регрессии можно применять при любом числе контролируемых факторов, поскольку он преодолевает "проклятие размерности".