Корреляционно-регрессионный анализ

Корреляционный анализ, как и другие статистические методы, основан на использовании вероятностных моделей, описывающих поведение исследуемых признаков в некоторой генеральной совокупности, из которой получены экспериментальные значения хi и уi. Когда исследуется корреляция между количественными признаками, значения которых можно точно измерить в единицах метрических шкал (метры, секунды, килограммы и т.д.), то очень часто принимается модель двумерной нормально распределенной генеральной совокупности. Такая модель отображает зависимость между переменными величинами хi и уi графически в виде геометрического места точек в системе прямоугольных координат. Эту графическую зависимость называются также диаграммой рассеивания, или корреляционным полем. Данная модель двумерного нормального распределения (корреляционное поле) позволяет дать наглядную графическую интерпретацию коэффициента корреляции, так как распределение в совокупности зависит от пяти параметров: mx, my – средние значения (математические ожидания); sx, sy – стандартные отклонения случайных величин X и Y, р – коэффициент корреляции, который является мерой связи между случайными величинами X и Y. Если р = 0, то значения хi, уi, полученные из двумерной нормальной совокупности, располагаются на графике в координатах х, у в пределах области, ограниченной окружностью (рис. 3.7, а).

Рис. 3.7. Графическая интерпретация взаимосвязи между показателями

В этом случае между случайными величинами X и Y отсутствует корреляция, и они называются некоррелированными. Для двумерного нормального распределения некоррелированность означает одновременно и независимость случайных величин X и Y.

Если р = 1 или р = -1, то между случайными величинами X и Y существует линейная функциональная зависимость (Y = с + dX). В этом случае говорят о полной корреляции. При р = 1 значения хi, уi определяют точки, лежащие на прямой линии, имеющей положительный наклон (с увеличением хi значения уi также увеличиваются), при р = -1 прямая имеет отрицательный наклон (рис. 3.7, б).

В промежуточных случаях (-1 < р < 1) точки, соответствующие значениям хi, уi, попадают в область, ограниченную некоторым эллипсом (рис. 3.7, в, г), причем при р > 0 имеет место положительная корреляция (с увеличением хi значения уi имеют тенденцию к возрастанию), при р < 0 корреляция отрицательная. Чем ближе р к ±1, тем уже эллипс и тем теснее экспериментальные значения группируются около прямой линии. Здесь же следует обратить внимание на то, что линия, вдоль которой группируются точки, может быть не только прямой, а иметь любую другую форму: парабола, гипербола и т.д. В этих случаях мы рассматривали бы так называемую нелинейную (или криволинейную) корреляцию (рис. 3.7, д). Таким образом, визуальный анализ корреляционного поля помогает выявить не только наличие статистической зависимости (линейную или нелинейную) между исследуемыми признаками, но и ее тесноту и форму. Это имеет существенное значение для следующего шага в анализе выбора s и вычисления соответствующего коэффициента корреляции. Корреляционную зависимость между признаками можно описывать разными способами. В частности, любая форма связи может быть выражена уравнением общего вида Y = f(X), где признак Y – зависимая переменная, или функция от независимой переменной X, называемой аргументом. Соответствие между аргументом и функцией может быть задано таблицей, формулой, графиком и т.д. Основные параметры корреляционно- регрессионного анализа представлены в табл. 3.9.

Таблица 3.9

Основные параметры корреляционно-регрессионного анализа

Параметр	Обозначение	Что характеризует параметр и для чего применяется	Оптимальное значение параметра
Объем выборки	т	Объем данных по фактору (размер матрицы по вертикали). Применяется для установления тенденций изменения фактора	Не менее чем в 3-5 раз больше числа факторов (nj). С увеличением числа факторов кратность должна увеличиваться
Коэффициент вариации	Vi	Уровень отклонения значений факторов от средней анализируемой совокупности	Меньше 33%
Коэффициент парной корреляции	rху	Тесноту связи между фактором и функцией. Применяется для отбора факторов	Больше 0,1
Коэффициент частной корреляции	rхх	Тесноту связи между факторами. Применяется для отбора факторов	Чем меньше, тем лучше модель
Коэффициент множественной корреляции	R	Тесноту связи одновременно между всеми факторами и функцией. Применяется для выбора модели	Больше 0,7
Коэффициент множественной детерминации	D	Долю влияния на функцию включенных в модель факторов. Равен квадрату коэффициента множественной корреляции	Больше 0,5
Коэффициент асимметрии	А	Степень отклонения фактического распределения случайных наблюдений от нормального (по центру) распределения. Применяется для проверки нормальности распределения	Метод наименьших квадратов может применяться при Л <3
Коэффициент эксцесса	Е	Плосковершинность распределения случайных наблюдений от нормального (по центру) распределения. Применяется для проверки нормальности распределения функции	Меньше 3
Критерий Фишера	F	Математический критерий, характеризующий значимость уравнения регрессии. Применяется для выбора модели	Больше табличного значения, установленного для различных размеров матрицы
Критерий Стьюдента	t	Существенность факторов, входящих в модель. Применяется для выбора модели	Больше 2 (при вероятности, равной 0,95)
Среднеквадратическая ошибка коэффициентов регрессии	Δаi	Точность полученных коэффициентов регрессии. Применяется для оценки коэффициентов регрессии	В два и более раза меньше соответствующего коэффициента регрессии
Ошибка аппроксимации	ΔП	Допуск прогноза или степень несоответствия эмпирической зависимости теоретической. Применяется для оценки адекватности (точности) модели	Меньше (точнее) 15%
Коэффициент эластичности	Эi	Показывает процент изменения функции при изменении соответствующего фактора на 1%. Ранжирование факторов по их значимости	Больше 0,01

Функционально-стоимостный анализ (ФСA) представляет собой метод системного исследования, применяемого в соответствии с назначением изучаемого объекта (процессы, изделия) с целью повышения полезного эффекта, т.е. отдачи на единицу совокупных затрат за жизненный цикл объекта. Важнейшая черта функционально-стоимостного анализа состоит в установлении целесообразности перечня функций, которые должен выполнять проектируемый объект в определенных конкретных условиях, или в проверке необходимости функций уже существующего объекта.

Задачи ФСА:

• достижение оптимального соотношения между полезным эффектом объекта и совокупными затратами за его жизненный цикл;

• нахождение совершенно новых технических решений за счет применения функционального подхода;

• снижение расхода различных видов ресурсов по стадиям жизненного цикла объекта за счет ликвидации или сокращения вспомогательных и вредных (ненужных) функций объекта.

Организация проведения ФСA включает в себя: подготовку к внедрению метода, пропаганду его возможностей для повышения эффективности производства; обучение менеджеров и специалистов основам метода; подготовку специалистов для работы в координационной группе по внедрению ФСА; обеспечение работ по ФСА нормативно-методическими документами; формирование и функционирование рабочих органов ФСА, интегрированных со службами фирмы; создание экономических условий для проведения работ по ФСА и внедрения рекомендаций ФСА на основе их планирования, финансирования и стимулирования.

При проведении ФСА прежде всего устанавливается целесообразность функций, которые должен выполнять проектируемый объект в конкретных условиях, либо целесообразность, достаточность и избыточность функций существующего объекта. Не функции создаются или уточняются для объекта, а, наоборот, выбирается или проектируется объект для выполнения необходимых функций с минимальными затратами за его жизненный цикл. Этапы организации ФСА представлены в табл. 3.10.

Таблица 3.10

Этапы организации функционально-стоимостного анализа

Этапы	Описание
Подготовительный	Выбор объекта анализа. Критерии (или показатели): • удельный вес отдельного изделия (группы изделий) в общей номенклатуре производства по годовой себестоимости; • перспектива выпуска данного изделия (группы изделий) на ближайшие годы; • наличие "узких мест" на разных участках производства, в материально-техническом снабжении, в конструкции изделия или в сфере его эксплуатации. Подбор членов исследовательской рабочей группы (ИРГ) для решения поставленной задачи. Определение сроков, конкретных результатов, которых должна достигнуть группа, порядок взаимодействия с соответствующими службами. Работа на данном этапе считается законченной после издания приказа по предприятию о проведении ФСА. Приказ (распоряжение) должен содержать: объект, цели, сроки проведения ФСА, состав ИРГ, источники финансирования и экономического стимулирования, перечень и порядок представления информации службами предприятия
Информационный	Информационное обеспечение ФСА предусматривает: • подготовку, сбор, систематизацию информации об объекте ФСА и его аналогах; • изучение конструкции объекта и его аналогов, условий его эксплуатации, технологии создания объекта; • построение структурно-элементной модели – "схемы" изделия; • анализ стоимостной информации, определение затрат на изготовление и функционирование объекта и его составных частей, затрат на его ремонт и обслуживание за весь жизненный цикл изделия; • по несущественным объектам – анализ потребностей потребителей и своих возможностей; • дополнение структурно-элементной модели – "схемы" объекта и его составных частей стоимостной информацией;
		• выявление зон наибольшего сосредоточения затрат в исследуемом объекте; • анализ патентной информации и рационализаторских предложений, в том числе ранее отклоненных. Для уяснения состава изделия разрабатывается структурно-элементная модель (далее – структурная модель, схема) путем расчленения изделия на сборочные единицы, детали, конструктивные элементы. Исходной информацией для построения структурной модели являются рабочие чертежи и спецификации на изделие и его сборочные единицы. Для каждой составной части объекта определяются производственные затраты, включающие прямые затраты (материальные – стоимость основных материалов и трудовые – трудоемкость изготовления изделия в форме заработной платы), и затраты, связанные с использованием технологического оборудования, оснастки, инструмента. Данные по производственным затратам должны представляться соответствующими службами предприятия, перечисленными в приказе о проведении ФСА. При отсутствии каких-либо данных по затратам их необходимо спрогнозировать или рассчитать следующим образом: стоимость материалов на основе специфицированных норм расхода материалов и расценок на эти материалы по действующим прейскурантам; стоимость изготовления на основе пооперационных технологических карт и норм времени и расценок на заготовительные, механические и сборочно-сварочные работы; расходы, связанные с использованием оборудования и инструментов с помощью метода нормативной себестоимости, машиночаса и машинокоэффициентов
Аналитический		• оцениваются связанные с осуществлением функций затраты в увязке с соответствующими материальными носителями; • строятся функционально-стоимостная диаграмма, модель объекта; • определяются противоречия между значимостью функций и их стоимостной оценкой; • формулируются задачи совершенствования объекта для последующих этапов ФСА. Целью формулирования всех возможных функций объекта и его составных частей является поиск излишних функций, в которых заложен излишний ресурс
Творческий		На творческом этапе осуществляется выработка предложений по совершенствованию объекта; анализ и предварительный отбор предложений для реализации; систематизация предложений по функциям; формирование вариантов выполнения функций. Целью творческого этапа является нахождение как можно большего количества вариантов технических решений, обеспечивающих ликвидацию бесполезных и вредных функций, совмещение и изменение функций, совершенствование реализации полезных функций объекта
Исследовательский		Основная задача этапа – определение возможности реализации предложенных решений. Перечень основных работ: • разработка эскизов по отобранным вариантам; • экспертиза подготовленных решений; • отбор наиболее рациональных вариантов решений; • создание при необходимости макетов или опытных образцов для проведения испытаний; • проведение испытаний; • окончательный выбор реализуемых решений; • технико-экономическое обоснование решений. По ранее отобранным вариантам осуществляется конструкторская проработка, целью которой является полное представление о предполагаемой конструкции и оценка ее соответствия требованиям технических условий, технологичности, металлоемкости и т.д.
Рекомендательный	Основная задача этапа – определение порядка реализации рекомендаций ФСА. На рекомендательном этапе осуществляются: рассмотрение представленных технических решений на научно- техническом совете предприятия: принятие решения о возможности их реализации; согласование мероприятий по реализации принятых решений. На рассмотрение представляются все варианты решений, отобранные на исследовательском этапе, в виде эскизов с пояснительными записками, в которых указываются их достоинства и недостатки, к каждому решению прилагается расчет экономического эффекта. Все представленные варианты делятся на три группы: 1) решения, не требующие серьезных конструкторских и технологических доработок; 2) решения, для реализации которых требуется проведение каких-либо испытаний и доработки объекта; 3) решения, коренным образом изменяющие конструкцию и технологический процесс изготовления изделия, требующие проведения опытно-конструкторских работ, а также дополнительных капитальных вложений для своего осуществления
Внедренческий	Основная задача этапа – обеспечить безусловное внедрение принятых решений. На этапе внедрения осуществляются: • включение мероприятий по обеспечению внедрения принятых предложений ФСА из плана-графика в стратегию организации, планы задействованных служб и ответственных исполнителей; • контроль выполнения плана-графика; • оценка фактической экономической эффективности внедрения результатов ФСА; • поощрение членов исследовательской рабочей группы и всех участников. Ответственность за своевременное внедрение мероприятий ФСА несет главный менеджер или другое должностное лицо

Анализ чувствительности применяется при принятии решения в области инвестиций. Целью анализа чувствительности является определение степени влияния различных факторов на финансовый результат проекта. В качестве интегральных показателей, характеризующих финансовый результат проекта, используются обычно следующие показатели:

• внутренний коэффициент рентабельности (IRR);

• срок окупаемости проекта (РВР);

• чистая приведенная величина дохода (NPV);

• индекс прибыльности (PI).

Факторы, варьируемые в процессе анализа чувствительности, можно разделить на две основные группы: факторы, влияющие на объем поступлений, и факторы, влияющие на объем затрат.

На рис. 3.8 представлены различные виды изменений в зависимости от факторов.

Рис. 3.8. Виды изменений в зависимости от влияния факторов

В качестве варьируемых факторов принимаются:

• физический объем продаж как следствие емкости рынка;

• доли предприятия на рынке;

• потенциал роста рыночного спроса;

• продажная цена и тенденции ее изменений;

• прямые (переменные) издержки и тенденции их изменений;

• постоянные издержки и тенденции их изменений;

• требуемый объем инвестиций;

• стоимость привлекаемого капитала;

• в отдельных случаях – показатели инфляции.

Этапы анализа чувствительности. Первый этап определяет выделение ключевых параметров проекта (NPV, IRR, FV и т.д.), изменение которых существенно отразится на потоках проекта и влияющих на их значения факторах (выручка, себестоимость, зарплата, налоги и т.д.). На втором этапе проводится расчет ключевых параметров при базовых значениях факторов. Третий этап заключается в последовательном изменении факторов и расчете ключевых параметров при новых условиях. На четвертом этапе проводится проверка чувствительности выбранных параметров при вероятности отклонений первого типа (вероятность того, что фактор изменится, т.е. станет больше, меньше или останется плановым) и второго типа (если фактор все же окажется ниже планового уровня, то с вероятностью 60% отклонение будет не более 10%). Затем определяются наиболее чувствительные к этим изменениям ключевые параметры и факторы, оказывающие самое большое воздействие. И последний этап – сравнение чувствительности проекта по каждому фактору.

Исследование чувствительности показателей эффективности к изменению ставки дисконтирования позволяет определить устойчивость проекта по отношению к колебаниям конъюнктуры финансового рынка и возможным изменениям макроэкономических условий деятельности (рис. 3.9).

Чем шире диапазон параметров, в котором показатели эффективности остаются в пределах приемлемых значений, тем выше запас прочности проекта, тем лучше он защищен от колебаний различных факторов, оказывающих влияние на результаты реализации.

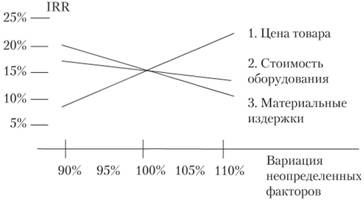
Рис. 3.9. Анализ чувствительности в графиках (пример)

Анализ чувствительности проводят как при планировании, так и при анализе инвестиционных проектов. Полученные в результате проведенного анализа чувствительности данные служат основой для оценки финансового риска проекта, а также помогают разработать стратегию наиболее безопасного и эффективного пути его реализации.