Компьютерные технологии решения экономических задач
В процессе своей профессиональной деятельности (образовательной, научной, технологической, художественной) мы используем различные модели для описания объектов и процессов окружающего мира.
Модель – это искусственно созданный образ реального объекта, явления или процесса в целях изучения его существенных признаков и свойств. Моделирование – это метод познания, заключающийся в создании и исследовании моделей. Различают два больших класса моделей – предметные и информационные.
Предметные модели отражают физические, геометрические и другие свойства объектов в материальной форме (прототипы зданий и сооружений, муляжи, глобус и т.д.).
Информационная модель – описание объекта, явления или процесса с помощью знаковых форм, т.е. система знаний, содержащаяся в совокупности информации, характеризующей существенные свойства и состояния объекта, процесса, явления, а также взаимосвязь между их элементами.
Развитие компьютерных технологий позволило для создания и исследования информационной модели использовать современные компьютерные технологии, в результате чего в науке появился термин "компьютерное моделирование". Компьютерное моделирование – метод представления системы знаний об объекте и его взаимосвязях с помощью компьютерной модели. В настоящее время компьютерное моделирование в научных и практических исследованиях является одним из основных методов познания. Использование компьютерного моделирования позволяет решать масштабные научные и экономические задачи. Объектом компьютерного моделирования могут выступать экономическая деятельность фирмы или банка, промышленное предприятие, информационно-вычислительная сеть и т.д.
Объекты, изучаемые экономической наукой, в большинстве случаев представляют собой некую систему сгруппированных подсистем, которая формируется для решения определенных целей социально-экономических процессов. Экономическая система – это совокупность взаимосвязанных подсистем с соответствующими функциями, выполнение которых в определенной последовательности приводит к реализации экономической задачи.
Поскольку экономические задачи, как правило, достаточно сложны по своей структуре, содержат большой объем информации и т.д., для их решения применяют компьютерное моделирование, в рамках которого на основе применения алгоритмов создаются компьютерные и математические модели экономической системы с дальнейшей компьютерной реализацией.
Операции с массивами и матрицами
Векторы и матрицы в электронной таблице Excel хранятся в виде массивов. Массив представляет собой набор однотипных данных, который хранится в электронной таблице в виде диапазона ячеек. Электронная таблица Excel позволяет решать задачи с использованием массивов различной размерности: одномерные, двумерные и трехмерные. Одномерные и двумерные массивы хранятся на одном листе рабочей книги, а трехмерный массив размещается в одноименных областях смежных листов рабочей книги.
С массивами, содержащими числовые данные, можно выполнять различные арифметические операции, в которых участвуют:
• элементы массива и число, например почленное умножение;
• элементы двумерного массива и элементы одномерного массива (вектора), например почленно-построчное умножение;
• массивы различной размерности и т.д.
Для выполнения арифметических операций (сложение, вычитание, умножение, деление и т.д.) над элементами массива требуется:
• выделить область для размещения результата в соответствии с условием задачи;
• в строку формул после знака "равно" вести соответствующее арифметическое выражение;
• закончить ввод формулы комбинацией клавиш Ctrl + Shift + Enter, означающей, что результат выполнения данной формулы располагается в диапазоне ячеек.
Вычисление суммы векторов. Для вычисления суммы векторов необходимо последовательно выполнить следующие операции:
• в диапазоны ячеек одинаковой размерности ввести значения числовых элементов каждого вектора;
• выделить диапазон ячеек для вычисляемого результата такой же размерности, что и исходные векторы;
• ввести в выделенный диапазон формулу сложения диапазонов: = АдресВектора 1 + Адрес_Вектора_2;
• нажать комбинацию клавиш Ctrl + Shift + Enter (рис. 9.5).
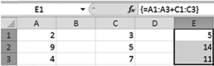
Рис. 9.5. Вычисление суммы векторов
Умножение массива на число. Для умножения массива на число в электронной таблице необходимо выполнить следующие операции:
• в диапазоны ячеек ввести значения числовых элементов массива:
• выделить диапазон ячеек для вычисляемого результата такой же размерности, что и исходный массив;
• ввести в выделенный диапазон формулу умножения диапазона на число: = АдресВектора * 3;
• нажать комбинацию клавиш Ctrl + Shift + Enter (рис. 9.6).

Рис. 9.6. Умножение массива на число
Скалярное произведение векторов. Сумма произведений соответствующих координат векторов называется скалярным произведением векторов и вычисляется с помощью формулы a•b = а1•b1 +а2•b2 + ... + аn•bn.
Для вычисления скалярного произведения векторов необходимо:
• в диапазоны ячеек одинаковой размерности ввести значения числовых элементов каждого вектора;
• выделить диапазон ячеек для вычисляемого результата такой же размерности, что и исходные диапазоны;
• ввести в выделенный диапазон формулу перемножения диапазонов: = Адрес_Вектора_1 * Адрес_Вектора_2;
• нажать комбинацию клавиш Ctrl + Shift + Enter;
• просуммировать содержимое ячеек диапазона, в котором размещен результат умножения диапазонов.
Для вычисления скалярного произведения в Excel также используется функция СУММПРОИЗВ.
Умножение матрицы на число. Массив, значения элементов которого записаны в двумерной области, может представлять собой двумерную матрицу. Умножение двумерной матрицы на число аналогично операции умножения массива на число, описанной выше.
Сложение и вычитание матриц. Суммировать матрицы (векторы) и находить их разность можно только в том случае, если они имеют одинаковую размерность. Матрицы (векторы) складываются (вычитаются) поэлементно.
Например, требуется найти матрицу С, полученную в результате суммирования матриц А и В. Для этого необходимо выполнить следующие действия:
• выделить диапазон, где будут размещаться элементы матрицы С, полученной в результате суммирования матриц А и В;
• в выделенный диапазон ввести формулу: = Адрес_ Матрицы_1 + Адрес_Матрицы_2;
• нажать комбинацию клавиш Ctrl + Shift + Enter (рис. 9.7).

Рис. 9.7. Сложение матриц
Аналогичным образом вычисляются разность, скалярное произведение и деление матриц.
Произведение матриц. Для того чтобы можно было вычислить произведение матриц, должно выполняться следующее условие: количество столбцов первой матрицы A должно быть равным количеству строк второй матрицы В. Если размерность матрицы А т × п, а матрицы В п × r, то в результате произведения получится матрица С с размерностью m × r, где каждый ее элемент будет равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В:

где i = 1, 2, ..., m; j= 1, 2, ..., r.
Произведение матриц в электронной таблице MS Excel осуществляется с помощью встроенной функции МУМНОЖ с синтаксисом МУМНОЖ(Массив1; Массив2), где Массив1 – адрес диапазона, в котором находятся элементы первой матрицы, а Массив2 – адрес диапазона, в котором находятся элементы второй матрицы (рис. 9.8).

Рис. 9.8. Вычисление произведения матриц
Нахождение обратной матрицы. Чтобы найти матрицу А-1, обратную для матрицы А, необходимо выполнить следующие действия:
• выделить диапазон, где будут размещаться элементы обратной матрицы А-1, размерность которой совпадает с размерностью А;
• в выделенный диапазон ввести формулу: = МОБР(А).
Транспонирование матрицы. Транспонирование матрицы – процесс перестановки элементов матрицы, когда элементы строк матрицы становятся элементами ее столбцов и наоборот, т.е. если матрица имела размерность т × п до транспонирования, полученная матрица будет иметь размерность n × m. Excel существует функция ТРЛНСП, позволяющая транспонировать матрицы.
Рассмотрим операцию транспонирования матрицы. Требуется транспонировать матрицу А размерности т × п, для этого необходимо выполнить следующие действия:
• выделить диапазон с размерность п × т;
• в выделенный диапазон ввести формулу ТРАНСП(А).