Задачи формирования портфелей ценных бумаг

Портфель ценных бумаг - это совокупность различных инвестиционных инструментов, которые собраны воедино для достижения конкретной инвестиционной цели вкладчика.

В портфель могут входить бумаги только одного типа, например, акции или облигации, или различные инвестиционные ценности, такие как акции, облигации, депозитные и сберегательные сертификаты и т.д.

Портфельный менеджмент, т.е. формирование инвестиционного портфеля ценных бумаг, берет свое начало примерно с тех времен, когда появились сами ценные бумаги. Методология же инвестиционного менеджмента начала складываться в 1920-е гг. с появлением понятия "истинной" цены (fair price) акции. Задача инвестора состояла в том, чтобы приобрести недооцененные акции, чья рыночная цена на момент покупки ниже истинной, и избавиться от переоцененных бумаг и тем самым получить в перспективе максимальную прибыль. Эта цель не менее актуальна и сейчас.

Начало современной теории финансового портфеля было заложено в статье Гарри Марковица "Выбор портфеля" (1952). В ней предложена математическая модель формирования оптимального портфеля ценных бумаг и приведены методы построения таких портфелей при определенных условиях. С вычислительной точки зрения получающаяся оптимизационная задача относится к классу задач квадратической оптимизации при линейных ограничениях. К настоящему времени вместе с задачами линейного программирования это один из наиболее изученных классов оптимизационных задач, для которых разработано большое число достаточно эффективных алгоритмов.

Затем в работах В. Шарпа (1964) и Дж. Литнера (1965), приводились понятия систематического (рыночного) и несистематического рисков ценной бумаги.

Риск (в литературе также встречается термин общий риск) ценной бумаги есть неопределенность ее дохода в конце периода инвестирования.

Риск измеряется дисперсией доходности ценной бумаги за фиксированный интервал времени, например, месяц, квартал, год и т.д. Данное определение риска считается наиболее распространенным, хотя существуют и другие.

Главная цель в формировании портфеля состоит в достижении оптимального сочетания между риском и доходом для инвестора, т.е. соответствующий набор инвестиционных инструментов призван снизить до минимума риск его потерь и одновременно максимизировать его доход.

Для получения количественных характеристик инвестиционного портфеля могут использоваться следующие показатели:

1) доходность портфеля ценных бумаг тр. Данный параметр рассчитывается как взвешенная средняя из ожидаемых доходов по каждому из компонентов

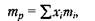
где х-, - доли инвестиций, помещенных в каждый из видов активов (эти доли называют портфельными весами) ХТ = = (х^ х2, х"); т-, - ожидаемая ставка дохода по каждому виду активов;

2) риск портфеля а" - стандартное отклонение ставок дохода по портфелю. Представляет собой квадратный корень из дисперсии портфельного дохода (дисперсию доходности портфеля называют его вариацией V,,), которая определяется по формуле

где Соу - ковариационная матрица "-го порядка.

Ковариация - это статистическая мера взаимодействия двух случайных переменных, таких, например, как доходности двух ценных бумаг.

Положительное значение ковариации показывает, что доходности этих ценных бумаг имеют тенденцию изменяться в одну сторону. Ковариация между двумя акциями х и у рассчитывается следующим образом:

Содержательно интерпретировать численное значение ковариации достаточно сложно, поэтому очень часто для измерения силы связи между двумя переменными используется другая статистическая характеристика, называемая коэффициентом корреляции. Этот коэффициент позволяет стандартизировать ковариацию путем деления ее на произведение соответствующих средних квадратических отклонений и привести величины к сопоставимому виду. Коэффициент корреляции между двумя переменными I и) рассчитывается следующим образом:

Знак коэффициента корреляции совпадает со знаком ковариации, поэтому положительная его величина означает однонаправленное изменение переменных, а отрицательная - их изменение в противоположных направлениях. Если значение Гц близко к нулю, связь между переменными слабая. Кроме того, процедура стандартизации приводит к тому, что коэффициент корреляции принадлежит интервалу от -1,0 до +1,0. Отметим также, что формула (30.11) может использоваться для расчета ковариации, которая может быть выражена как произведение коэффициента корреляции Гц и двух стандартных отклонений:

где о,- - стандартное отклонение дохода по г'-му активу; Гу - коэффициент корреляции доходов между г'-м и_/-м активами.

Рис. 30.8. Доходность двух ценных бумаг:

а, 6 - соответственно полная положительная и отрицательная корреляции между доходностями; в - некоррелированные доходности

Наличие совершенной положительной корреляции (рис. 30.8, а) наблюдается, например, при приобретении двух видов обычных акций одной корпорации, выпущенных на одинаковых условиях. Это означает, что когда одна из двух ценных бумаг имеет относительно высокую доходность, тогда и другая ценная бумага имеет относительно высокую доходность. Стандартное отклонение ставок дохода по портфелю в этом случае рассчитывается как средневзвешенная из стандартных отклонений доходов, входящих в состав портфеля активов.

При наличии совершенной отрицательной корреляции (рис. 30.8, б), когда при уменьшении дохода по одной акции на один пункт происходит увеличение на один пункт по другой, инвестор получает возможность уменьшить стандартное отклонение дохода по этим двум активам вместе до нуля, т.е. свести риск к минимуму.

Рассмотрим портфель, состоящий из двух видов ценных бумаг: акций с ожидаемой доходностью 12% и облигаций, доход по которым составляет 5,1%. Стандартное отклонение акций 21,2%, облигаций - 8,3%.

Варьируя портфельные веса включенных в состав портфеля активов, можно добиться оптимального портфеля, с точки зрения применяемого типа активов. Результат такого варьирования может быть представлен в табл. 30.6.

Портфель "0" состоит только из облигаций, тогда как портфель "21" только из акций. 11ортфель, состоящий только из облигаций, имеет ожидаемый доход 5,1%, а стандартное отклонение портфельного дохода - 8,3%. Портфель, состоящий только из акций, имеет ожидаемый доход в 12%, а стандартное отклонение - 21,2%. Портфель, состоящий на 60% из акций и на 40% из облигаций, будет иметь ожида

Таблица 30.6. Ожидаемый доход и стандартное отклонение портфеля

емый доход в 9,24%, стандартное отклонение дохода по такому портфелю составит 13,71%, если корреляция между изменениями доходов по облигациям и акциям равна (г = 0,18). Если изменения доходов по облигациям и акциям характеризуются совершенной положительной корреляцией (г= 1,00), то тогда ожидаемый доход останется прежним, а стандартное отклонение будет включать 60% разности между более высоким стандартным отклонением дохода по акциям и стандартным отклонением дохода но облигациям.

В связи с тем, что корреляция между изменениями доходов по облигациям и по акциям не является совершенной, меньшими оказываются и значения стандартного отклонения портфельного дохода. Если представленные облигации могут служить идеальным средством хеджирования вложений в акции или, другими словами, корреляция между изменениями доходов по облигациям и акциям оказывается совершенной и при этом отрицательной (г = -1,00), то стандартное отклонение портфельного дохода будет равно только 9,4%. В этом случае можно сформировать портфель, состоящий на 28% из вложений в акции и на 72% - в облигации (портфель "6"), у которого стандартное отклонение портфельного дохода практически равняется нулю. Это означает, что с вероятностью, равной единице, указанный портфель будет иметь совокупный доход, составляющий 7,03%.

Представим графически зависимость величины стандартного отклонения от ожидаемого дохода (рис. 30.9) при различных коэффициентах корреляции.

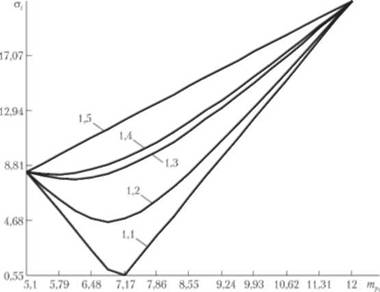
Рис. 30.9. Зависимость стандартного отклонения дохода от ожидаемого