Классификация степеней неопределенности социально-экономических систем и методов принятия решений

Учитывая фактор неопределенности, некоторые авторы делят модели на детерминированные и стохастические (вероятностные). Параметр классификации, а следовательно, и предлагаемое ими деление моделей с нашей точки зрения является неточным, поскольку параметром классификации следует рассматривать степень неопределенности объекта в модели, и тогда в соответствии с этим критерием экономико-математические модели делятся как минимум на три класса.

1. Детерминированные, если ошибка моделирования, характеризующая величину отклонения фактического значения выходной переменной от ее расчетного идеального значения, равна нулю (ε = 0).

2. Стохастические (вероятностные), если ошибка моделирования не равна нулю (е * 0), но описывается известными вероятностными законами.

3. Нечеткие, если присутствуют объект и субъект моделирования, но они неопределённы. В моделях такого типа используется теория нечетких множеств.

Таким образом, этот вопрос нуждается в дополнительном исследовании. Рассмотрим два типичных, характерных для последующего изложения примера.

Задача 5.6. Детерминированная система принятия решений. Перед службой по труду и занятости населения региона поставлена задача выбора учебных заведений, которые наилучшим образом и с наименьшими затратами окажут услуги по организации процесса переподготовки кадров по тем или иным направлениям. Решение данного вопроса легко реализуемо с использованием формальных методов теории линейного программирования (ТЛП). Высшие учебные заведения в данной задаче рассматриваются авторами цитируемого источника как составные элементы единой системы образования, нацеленной на получение наилучшего результата.

Пусть в этой системе есть п участников (вузов), способных решить поставленную задачу, заключающуюся в переподготовке определенных групп людей. Необходимо распределить между ними т работ (учебных курсов, дисциплин, образовательных программ).

На первом этапе исследования идентифицируется матрица возможностей членов образовательной системы по реализации указанных работ (табл. 5.4).

Таблица 5.4

Стоимость оказания образовательных услуг в вузах по направлениям (тыс. руб.)

Дисциплины / Вузы	А	Б	В	Г	Д	Е	Объем возможных работ
ЮФУ	130	115	90	100	80	85	3
РГУПС	110	120	70	95	50	60	2
РГЭУ	120	130	90	110	70	90	2
СКАГС	140	120	90	85	90	80	1
Количество проводимых курсов	1	1	1	1	1	1	8 / 6

Исходя из табл. 5.4, обозначим: aij – стоимость выполнения j-й работы i-м вузом; cj – количество курсов, которые может провести i-й вуз. В этой постановке предполагается, что качество оказываемых услуг участников образовательного процесса одинаково (соответствует образовательному стандарту).

Обозначив через xij факт назначения проведения j-го курса i-му вузу, получаем следующую систему:

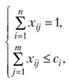(5.11)

при этом хij= 0, если дисциплина j не поручается вузу i, и хij = 1, если указанная работа поручена соответствующему учебному заведению. Первое уравнение отражает тот факт, что задание поручается только одному участнику, второе описывает установленные выше возможности высших заведений.

Целевая функция задачи имеет следующий вид:

(5.12)

Это требование означает, что суммарные затраты на проведение всего комплекса дисциплин силами учебных заведений за финансовые средства органов занятости населения должны быть минимальными.

Данная задача легко решается стандартными программными средствами ТЛП.

Авторы цитируемой работы дают решение данной задачи на примере г. Ростова-на-Дону . Выделено четыре вуза, готовых осуществлять профессиональную переподготовку безработных, направляемых службой занятости:

• Южный федеральный университет (ЮФУ);

• Ростовский государственный университет путей сообщения (РГУПС);

• Ростовский государственный экономический университет (РГЭУ);

• Северокавказская академия государственной службы (СКАГС).

Задача состоит в переподготовке кадров, обратившихся за помощью в службу занятости региона, по следующим шести направлениям (т = 6):

• малый и средний бизнес (А);

• бухгалтерский учет на предприятии (Б);

• бюджетирование компании (В);

• налогообложение на предприятии (Г);

• основы предпринимательской деятельности (Д);

• ведение бухгалтерского учета индивидуальным предпринимателем (Е).

Матрица возможностей участников системы образования по реализации указанных работ представлена в табл. 5.4.

Для сохранения конкуренции на рынке образовательных услуг экспертно было определено максимальное количество курсов, которые может провести каждый из вузов (столбец "Объем возможных работ" в табл. 5.4). Это значения сi, в общей постановке задачи.

Задача заключается в составлении плана работ вузов таким образом, чтобы все курсы были проведены, суммарная стоимость их проведения была бы минимальной, а эффективность мероприятий, направленных на переобучение, была высокой.

Решение данной задачи легко осуществимо в стандартных программных продуктах Excel с использованием настройки "Поиск решения", и оно отражено в табл. 5.5.

Таблица 5.5

Решение задачи переобучения с использованием программного продукта MS Excel "Поиск решения"

Дисциплины / Вузы	А	Б	В	Г	Д	Е	Объем оказываемых услуг
ЮФУ	0	1	0	0	0	1	2
РГУПС	1	0	1	0	0	0	2
РГЭУ	0	0	0	0	1	0	1
СКАГС	0	0	0	1	0	0	1
Количество проводимых курсов	1	1	1	1	1	1	6 / 6

Из табл. 5.5 следует, что ЮФУ целесообразно поручить обучение по специальностям "Бухгалтерский учет на предприятии" и "Ведение бухгалтерского учета индивидуальным предпринимателем". Для РГУПС целесообразны курсы "Малый и средний бизнес" и "Бюджетирование компании". РГЭУ и СКАГС реализуют по одной программе – "Основы предпринимательской деятельности" и "Налогообложение на предприятии" соответственно.

Расчеты показали, что минимальная стоимость оказания образовательных услуг с учетом введенных ограничений составляет 535 тыс. руб.

Проанализируем пример с точки зрения введенных в предыдущем параграфе параметров системы управления. В данном примере структура f образовательной системы (объекта исследования) определяется соотношениями (5.11) и табл. 5.4, выход системы и критерий функционирования задаются формулой (5.12). Управляющие воздействия заданы табл. 5.5. Шумы (показатель W) отсутствуют – все данные известны точно.

Задача 5.7. Нечеткая система принятия решений. В Центре инновационного развития холдинга ожидают своего решения четыре перспективных для разработки проекта: В1, В2, В3, В4 различающиеся сложностью подготовки, потребностями в кадрах, площадях, финансах, материалах и другими факторами. Оценить эти факторы с достаточной точностью не удается. Нет данных и опыта проведения аналогичных проектов. Эксперты должны принять решение о порядке внедрения проектов только на основании своей интуиции. При этом они должны учесть, по крайней мере, три критерия Ji, которые отражают следующие важные показатели реализации проектов:

• сроки исполнения проекта J1;

• рентабельность J2;

• затраты на внедрение J3.

Аналитические зависимости Ji от факторов системы и среды априори неизвестны, статистики для их построения (как в задачах 5.2-5.4) также нет. На основании сказанного можно составить таблицу, аналогичную табл. 5.6. Порядок заполнения такой таблицы и механизм оперирования ею для принятия решений рассмотрен далее.

Таблица 5.6

Экспертные исходные данные для выбора проекта

	B1	В2	В3	В4
J1
J2
J3

Поля таблицы заполняет эксперт, ориентируясь на свой личный опыт и интуицию.

Приведенные выше примеры в определенном смысле диаметрально противоположны. Если в задаче 5.6 известны элементы X, Y, f, J, ошибки их задания W пренебрежимо малы и можно считать W = 0, то во втором – ни один из элементов процедуры принятия решений математически не формализован. Большинство реальных задач принятия решений в экономике по степени информированности занимает некоторое промежуточное положение между полной определенностью и полной неопределенностью.

В зависимости от полноты исходной информации и конкретных свойств исследуемого объекта для расчета искомых управлений применяется тот или иной математический аппарат. В табл. 5.7 приведена краткая классификация некоторых возможных степеней неопределенности через указание характеристик исходных данных и соответствующие методы принятия решений. Указанные степени условны и не отражают всего разнообразия возможных практических ситуаций, а служат лишь для иллюстрации рассматриваемого вопроса.

Первая степень неопределенности предполагает, что функционал J и структура f известны. Они так же, как и X и Y, не искажены шумом W. В качестве иллюстрации этой степени неопределенности см. задачи 5.1 и 5.6. В этом случае используются хорошо разработанные оптимизационные методы линейного, нелинейного, целочисленного, динамического программирования, прямые вариационные методы (наискорейшего спуска, градиентные), а также методы, основанные на принципе максимума Понтрягина (см. приложение 1).

Таблица 5.7

Классификация неопределенности и методов принятия решений

Степени неопределенности	Характеристики исходных данных				Методы принятия решений
	детерминированные	статистические	экспериментальные	заданные на основе интуиции и опыта, гипотетические
1	J, f, x, y W = 0				Вариационные, принцип максимума Понтрягина, линейное, нелинейное программирование и т.д.
2	J, f	x, y, w			Теория вероятностей, математическая статистика, статистические методы теории распознавания образов и т.д.
3	J, f		x, y, w		Предыдущие и специальные методы, использующие регуляризующие процедуры
4			J, f, x, y, w		Эвристическая самоорганизация классических процедур принятия решений, обучение, персептрон Розен-блата, машина Гамба и т.д.
5				J, f, x, y, w	Теория нечетких множеств

С помощью методов, приведенных в табл. 5.7, решаются различные задачи распределения ресурсов, транспортных потоков, планирования производства, замены оборудования и др. При более подробном рассмотрении этих задач легко заметить, что практически все указанные ограничения в них не выполняются. Тем не менее детерминистские модели находят широкое применение и в ряде случаев позволяют получить хорошие решения. Весь вопрос заключается в том, чтобы в каждом случае очертить круг задач и выявить предпосылки применения этих методов.

Следующим шагом в развитии теории принятия решений является учет и анализ вероятностных характеристик в оптимизационных моделях. При этом любая неопределенность будет рассматриваться нами как совокупность неполных предсказаний, характеризуемая некоторым распределением вероятностей различных возможных событий (или исходов). Обычно вероятностные модели представляют собой усложненные варианты детерминистских моделей, хотя существует ряд методов, отражающий конкретную специфику этого уровня неопределенности исходных данных (принятие решений по минимуму риска). Переход к вероятностным моделям снимает ряд ограничений и этим расширяет круг решаемых задач. Вместе с тем для многих задач не удается дать удовлетворительного обоснования необходимых законов распределения, и они принимаются на основе интуиции исследователя или из соображений упрощения алгоритмов принятия решений. Это часто приводит к неверным выводам, искаженным результатам управления. Кроме того, вероятностные алгоритмы значительно сложнее с точки зрения вычислительной.

В качестве примеров этого уровня неопределенности среди ранее рассмотренных в параграфе 5.1 можно указать:

• задачу 5.2, исследующую затраты, прибыль и себестоимость фирмы, при предположениях, что структура зависимости (5.4) (квадратичная функция затрат) известна априори и не требует включения механизмов самоорганизации для ее идентификации, а также, что в процессе счета вычислительных проблем не возникает;

• задачу 5.3, где также следует предполагать, что принятая структура погодных условий (два варианта погоды) вполне адекватна по точности описания существующего разнообразия погодных условий, а изменения погоды стационарны, т.е. вероятности наступления влажной или сухой погоды неизменны в прошлом и будущем;

• задачу 5.4, посвященную классификации фирм. Но и в этой задаче есть ряд жестких требований, которые должны быть выполнены: классов – два, мера близости – евклидова, метод эталона отражает суть проводимой классификации (а не метод ближайшего представителя или метод потенциалов, например).

В условиях ограниченного набора исходных данных и отсутствия предпосылок, предполагая тот или иной закон распределения X, Y, W (такие данные в табл. 5.7 отмечены как экспериментальные), при априори известных J и f статистические алгоритмы принятия решений можно усовершенствовать, используя регуляризующие процедуры.

Следующий, более высокий уровень неопределенности возникает, если в исследуемом объекте нет достаточной априорной информации o J и f для организации устойчивых регуляризованных алгоритмов. В этом случае возникают дополнительные трудности при нахождении структуры и показателей эффективности задачи. Эти вопросы решаются на основе методов самоорганизации. Прокомментировать этот уровень неопределенности можно теми же примерами из предыдущего параграфа, но при этом следует задать вопрос, а выполняются ли все высказанные условия и возможно ли выполнить все необходимые процедуры. Достаточны ли они для решения задачи? Например:

• в задаче 5.3 определить структуру уравнения 5.4, оптимальную по некоторому критерию;

• в задачах 5.3 и 5.4 выявить необходимое число классов (погодных условий, типов фирм);

• в задаче 5.4 найти наилучший метод классификации и критерий классификации.

Последняя степень неопределенности, выделенная в табл. 5.7, относит нас к информации, известной из опыта и интуиции исследователя. Это также гипотетические и директивные (установленные заказчиком, желаемые) данные. Их отличает наибольшая неопределенность и противоречивость, что приводит к плохо формализуемой, многокритериальной задаче (см. задачу 5.7). Необходимым, а иногда и единственно возможным средством формализации задачи принятия решений является в этом случае теория нечетких множеств.

Следует еще раз отметить условность табл. 5.7. Она заключается в следующем.

1. Избраны в качестве классификационных признаков наиболее типичные элементы задачи принятия решений J, f, х, и, w. В конкретных условиях они могут частично отсутствовать, список их может быть расширен или интерпретирован иначе.

2. Предполагается наличие четкой границы между выделенными характеристиками исходных данных (детерминированные, статистические, экспериментальные, гипотетические). Классификация характеристик может быть иной.

3. Рассмотрена ограниченная комбинация элементов J, f, х, и, w и соответствующих характеристик.

Как следует из приведенного выше анализа, СЭС характеризуются следующими свойствами:

• нестационарностью процессов, проявляемой как в пространстве, так и во времени;

• неоднородностью природных условий функционирования, что требует работы управляющих систем в широком диапазоне свойств;

• наличием неизвестных и трудно учитываемых факторов;

• низкой достоверностью получаемой статистической информации вследствие высокой зашумленности данных и сочетанного воздействия трех вышеперечисленных свойств;

• наличием экспертной и интуитивной информации об объекте и системе управления им, слабо формализуемой и потому неэффективно используемой;

• дефицитом времени на принятие решений часто в условиях высокой интенсивности управляемых социально-экономических процессов.

Указанные особенности обусловили необходимость постоянной модернизации (совершенствования) уже действующих систем управления экономическими процессами и объектами.