Классификация основных видов статистических графиков
Для графического представления статистических данных используют самые разнообразные виды графиков (рис. 4.2,4.3). Их можно классифицировать по разным признакам: характеру графического образа, способу построения и назначению (содержанию).
По характеру графического образа различают графики объемные, линейные и плоскостные (рис. 4.2).
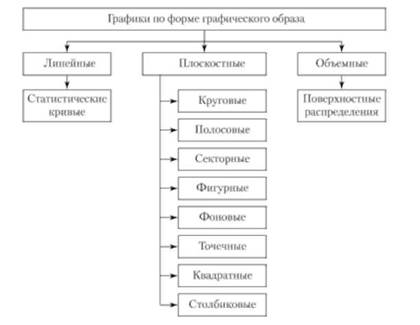
Рис. 4.2. Классификация статистических графиков по форме графического образа
По способу построения графики можно подразделить на диаграммы и статистические карты (рис. 4.3).
Диаграмма представляет собой чертеж, показывающий соотношение статистических данных с помощью разнообразных геометрических и изобразительных средств.
Статистические карты предназначены для графического изображения одноименных показателей, относящихся к разным территориям. Для этого в основу изображения берется географическая карта. Изображение па карте статистических данных называется картограммой или картодиаграммой.
По содержанию или назначению можно выделить графики сравнения в пространстве, относительных величин (структуры, динамики и т.п.), вариационных рядов,
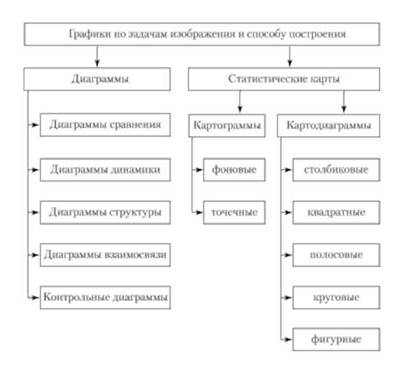
Рис. 4.3. Классификация статистических графиков но способу построения и содержанию изображаемых данных
взаимосвязанных показателей и размещения по территории (статистические карты). В целом классификация графиков по задачам изображения явления представлена на рис. 4.3.
Диаграммы сравнения
Различные виды диаграмм применяют для сравнения одноименных статистических данных, характеризующих разные территории или объекты. Наиболее распространенным видом таких диаграмм являются столбиковые диаграммы. Они представляют собой график, в котором различные величины изображены расположенными в высоту прямоугольниками (столбиками) одинаковой или разной высоты. Столбиковые диаграммы используют для сравнения некоторых объектов во времени.
Построение такого рода диаграмм требует только одной вертикальной масштабной шкалы, которая определяет высоту каждого столбика.
Масштабная шкала должна начинаться с нуля, быть непрерывной, на ней записывают лишь круглые или округленные значения.
Столбики должны быть расположены на одинаковом друг от друга расстоянии или вплотную. Ширина столбиков берется произвольной. На шкале должна быть указана единица измерения.
Масштаб нужно рассчитать так, чтобы максимальное число отразилось па графике.
Пример. Требуется изобразить с помощью столбиковой диаграммы данные о движении численности работников организаций в экономике региона (цифры условные): в 2010 г. численность работников составила 2822 тыс. человек; в 2009 г. — 2398 тыс.; в 2008 г. - 2406 тыс.; в 2007 г. - 2218 тыс. Примем масштаб: 500 тыс. человек соответствует 1 см. Тогда высота первого столбика (численность работников в 2007 г.) будет равна 4,4 см (1 см = 2218/500); высота второго (в 2008 г.) — 4,8 см; высота третьего (в 2009 г.) — 4,79 см; высота четвертого (в 2010 г.) — 5,6 см. Наглядность данной диаграммы достигается сравнением высоты столбиков (рис. 4.4).
С помощью столбиковой диаграммы показана структура посевных площадей фермерских хозяйств N-й области РФ за 2010 г. (цифры условные) (рис. 4.5). На этой диаграмме столбики располагаются вплотную но группам объектов в пространстве.
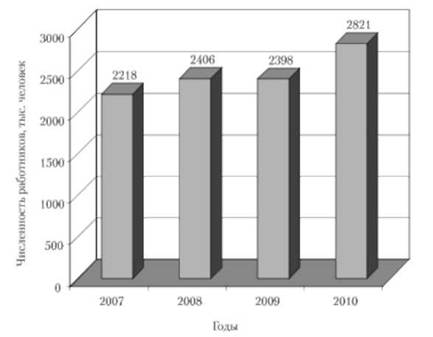
Рис. 4.4. Динамика движения численности работников организаций в экономике за период 2007—2010 гг.
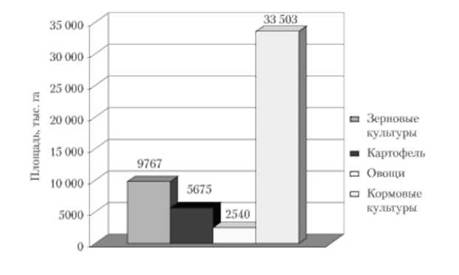
Рис. 4.5. Структура посевных площадей фермерских хозяйств в N-й области РФ в 2010 г.
Если прямоугольники, изображающие показатели, расположить не по вертикали, а по горизонтали, то диаграмма получит название ленточной, или полосовой.
В качестве примера приведем полосовую диаграмму сравнения, характеризующую данные о перевозке грузов транспортом общего пользования в ,¥-м регионе за 2007—2010 гг. (рис. 4.6).
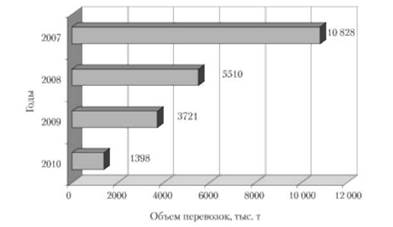
Рис. 4.6. Динамика перевозки грузов транспортом общего пользования в N-м регионе за период 2007—2010 гг.
Иногда разница между наименьшими и наибольшими значениями сравниваемых данных настолько велика, что установление подходящего масштаба для столбиков ил: полос оказывается затруднительным. 15 этих случаях вместо столбиковой (полосовой) диаграммы целесообразно применить плоскостную (двухмерную) диаграмму — квадратную или круговую. Принцип построения этих диаграмм заключается в том, что величины сравниваемых данных изображаются площадями квадратов или кругов. При этом площади квадратов (кругов) должны быть пропорциональны величинам изображаемых явлений, т.е. стороны квадратов или радиусов кругов должны быть пропорциональны корням квадратным из величин изображаемых статистических данных.
Творог..............................................11
Сметана...........................................16
Молоко............................................19
Для построения квадратной диаграммы сначала извлечем квадратные корни из чисел: л/1б = 4; -Лэ = 4,36. Затем установим масштаб, например, примем 1 см = 1,5 млн руб. Тогда сторона одного квадрата составит 2,2 см (3,32 : 1,5); второго — 2,7 см (4 : 1,5); третьего — 2,9 см (4.36 : 1,5). Далее строим квадраты.
Для правильного построения диаграммы квадраты необходимо расположить на одинаковом расстоянии друг от друга, а в каждой фигурке указать числовое значение, которое она изображает, не приводя масштаба измерения (рис. 4.7).
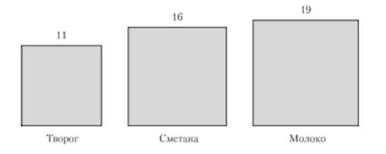
Рис. 4.7. Реализация молочных продуктов фермерскими хозяйствами в одном из регионов за 2010 г., млн руб.
Круговую диаграмму строят аналогично квадратной с той разницей, что находят величину радиуса для каждого круга.
Пример. По данным, приведенным в табл. 4.1, требуется построить круговые диаграммы.
Таблица 4.1/ Данные о числе лиц, потерпевших от преступных посягательств за 2010 г. в одном из регионов
|
Категория граждан |
Численность, тыс. чел. |
|
Несовершеннолетние |
161,6 |
|
Женщины |
1071,8 |
|
Мужчины |
1441,7 |
Чтобы вычислить масштаб, необходимо извлечь корень квадратный из следующих величин: 7161,6 = 12,7; 7Ю71,8 = 32,7; л/1441,7 =38.
Примем 1 см = 6,35 тыс. человек, тогда радиус первого круга будет равен 2,0 см (12,7 : 6,35); второго — 5,2 см: третьего — 5,98 см (рис. 4.8).
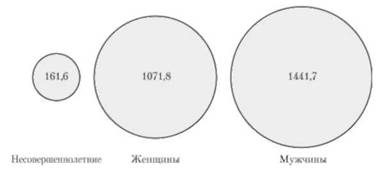
Рис. 4.8. Число лиц, потерпевших от преступных посягательств за 2010 г. в одном из регионов, тыс. человек
Диаграммы, предназначенные для популяризации, иногда строят в виде стандартных фигур-рисунков, характерных для изображаемых статистических данных, что делает диаграмму более выразительной, привлекает к пей внимание. Такие диаграммы называют фигурными или изобразительными. Каждая фигура имеет одинаковый размер и принимается за определенную величину изображаемых статистических данных (рис. 4.9).
Пример. Изобразим динамику производства зерна п регионе за 2007—2010 гг. с помощью диаграммы фигур-знаков. Условно примем один рисунок за 4000 тыс. т. Тогда производство зерна в 2007 г. в размере 9687 тыс. т должно быть изображено в количестве 2,4 рисунка; в 2008 г. в размере 13 623 тыс. т — 3,4 рисунка; в 2009 г. в размере 14 306 тыс. т — 3,6 рисунка; в 2010 г. в размере 15 715 тыс. т — 3,9 рисунка (см. рис. 4.9).

Рис. 4.9. Динамика производства зерна в регионе за период 2007—2010 гг. (цифры условные)
Для графического изображения трех взаимосвязанных показателей, один из которых равен произведению двух других, российский статистик проф. В. Е. Варзар предложил использовать прямоугольную диаграмму, названную им "статистическим знаком". В настоящее время такие диаграммы часто называют знаком Варзара.
Диаграмму строят в виде прямоугольника, основание которого пропорционально одному показателю-сомножителю, а высота — второму показателю-сомножителю. Тогда произведение этих показателей, т.е. третий показатель, будет изображаться площадью прямоугольника (рис.)
Пример. Имеются данные за 2010 г. о валовом сборе картофеля, урожайности посевных площадей в одном из регионов (табл. 4.2).
Таблица 4.2. Данные о валовом сборе картофеля и урожайности
|
Вид продукта |
Посевная площадь, тыс. га |
Валовый сбор, тыс. т |
Урожайность, с 1 га убранной площади |
|
Картофель |
4,3 |
104,7 |
244,8 |
Примем 2 см = 1 тыс. га; 1 см = 50 ц/га. Проверка взаимосвязи:
Посевная площадь = Валовой сбор/Урожайность;
4,3=104 700/24 480.
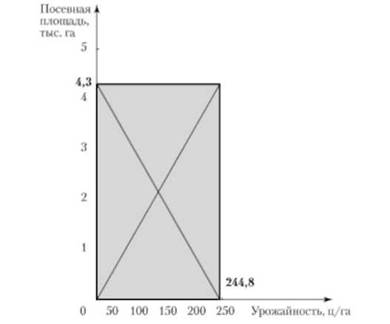
Рис. 4.10. Зависимость валового сбора картофеля от урожайности и посевной площади в одном из регионов в 2010 г.