Классификация моделей систем

В параграфе 1.1 была приведена первоначальная классификация моделей, в соответствии с которой модели делили на две группы — физические и абстрактные (математические).

Физическими моделями называют модели, эквивалентные или подобные оригиналу, но имеющие другую физическую природу, и делят их на натуральные, квазинату рольные, масштабные, аналоговые.

Математические модели представляют собой формализованное отображение системы с помощью абстрактного языка, с помощью математических соотношений, отражающих структуру или процесс функционирования системы, и делятся на аналитические и численные. Аналитические модели — на детерминированные и вероятностные.

В качестве детерминированных моделей, когда при исследовании случайные факты не учитываются, для представления систем, функционирующих в непрерывном времени, используются дифференциальные, интегральные и другие уравнения, а для представления систем, функционирующих в дискретном времени, — конечные автоматы и конечно-разностные схемы. Если проблемную ситуацию не удается отобразить детерминированными моделями, то применяются стохастические и другие типы моделей. Классификация моделей по виду методов моделирования и характеристика этих классов моделей приводится в гл. 3—5.

Однако с учетом рассмотренной в параграфе 1.3 классификации методов моделирования формализованное отображение системы с помощью абстрактного языка не сводится только к детерминированным и вероятностным моделям. К математическим можно отнести теоретико-множественные модели, модели математической логики, теории графов. А если в классификации принять название не "математические методы", а "методы формализованного представления систем", то к этому классу относятся и модели математической лингвистики (иногда кратко называемые лингвистическими), и семиотические модели.

К классу моделей формализованного представления систем относятся и модели, основанные на применении численных методов. А в составе численных методов выделяют особый класс математического программирования, который первоначально возникал и рассматривался как самостоятельный класс методов моделирования.

Численные методы математического программирования — раздел вычислительной математики, связанный с отысканием решений задач математического программирования в тех случаях, когда затруднено получение строго математического решения. Численные методы оптимизации, численный вычислительный эксперимент считаются важным разделом теории моделирования систем. Численные методы и методы математического программирования подробнее охарактеризованы в гл. 2.

К математическим моделям в настоящее время относят также программные комплексы — пакеты программ для расчета на компьютере (прикладные, привязанные к предметной области и конкретному объекту, явлению, процессу, и общие, реализующие универсальные математические соотношения, формально-логические модели, созданные на формальном языке).

В поисках термина для выделения класса моделей, объектов и процессов, которые не могут быть сразу отображены аналитическими и другими формализованными моделями, предлагалось классифицировать модели по степени абстрагирования, выделяя наряду с формальными и формализованными моделями словесные. Однако словесное, точнее вербальное (в терминах предметной области), отображение задачи моделирования обычно считают постановкой задачи, а не моделью, а в качестве этапа процесса моделирования рассматривают процесс перевода вербального описания в формальное или формализованное.

При моделировании систем применяется широкий спектр символических представлений, использующих "язык" классической математики. Однако далеко не всегда эти символические представления адекватно отражают реальные сложные процессы, и их в этих случаях, вообще говоря, нельзя считать строгими математическими моделями.

Большинство из направлений математики не содержит средств постановки задачи и доказательства адекватности модели. По образному выражению С. Лема, математика "изгнала беса (значение) из своих пределов и закрыла за ним врата на все засовы".

Адекватность моделей в прикладных направлениях, основанных на методах классической математики, доказывается экспериментом, который по мере усложнения проблем становится также все более сложным, дорогостоящим, не всегда бесспорен и реализуем.

В то же время моделирование, процесс формирования или выбора модели всегда связаны с содержательным анализом решаемой задачи, осуществляемым человеком, субъектом в определении (1.1). В простейших задачах арифметики, алгебры, геометрии содержательному анализу обучают на примерах. Однако по мере усложнения задач этап осмысления, постановки задачи становится все более сложным.

Поэтому возникали новые направления аналитических методов, которые имеют некоторые средства, помогающие осуществлять содержательный анализ задачи в процессе формирования математической модели (развитие аналитических методов моделирования систем рассматриваются в гл. 2), новые классы методов формализованного представления — статистические, теоретико-множественные, математическая логика и т.д. (рассматриваемые в гл. 3—5). Кроме того, помимо формальных и формализованных моделей, основанных па математических методах, в классификации методов моделирования систем, рассмотренной в параграфе 1.3, был выделен особый класс моделей, основанных на методах активизации интуиции и опыта специалистов (гл. 7). В числе моделей, основанных на МАИС, можно также выделить классы моделей выработки коллективных решений, сценариев (которые можно считать словесными, или вербальными моделями), моделей структуризации, морфологических моделей, моделей организации сложных экспертиз.

Самостоятельными разделами теории моделирования можно также считать специальные методы или подходы, приведенные в середине классификации методов на рис. 1.3, сочетающие средства МАИС и МФПС, — ситуационное, структурно-лингвистическое, когнитивное, логико-лингвистическое, лингво-комбинаторное моделирование, моделирование, основанное на информационном подходе к анализу систем, моделирование путем организации процесса постепенной формализации с переключением МАИС и МФПС, обеспечивающее переход от менее формализованной модели к более формализованной.

Можно отдельным классом считать и класс моделей, основанных на комплексированных методах, т.е. говорить о топологических, графо-семиотических и т.п. моделях.

С методами имитационного динамического, логико-лингвистического, лингво-комбинаторного, ситуационного, когнитивного моделирования лучше знакомиться в работах их авторов. В данном учебнике рассматриваются специальные методы, теории систем и системного анализа, развиваемые авторами (гл. 6).

Как было сказано, в числе математических в определенный период развития теории моделирования начали выделять класс имитационных моделей.

Имитационная модель в исходном понимании — описание системы и внешних воздействий, алгоритмов функционирования системы или правил изменения ее состояния под влиянием внешних и внутренних возмущений в ситуациях, когда алгоритмы и правила не дают возможности использования имеющихся математических методов аналитического и численного решения, но позволяют имитировать процесс функционирования системы и производить вычисления интересующих характеристик. В последующем имитационные модели стали создавать для гораздо более широкого класса объектов и процессов, чем аналитические и численные.

На базе статистических представлений разработаны: направление имитационного моделирования с целью определения функции распределения случайной величины; моделирование, основанное на методе Монте-Карло (см. параграф 3.3); имитационное моделирование в теории массового обслуживания (см. параграф 3.5).

Поскольку для реализации имитационных моделей служат вычислительные системы, в качестве средств формализованного описания имитационной модели используют универсальные и специальные языки. Для моделирования могут быть использованы языки имитационного моделирования (ЯИМ) и общего назначения (ЯОН).

Для исследования, разработки прогнозов и для решения других задач принятия решений разработаны специальные методы имитационного моделирования — имитационное динамическое моделирование Дж. Форрестера, имитационное моделирование с использованием автоматизированной системы PILGRIM, развиваемое А. А. Емельяновым.

В условиях активного развития компьютерного моделирования формируется самостоятельный класс моделей представления и извлечения знаний, в составе которых выделяют модели, развиваемые на базе теории искусственного интеллекта, модели, построенные на принципах, заимствованных у природы, модели интеллектуального анализа данных (ИАД) — Data Mining. Обобщенная классификация и краткая характеристика моделей представления и извлечения знаний приведена в гл. 8.

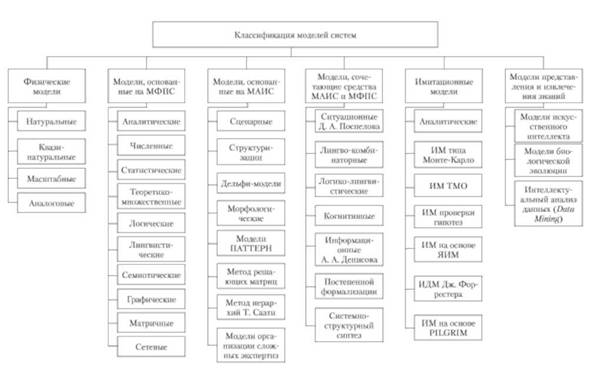
Рис. 1.4. Классификация моделей

На рис. 1.4 приведены укрупненные разделы классификации моделей по признаку "методы моделирования", детализировать которые позволит характеристика методов моделирования, рассматриваемая в последующих главах учебника.

В последующих главах кратко охарактеризованы выделенные группы методов, включая: основной понятийный, терминологический аппарат методов соответствующего класса; направления (теоретические и прикладные), которые возникли и развиваются на базе представлений соответствующего класса; преимущества и недостатки методов, области (сферы) их применения и ограничения с точки зрения моделирования сложных процессов и проблем.