Изотермические пламена. Определяющая роль диффузии активных центров

Развитие теории разветвленных цепных реакций и успешное применение ее к количественному описанию взрыва в газовых смесях, включая критические условия, период индукции, действие ингибиторов, кинетику реакции, – эти успехи цепной теории были поистине впечатляющими. Поэтому, естественно, возник вопрос: нельзя ли рассматривать распространение пламени как явление, обусловленное разветвлением цепей? Нельзя ли предположить, что в зоне реакции велика концентрация активных частиц и соответственно велика скорость разветвления и количество вновь образующихся активных частиц? Эти частицы могут диффундировать в "свежую", еще не реагирующую смесь и создать там начальную концентрацию, необходимую для дальнейшего разветвления цепей.

В 1937 г. появилась замечательная работа И. Г. Петровского, А. Н. Колмогорова, Н. С. Пискунова, которая дала математический аппарат и выражение для скорости распространения волны в очерченных выше предположениях.

Работа была задумана ее авторами применительно к биологической задаче: в экологической среде внезапно, локально (в некотором очаге) возникает новый тип организмов, обладающий повышенным биологическим потенциалом (лучшая приспособленность к условиям данной среды, большая плодовитость) по сравнению с ранее существовавшим, и этот новый тип расселяется по всему пространству, вытесняя старый тип организмов. Однако при использовании теории И. Г. Петровского, А. Н. Колмогорова, Н. С. Пискунова применительно к химическим реакциям и пламенам обнаруживается принципиальная трудность.

Действительно, в работе предполагается, что среда, окружающая очаг, является активной, сверхкритической, т.е. в любой точке среды активные частицы начинают размножаться немедленно после их возникновения. При этом вне очага активные частицы появляются только за счет диффузии. Иначе обстоит дело в химически активной среде: спонтанное появление активных частиц за счет теплового движения неизбежно, а значит, неизбежно и возникновение новых независимых очагов, что нарушает картину закономерного распространения химической реакции в виде фронта, с постоянной скоростью удаляющегося от первоначально заданного очага.

Можно сформулировать эту трудность иначе. Экспериментальные наблюдения показывают, что взрывчатые смеси в начальном своем состоянии (обычно при комнатной температуре) являются подкритическими по отношению к разветвлению цепей, т.е. константа скорости обрыва цепей g больше константы скорости разветвления, так что φ < 0. Таким образом, ситуация принципиально отличается от гой, которая рассматривалась в работе И. Г. Петровского, А. Н. Колмогорова, Н. С. Пискунова.

Обычно в пламенах происходит именно цепная реакция с разветвлением цепей. При этом процесс разветвления цепей, скорость которого сильно зависит от температуры, протекает активно лишь в смеси, нагретой до значительно более высокой температуры, чем начальная температура смеси. Этот нагрев осуществляется за счет теплопроводности. Поэтому несмотря на цепной характер реакции распространение пламени обусловлено и цепным, и тепловым механизмами, т.е. и диффузией активных центров, и теплопроводностью.

В Институте химической физики РАН особый интерес вызывала ситуация, когда распространение пламени не сопровождается сколько-нибудь заметным разогревом, волновой режим распространения химической реакции по горючей смеси осуществляется при практически постоянной температуре. Такие "холодные" пламена давно были известны для целого ряда горючих смесей, горящих при низких давлениях, в частности для смеси сероуглерода с кислородом, углеводородов и др. При изучении холодных пламен надо быть уверенным, что тепловое ускорение химической реакции, ответственное за распространение горячих пламен, не играет сколько-нибудь существенной роли. Поэтому, чтобы свести к минимуму возможный разогрев смеси, используют очень бедные горючие смеси, в которых адиабатический разогрев не превышает несколько градусов.

В таких условиях, несомненно, имеет место диффузионное распространение цепной реакции. Но как совместить этот факт с устойчивостью исходной смеси с тем, что в исходном своем состоянии при начальной температуре смесь не воспламеняется, так что φ < О?

Ответ на этот вопрос дает концепция взаимодействия цепей.

Как мы видели, в случае процессов обрыва и разветвления цепей, линейных по концентрации активных центров, области самовоспламенения отвечает неравенство f >g, т.е. положение границы полуострова воспламенения не зависит от скорости зарождения цепей и исходной концентрации активных центров.

Однако в принципе возможны реакции, скорость которых нелинейно зависит от концентрации активных центров; это реакции взаимодействия активных центров типа B1 + В2 = = В3 + В4 + В5, приводящие к размножению, разветвлению цепей. При взаимодействии цепей скорость реакции зарождения может приводить к изменению области самовоспламенения. Рассмотрим в качестве примера основное уравнение цепной теории (3.42) при положительном квадратичном разветвлении цепей ("квадратичный автокатализ"):

(3.165)

Цепное воспламенение происходит, если dn/dt > 0 – квадратный трехчлен в правой части (3.165) положителен. Это возможно не только при f > g, как в случае линейных процессов разветвления и гибели, но и при f < g' при этом, если W0 мало, в начальном состоянии смесь практически не реагирует и устойчива. Разветвление цепей возможно, если концентрация активных центров превзойдет определенное критическое значение . Исходная смесь в начальном состоянии устойчива и тем не менее способна поддерживать горение при диффузии, приводящей к п > n•. Таким образом, взаимодействие цепей, которое приводит к нелинейному увеличению числа активных центров и общей скорости химического превращения (поэтому его называют положительным), смещает границу полуострова воспламенения в область более низких температур. Возникает задача о цепном распространении холодного пламени при наличии квадратичного взаимодействия цепей – задача особенно интересная для развития цепной теории. Исходное состояние горючей смеси отвечает подкритическому состоянию вещества, в котором линейные процессы размножения и гибели активных центров не могут вызывать самовоспламенения – иначе горючая смесь сразу воспламенилась бы по всему объему. Возбудить цепную реакцию в исходной смеси можно, только если в системе существует механизм нелинейного взаимодействия цепей, приводящий к прогрессирующему росту концентрации активных центров. Однако для его ввода в действие необходима пороговая критическая концентрация активных центров, введенная в смесь в начальный момент. В холодном пламени критическая концентрация обеспечивается диффузией активных центров вперед по ходу распространения пламени из зоны интенсивной химической реакции, где активных центров много. Именно диффузия приводит к смещению границ полуострова воспламенения в исходной горючей смеси, обеспечивая разгон химического превращения.

Эти представления были полностью подтверждены в работе В. Г. Воронкова и Н. Н. Семёнова^[1] по исследованию холодного пламени окисления сероуглерода. Опыты показали, что пламя в бедной смеси 0,03% CS2 + воздух распространяется при температурах, которые в среднем на 100° ниже температур самовоспламенения смеси при соответствующих давлениях (рис. 3.29).

Рис. 3.29. Полуостров самовоспламенения (1) и граница области возникновения холодного пламени (2) в смеси сероуглерода с воздухом

Основным уравнением теории изотермического распространения пламени является уравнение диффузии промежуточного активного вещества в движущейся среде:

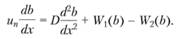(3.166)

Это уравнение написано в системе координат, связанной с пламенем, слева (x < 0) – свежая смесь, справа (х > 0) – продукты реакции, b – концентрация активного центра, D – его коэффициент диффузии, W1 – скорость размножения активных центров, W2 – скорость их гибели вследствие обрыва цепей. Естественно, следует полагать, что при отсутствии активных центров (b = 0) W1 = W2 = 0.

Скорости размножения активных центров и их гибели зависят, помимо концентрации самих активных центров, от концентрации других компонент реагирующей смеси, диффундирующих в холодном пламени. Поэтому теоретическое рассмотрение холодных пламен, как правило, требует анализа системы уравнений диффузии для различных компонентов смеси.

Здесь мы ограничимся самым простым случаем автокаталитической цепной реакции с квадратичным разветвлением цепи и при недостатке в смеси одного из исходных горючих компонентов. К этой схеме может быть сведена при использовании ряда упрощающих предположений кинетическая схема распространения пламени в смеси сероуглерода с кислородом.

Будем рассматривать два процесса: разветвление цепи –

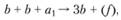(3.167)

где a1 – горючее вещество, находящееся в недостатке (фактически процесс квадратичного разветвления идет намного сложнее – через несколько элементарных актов, написанная реакция – суммарное представление разветвления); f – суммарная константа реакций, и объемную гибель активных центров –

(3.168)

где a2 – исходное вещество, находящееся в избытке (фактически g' может быть разностью между скоростями гибели активных центров и линейного разветвления).

Поскольку скорость разветвления цени намного больше скорости гибели центров, можно полагать, что

(3.169)

где а0 – начальная концентрация горючего вещества. Для такой разветвленной реакции

(3.170)

и уравнение (3.166) принимает вид

(3.171)

с граничными условиями

(3.172)

где конечное значение концентрации промежуточного вещества определяется из равновесия в продуктах сгорания W1(bf)= W2(bа).

Переходя к переменной я = b/bf и вводя функцию v == (D/(fbfa0))1/2dz/dx, понизим порядок уравнения (3.171):

(3.173)

Поскольку концентрации на стремятся к постоянным значениям, граничными условиями уравнения (3.173) являются

(3.174)

Будем искать решение уравнения (4.173) в виде

(3.175)

(граничные условия при этом удовлетворяются на обоих концах отрезка).

Подставляя предполагаемое решение (3.175) в уравнение (3.173), можно убедиться, что оно удовлетворяется, если выполняется соотношение

(3.176)

Таким образом, для скорости распространения холодного пламени получаем формулу

(3.177)

или приближенно, при малом значении параметра ,

(3.178)

Эта формула была применена В. Г. Воронковым и Η. Н. Семёновым к обработке экспериментальных данных по распространению холодного пламени в бедной смеси сероуглерода с воздухом (0,03% CS2) (адиабатический разогрев в такой смеси составляет 15°, условие изотермичности процесса хорошо выполняется).

Из формулы (3.177) видно, что скорость пламени существенно зависит от отношения констант гибели активных центров и разветвления цепи. Если это отношение (g/f) растет, то скорость пламени уменьшается, и по достижении становится равной нулю. Таким образом, в самой формуле (3.177) заложены пределы распространения холодного пламени; гибель активных центров, естественно, способствует прекращению горения, разветвление цепи – интенсивному распространению пламени. Отметим, что скорость распространения на пределе горения обращается в нуль, в то время как в опытах по горению сероуглерода наблюдались ненулевые минимальные значения скорости. Это несоответствие объясняется приближенным характером теории, рассматривающей изменение концентрации только одного химического компонента вместо сложного процесса химического превращения с участием многих реагентов.

Метод получения формулы для скорости распространения пламени, использованный в этом разделе, хотя и дает точное значение скорости (это точное решение уравнения), но оставляет открытым вопрос о единственности решения. Возникает вопрос: нельзя ли построить несколько режимов распространения холодного пламени, удовлетворяющих всем условиям?

Как уже говорилось выше, математическому исследованию вопроса о возможных волновых режимах распространения изотермической цепной химической реакции посвящена работа И. Г. Петровского, А. Н. Колмогорова, Н. С. Пискунова, в которой доказывается, что, вообще говоря, можно построить бесконечное число решений задачи, однако устойчивым из них является только одно, отвечающее минимально возможному значению скорости. Этот факт имеет место, если суммарная скорость реакции W1(b) – W2(b) положительна при b > 0, обращается в нуль при b = 0 и имеет в этой точке максимальную положительную производную по b. Но в рассмотренном выше случае производная скорости реакции при b = 0 отрицательна, и решение задачи оказывается единственным, т.е. вопрос о скорости изотермического пламени при автокатализе второго порядка решается однозначно.

Отметим особенности теории распространения холодного пламени, отличающие ее от теории теплового распространения. При тепловом распространении пламени химическая реакция сосредоточена в узкой зоне вблизи температуры горения, и в пламени можно выделить зону прогрева (без химической реакции), зону химической реакции и в каждой зоне находить упрощенные решения основного уравнения. При диффузионном механизме распространения изотермического пламени выделить различные по своему физическому значению зоны внутри фронта пламени нельзя: цепная химическая реакция идет по всей толщине фронта.

Само распространение холодного пламени можно трактовать как непрерывное внесение затравки – через диффузию – в свежую смесь. Поэтому скорость пламени задается локальной формой функции скорости производства активных центров вблизи границы холодного пламени со свежей смесью (при b → 0) и не зависит от вида этой функции внутри фронта холодного пламени. При тепловом распространении пламени скорость, напротив, определяется интегралом от скорости тепловыделения по всей зоне химической реакции.

Подчеркнем, что чисто тепловой и чисто диффузионный механизмы распространения ламинарного пламени являются идеализированными предельными случаями реальных ситуаций. В действительности, передача тепла всегда сопровождается диффузией активных частиц (а большинство реакций в пламенах, по-видимому, цепные!), равно как верно и обратное утверждение, потому что цепные реакции обладают, как правило, большим тепловым эффектом. Кроме того, скорости элементарных стадий цепного превращения обладают существенными энергиями активации и, следовательно, сильной зависимостью от температуры. Изотермичность цепных реакций достигается лишь в случае сильного разбавления горючей смеси инертными газами.

Поэтому представляет большой интерес исследование горячих пламен с цепными реакциями.

До сих пор, рассматривая ламинарное пламя, мы предполагали, что существует распространяющийся с постоянной скоростью плоский фронт пламени с устойчивой тепловой и диффузионной структурой. Этот факт не ставился под сомнение. Однако часто в опытах наблюдается распад плоского фронта пламени на отдельные очажки горения – образуются так называемые ячеистые пламена; например, факел пламени на горелке Бунзена трансформируется в пирамидальное пламя, иногда даже вращающееся вокруг своей оси, при распространении пламени в трубах часто возникает колеблющийся фронт горения и т.п. Эффекты эти часто связаны с внутренней неустойчивостью плоского ламинарного пламени, которая не позволяет ему сохраняться продолжительное время. Установлено несколько причин, по которым пламя оказывается неустойчивым. К неустойчивости пламени могут приводить процессы теплопроводности и диффузии, ответственные за структуру его фронта, и газодинамические возмущения в горючей смеси и продуктах сгорания. Роль теплодиффузионных процессов проявляется в их влиянии на мелкие возмущения, которые воздейст вуют на саму структуру фронта пламени, но не вызывают значительных газодинамических возмущений. Газодинамические возмущения, напротив, имеют большой масштаб, намного превышающий теплодиффузионную ширину.

В 1934 г. Б. Льюис и Г. Эльбе [25], рассматривая изменение полной энтальпии внутри пламени (см. рис. 3.26), пришли к заключению о том, что при коэффициенте температуропроводности х, большем коэффициента диффузии D, пламя должно быть неустойчивым. Свой вывод они объяснили тем, что при подобном соотношении между коэффициентами переноса в зоне подогрева существует максимум полной энтальпии – пламя "вобрало" в себя избыточную энергию, т.е. пришло в состояние, в котором, как правило, система оказывается неустойчивой.

Дальнейшие теоретические и экспериментальные исследования показали, однако, что вывод Льюиса и Эльбе не является исчерпывающим. При x> D пламя может быть при определенных условиях неустойчивым. Но имеется и неустойчивость другого типа, возникающая при противоположном соотношении между коэффициентами переноса. Почему она появляется, лучше всего пояснить на рисунке (рис. 3.30).

Рис. 3.30. К иллюстрации диффузионно-тепловой неустойчивости пламени при D > х по отношению к искривлениям его фронта. Область продуктов горения заштрихована, сплошными стрелками показано направление тепловых потоков, пунктирными – диффузионных потоков

Рассмотрим искривленный фронт ламинарного пламени. Если исследовать влияние на искривление пламени одной теплопроводности, то можно убедиться, что теплопроводность должна уменьшать искривление пламени – приводить к его стабилизации. Действительно, выпуклые по отношению к холодной горючей смеси участки зоны химической реакции должны отдавать больше тепла, чем в плоском пламени: тепло от них передается не только вперед по направлению распространения пламени, но и в боковых направлениях. Вызываемое этим охлаждение зоны реакции приведет к отставанию вырвавшихся вперед участков пламени. Иная ситуация будет для вогнутых участков, где по тем же соображениям температура повысится, скорость реакции увеличится, и они с большей скоростью будут распространяться вперед но ходу распространения пламени. Таким образом, поверхность искривленного фронта пламени будет выравниваться. Иначе говоря, теплопроводность оказывает стабилизирующее действие на искривленное пламя.

К противоположному выводу можно прийти, если рассматривать диффузию лимитирующего реакцию горючего компонента. Выпуклые участки фронта находятся в более благоприятном для поставки горючего материала положении, чем другие участки фронта пламени, – они диффузией собирают горючее вещество с большего объема горючей смеси (см. пунктирные стрелки на рис. 3.30). Благодаря диффузии скорость реакции на выпуклых участках увеличится, и искривления фронта тем самым еще больше возрастут. Диффузия, таким образом, оказывает дестабилизирующее действие. Окончательный ответ о диффузионно-тепловой устойчивости пламени зависит от соотношения между процессами диффузии и теплопроводности. При х> D естественно ожидать существование плоского фронта пламени, а при обратном соотношении уходящие вперед выпуклые языки пламени настолько обедняют смесь, остающуюся в промежутках между ними, что она становится негорючей, фронт пламени разбивается на отдельные несвязанные между собой выпуклые участки. Неустойчивость пламени при х < D по отношению к искривлениям его фронта была установлена Я. Б. Зельдовичем [15]; количественный расчет этого явления сделан Г. М. Махвиладзе и В. И. Мышенковым^[2].

Распад плоского фронта пламени па отдельные очаги горения наиболее наглядно прослеживается в экспериментах с горючими смесями, компоненты которых – горючее и окислитель – имеют резко отличающиеся молекулярные веса и, следовательно, резко различные коэффициенты молекулярного переноса. Примером такой горючей смеси является смесь водорода с бромом. Если в ней в недостатке находится легкий газ – водород, то реализуется условие, когда коэффициент диффузии лимитирующего скорость химической реакции компонента оказывается больше коэффициента температуропроводности смеси, который определяется теплопроводностью преобладающего, тяжелого компонента. В этом случае – в бедной водородом смеси – плоское пламя оказывается неустойчивым. В экспериментах, которые впервые проводил с бромо-водородными смесями В. И. Кокочашвили, наблюдается образование отдельных колпачков или очажков пламени с характерным размером ~1 см, которые движутся в горючей смеси гак, что поверхность фронта горения не захватывает при этом всего сечения трубы. За колпачками тянутся суживающиеся светящиеся следы горючего газа длиной до 30-40 мм. Размер очажков, их форма, устойчивость зависят от вида пламени: например, для быстро горящих пламен очажки (ячейки) меньше, но они более устойчивы.

В случае если в бромо-водородной смеси в недостатке тяжелый бром, наблюдается устойчивый плоский фронт пламени. Соотношение между диффузией и теплопроводностью при этом таково, что возмущения на фронте пламени сглаживаются.

Четкие опыты по определению влияния состава смеси на распад пламени были проведены В. П. Карповым, который изучал распространение сферического пламени в бомбе постоянного объема для разных горючих смесей и разных составов с помощью шлирен-киносъемки. Было показано, что для смесей водорода с воздухом при недостатке водорода поверхность пламени начинает быстро дробиться на отдельные ячейки, тот же эффект наблюдается для бутано-воздушных смесей, но уже с недостатком воздуха. В смесях же "метан – воздух" ячейки не образовывались. Иначе говоря, неустойчивость пламени была обнаружена в тех случаях, когда в недостатке оставалась компонента меньшего молекулярного веса (наиболее легко диффундирующая).

В связи с диффузионно-тепловой неустойчивостью ламинарного фронта пламени следует обратить внимание читателя на еще один в принципе возможный механизм горения горючего газа. Можно представить себе сферический объем, заполненный продуктами сгорания, имеющий высокую температуру и покоящийся относительно газа; к поверхности объема диффузией подаются реагирующие компоненты, а продукты реакции также диффузией отводятся в объем окружающего холодного газа. Химическая реакция протекает в узком сферическом слое на поверхности "шарика" пламени, выделяющееся в реакции тепло теплопроводностью передается в холодные области горючей смеси. Из-за разности в коэффициентах диффузии и температуропроводности температура внутри "шарика" может отличаться от термодинамической температуры горения.

Так, при горении горючих смесей с участием водорода соотношение между диффузией и теплопроводностью, как уже говорилось, резко сдвигается. Из-за большого коэффициента диффузии легкого водорода "шарик" пламени собирает горючее – водород – с большого объема, а тепло отдает малому объему. Поэтому достигается подъем температуры, намного превышающий теоретический по термодинамическому расчету, при котором полагается, что теплота реакции горючего, содержавшегося в определенном объеме, идет на нагревание всей массы продуктов горения, образовавшихся из смеси, находившейся в этом объеме.

Можно построить теоретическую модель стационарного сферического диффузионного горения. Оказывается, однако, что полученное решение является абсолютно неустойчивым в диффузионно-тепловом смысле. Это не означает еще, что сферическое диффузионное горение перемешанной горючей смеси нельзя рассматривать как возможный режим горения, к которому переходит система после распада плоского ламинарного пламени. Стабилизирующую роль могут играть потери на излучение, которые не учитывались в [14]. Кроме того, как показывают эксперименты, очаги горения движутся относительно горючей смеси, и стабилизация достигается, по-видимому, за счет совместного действия газодинамических и диффузионно-тепловых факторов.

Обогащение горючей смеси в зоне реакции быстрее диффундирующей компонентой исследовалось экспериментально в водородо-кислородной смеси К. Клузиусом. В этой работе часть обычного водорода заменялась на более тяжелый дейтерий. Химический анализ газа при ячеистом горении показал, что горючая смесь вдали от пламени обогащается медленно диффундирующим дейтерием.

В заключение обсуждения диффузионно-тепловых аспектов устойчивости ламинарного горения отметим, что гипотеза Льюиса – Эльбе о неустойчивости фронта пламени при избытке полной энтальпии правильно предсказывает возможность одномерной неустойчивости горения. Она приводит, в частности, к правильному результату (при соблюдении еще некоторых дополнительных условий) в случае, когда коэффициент диффузии горючего компонента в некоторой части зоны подогрева очень мал или обращается в нуль (т.е. D << x)• Речь идет о стационарном послойном горении конденсированных взрывчатых веществ и порохов [16]. При их горении структура зоны прогрева усложняется: в нее входит зона прогрева конденсированного вещества (и там D = 0) до температуры его разложения в газ и зона прогрева образующихся продуктов газификации. Зона прогрева в конденсированном веществе в этом случае играет роль аккумулятора тепла, в ней как раз и достигается максимум полной энтальпии. Взаимодействие этого аккумулятора тепла с зоной химической реакции в газе над поверхностью топлива (они связаны тепловыми потоками и потоками вещества) при определенных условиях приводит к прогрессирующему росту малых возмущений, т.е. к неустойчивости.

Другой причиной, вызывающей неустойчивость плоского фронта ламинарного пламени, являются дозвуковые газодинамические возмущения в горючей смеси в продуктах сгорания. В 1944 г. Л. Д. Ландау выполнил ставшее классическим исследование но теории горения^[3]. Он проанализировал устойчивость плоского фронта ламинарного пламени, рассматриваемого как газодинамический разрыв, к пространственным искривлениям, вызванным возмущениями движения холодной горючей смеси и продуктов сгорания. Анализ привел к парадоксальному выводу: ламинарное пламя всегда неустойчиво (гидродинамическая неустойчивость пламени). В то же время на практике часто наблюдается настоящее ламинарное пламя – на горелках, в камерах сгорания и т.п., области существования ламинарных пламен достаточно широки.

Противоречие между теорией и экспериментом объясняется тем, что в реальных условиях горения существует много факторов, стабилизирующих гидродинамическую неустойчивость ламинарного фронта пламени; это – диффузия и теплопроводность, вязкость горючего газа и продуктов сгорания, неоднородное поле скоростей перед фронтом пламени, кривизна фронта пламени и др.

Еще одной причиной, влияющей на устойчивость плоского пламени, является действие силы тяжести. Влияние ускорения на поверхность газодинамического разрыва в зависимости от направления ускорения может дополнительно стабилизировать или дестабилизировать пламя. Поэтому при проведении экспериментов с пламенем в вертикальных трубах распад сплошного фронта пламени на отдельные очажки при его распространении вверх происходит скорее, чем при распространении вниз; отличаются также и концентрационные пределы распространения пламени.

Влияние тейлоровской неустойчивости (неустойчивость в поле тяжести горизонтальной границы раздела между двумя жидкостями разной плотности, причем более тяжелая жидкость находится сверху) при распространении пламени тем сильнее, чем меньше скорость пламени, и поэтому этот эффект особенно ярко проявляется вблизи пределов распространения пламени.