В чем заключается метод скользящего среднего?

В методе скользящего среднего можно выделить разновидности: метод простого подвижного (скользящего) среднего и метод взвешенного скользящего среднего.

Рассмотрим метод простого подвижного (скользящего) среднего. Он заключается в том, что прогнозируемый показатель рассчитывается как усредненное значение этого показателя за несколько предыдущих моментов времени. В общем случае формула выглядит так:

(5.1)

где fk – прогноз продаж на момент времени tk. N – число предшествующих моментов времени, используемых при расчете; хk-i – реальное значение показателя в момент времени tk-i.

Пример 5.1

Спрогнозируем объемы продаж продукции компании ХКО методом простого подвижного (скользящего) среднего на август 2013 г. Исходные данные для расчетов приведены в табл. 5.1.

Таблица 5.1

Объем продаж компании ХКО с октября 2012 г. по июль 2013 г. (тыс. штук)

t	1	2	3	4	5	6	7	8	9	10	11
x	7	6	8	9	8	10	11	11,5	10	12	–

В рассматриваемом примере примем значение N =3. Результаты расчетов по формуле 5.1 приведены в табл. 5.2.

Таблица 5.2

Прогноз объема продаж компании ХКО на август 2013 г., метод простого скользящего среднего

t	1	2	3	4	5	6	7	8	9	10	11
x	7	6	8	9	8	10	11	11,5	10	12	–
f	–	–	–	7,2	8,1	8,3	9,2	9,8	11,1	10,65	11,3

Здесь

и т.д.

Метод взвешенного скользящего среднего является естественным расширением метода простого скользящего среднего. В нем учитывается то, что данные за прошедшие периоды времени влияют на возможные изменения неодинаково. Для этого вводится понятие "вес". Удобно в качестве весов брать доли, демонстрирующие степень влияния данных исходного временно́го ряда в зависимости от их удаленности от прогнозируемых. В этом случае их сумма, очевидно, будет равна единице. Формула для расчетов будет выглядеть так:

(5.2)

где wk-i – вес, с которым показатель xk-i используется в расчетах. Пример 5.2

Используя исходные данные примера 5.1 и предполагая, что N = 3, w1 = 2, w2 = 3, a w3 = 5, получим следующие результаты (табл. 5.3).

Таблица 5.3

Прогноз объема продаж компании ХКО на август 2013 г., метод взвешенного скользящего среднего

t	1	2	3	4	5	6	7	8	9	10	11
x	7	6	8	9	8	10	11	11,5	10	12	–
f	–	–	–	7,2	8,1	8,3	9,2	9,8	11,1	10,65	11,3

Здесь и т.д.

Как использовать метод экспоненциального сглаживания?

При расчетах по методу экспоненциального сглаживания используется формула

(5.3)

где l – постоянная сглаживания, число из интервала (0; 1), определяющее степень сглаживания.

Важно отметить, что в методе экспоненциального сглаживания важную роль играет субъективный выбор двух параметров: прогноза на первый используемый момент времени f1 и постоянной сглаживания l. И если выбор начальных данных прогноза полностью зависит от опыта аналитика и имеющихся у него на момент начала расчетов данных, то постоянная сглаживания может быть выбрана методом проб и ошибок, основанном на последовательном приближении прогноза к реальным значениям. При использовании метода экспоненциального сглаживания для составления прогноза на предприятиях обычно используется своя постоянная сглаживания, проверенная временем.

Пример 5.3

Предположим, что в рассматриваемом примере f1, = 8; l = 0,4, полученные результаты приведены в табл. 5.4.

Таблица 5.4

Прогноз объема продаж компании ХКО на август 2013 г., метод экспоненциального сглаживания

t	1	2	3	4	5	6	7	8	9	10	11
x	7	6	8	9	8	10	11	11,5	10	12	–
f	–	7,6	6,96	7,376	8,03	8,02	8,812	9,69	10,414	10,25	10,95

Здесь

и т.д.

Результатом использования этого более тонкого метола является уточнение объема продаж.

Рассматриваемые нами в этом параграфе методы количественного прогнозирования подкупают своей простотой. Но внимательный читатель наверняка уже отметил некоторую ограниченность результата по времени, возможность прогнозирования лишь следующего шага. Это, безусловно, сужает круг проблем, для анализа которых могут быть использованы данные методы, но не умаляет их достоинств. Во многих более сложных моделях предложенные подходы используются для локальных расчетов, в этом мы сможем убедиться уже во втором параграфе данной главы. Кроме того, при анализе деятельности небольших предприятий верно выбранный метод прогнозирования и грамотно проведенное исследование способны предупредить о возможных негативных изменениях без особых затрат. Именно поэтому очень важно проводить расчеты с уже имеющимися данными. Это позволяет выбрать параметры, используемые в каждом из описанных выше методов (числа предшествующих периодов N и значения весов w в методе скользящего среднего, прогноза на начальный момент времени и подходящее значение постоянной сглаживания в методе экспоненциального сглаживания), соответствующие работе в спокойном режиме. И тогда отклонение прогнозного значения от "привычного" может стать первым замеченным сигналом о надвигающемся кризисе.

Остается открытым вопрос об оценке адекватности метода прогнозирования. Здесь возможны разные подходы, выбор которых весьма субъективен. Иногда достаточно совместить графическое представление реальных данных и результатов прогнозирования и выбрать визуально. Посмотрим, как это выглядит на основе рассмотренных выше методов простой и взвешенной скользящих средних (рис. 5.1, 5.2).

Рис. 5.1. Метод простого скользящего среднего

Рис. 5.2. Метод взвешенного скользящего среднего

Визуальный анализ графиков дает нам основание предположить, что в нагнем случае метод подвижного среднего дает не самый точный результат. Можно попытаться исправить ситуацию с помощью вариации весов в методе взвешенного скользящего среднего, но лучше проверить качество прогнозов другими методами.

Полезно рассчитать для них коэффициент корреляции, например, ранговой корреляции Спирмена. Напомним, что формула для его вычисления выглядит так:

(5.4)

где di – разница рангов соответствующих величин.

Для демонстрации процесса расчета ранговой корреляции воспользуемся данными, полученными при расчете методом экспоненциального сглаживания. Ниже приведена табл. 5.5, содержащая исходные значения и их ранги.

Таблица 5.5

Таблица для вычисления коэффициента ранговой корреляции

Ранг х	9	7,5	6	7,5	4,5	3	2	4,5	1
X	6	8	9	8	10	11	11,5	10	12
F	7,6	7	7,4	8,03	8,02	8,8	9,7	10,4	10,2
Ранг f	7	9	8	5	6	4	3	1	2

Здесь

Ранжирование величин проводится по убыванию их значений. В случае, если значения повторяются (как в нашем примерев исходных данных), они нумеруются подряд, а затем получают ранги, равные среднему арифметическому рангов одинаковых величин. В нашем примере коэффициент корреляции Спирмена равен 0,75. Это показывает хорошее приближение динамики методом экспоненциального сглаживания с выбранными параметрами.

Когда полезен метод проецирования тренда?

В основе метода проецирования тренда лежит метод наименьших квадратов. С его помощью строится прямая (линейный тренд), состоящая из точек, которые в среднем наименее отклоняются от заданного ряда, и демонстрирующая направление изменения зависимости показателя х от V.

(5.5)

Здесь а и b – постоянные, подлежащие определению. Использование метода наименьших квадратов, широко применяющегося в математической статистике для формализации задач, позволяет записать систему уравнений для их вычисления:

(5.6)

Пример 5.4

Продолжим рассмотрение ситуации, представленной в примере 5.1, построим таблицу с необходимыми расчетными данными для построения линейного тренда (табл. 5.6).

Таблица 5.6

Построение линейного тренда

Расчетные данные											Σ
ti	1	2	3	4	5	6	7	8	9	10	55
xi	7	6	8	9	8	10	11	11,5	10	12	92,5
tixi	7	12	24	36	40	60	77	92	90	120	558
	1	4	9	16	25	36	49	64	81	100	385

Запишем систему уравнений

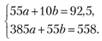
Отсюда: а = 0,6; b = 6.

Тем самым получим уравнение линейного тренда с помощью которого можно рассчитать как прогноз на следующий месяц:

так и значение для более удаленных моментов времени.

Нетрудно заметить, что метод проецирования тренда является прямым аналогом построения прямой регрессии, поэтому для проверки его надежности удобно использовать коэффициент линейной корреляции, рассчитываемый по формуле

(5.7)

В нашем примере r=0,91, и это показывает очень хорошее приближение. (Напомним, что коэффициент корреляции принадлежит отрезку [-1; 1], и чем ближе его значение к единице, тем ближе прямая зависимость между величинами, а чем ближе к минус единице – тем ближе обратная зависимость. При значениях коэффициента, близких к нулю, можно утверждать, что связь отсутствует.)

Таким образом, методы прогнозирования с использованием временных рядов дают нам простой и достаточно падежный инструментарий выявления отклонений и принятия на этой основе антикризисных мер.