Индексы цен в социально-экономическом анализе

Индексам цен принадлежит ведущая роль при изучении изменений цен во времени и пространстве. Известно, что попытки простейшего измерения динамики цен на различные товары имели место еще в XVI в. с наступлением эпохи капиталистических отношений и развитием внешнеторговой деятельности. В зарубежной экономической литературе считается, что наиболее ранними обобщающими показателями изменения цен были индексы, предложенные в 1735 г. французским экономистом Ш. Дюто и итальянским экономистом Д. Р. Карли в 1751 г.

Оба показателя имели существенный недостаток, ограничивающий их применение – игнорирование удельных весов товаров в общем товарообороте. Во второй половине XIX в. в практику расчетов индексов цен была введена агрегатная форма, в которой изменение цен увязывалось с конкретной массой товаров. Формула первого взвешенного агрегатного индекса цен, известная как индекс Ласпейреса, была предложена в 1871 г.:

где – количество товара в базисном периоде; и – цена единицы товара соответственно в отчетном и базисном периодах.

Таким аналитическим индексом пользуется Бюро статистики труда США для построения индекса оптовых цен. Базисной ценой

() в этом случае является скользящая средняя за три последних года, предшествующих анализируемому. Взвешивание осуществляется по физическому объему продукции базисного периода ().

Другой вид взвешенного агрегатного индекса – индекс Пааше:

где – количество товара в отчетном периоде.

Индекс цен Пааше представляет собой сравнение агрегированных цен, взвешенных по физическим объемам продукции текущего периода, а индекс цеп Ласпейреса – сравнение агрегированных цен, взвешенных по физическим объемам базисного периода. Индексы цен Ласпейреса и Пааше в связи с различиями в структуре весов дают неодинаковые результаты, разница в которых может достигать в случае долгосрочных и международных сопоставлений нескольких процентов. Это связано с тем, что обе формулы не отвечают тесту обратимости факторов и частично требованиям теста обратимости во времени.

Американским ученым И. Фишером, разработавшим тесты правильности построения индексов в работе "Построение индексов" (1927), была предложена формула средней геометрической из индексов Пааше и Ласпейреса. Она получила название "идеального" индекса цен, или индекса Фишера:

В этой формуле удовлетворяется одно из требований теории индексов – независимость от выбора базы сравнения. Этот индекс использовался незначительное время в расчетах Конъюнктурного института народного комиссариата финансов и ЦСУ СССР для расчета индексов покупных и продажных цен разного уровня в государственной, кооперативной и частной торговле. В настоящее время индекс Фишера используется главным образом в международных сопоставлениях ВВП. Следует отметить, что названные выше агрегатные индексы цен Пааше и Ласпейреса были построены значительно раньше английским экономистом Т. Манном (1609) и русским экономистом Ф. Вирсге (1803)^[1].

В мировой статистической практике и научных исследованиях применяются, хотя и значительно реже, и другие агрегатные индексы цен:

• индекс Лoy ,

где 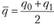– средняя величина реализации товаров за два или большее число периодов;

• индекс Джевонса ,

где и – цены базисного и отчетного года различных товаров; п – число товаров;

• индекс Маршалла, предназначенный для пространственнотерриториальных сопоставлений

или

Однако эти индексы цен широкого применения в отечественной статистической практике не нашли но разным причинам: из-за условности весов, отсутствия экономического содержания, трудностей в получении оперативной информации и др. Индексы цен в российской статистике рассчитываются на основе формул Ласпейреса и Пааше, что объясняется их четким экономическим смыслом, удобностью и оперативностью практических расчетов. Причем из-за последнего обстоятельства предпочтение отдается индексу Ласпейреса. В системе индексов цен, наряду с агрегатными формами индексов, широкое применение получили индивидуальные индексы цен и индексы средних цен. Индивидуальный индекс цен характеризует динамику цены конкретного товара (услуги):

где – цена на товар в текущем периоде; – цена на товар в предыдущем периоде; – цена товара в периоде, принятом за базу сравнения.

Согласно свойству круговой сходимости величина базисного индекса цен определяется как произведение цепных индексов. Например,

Индивидуальные индексы цен применяются при изучении динамики цен разнородной совокупности товаров и услуг. Они используются в различных модификациях агрегатных формул сводных индексов цен. Так, например, индексы Ласпейреса и Пааше можно записать в виде соответствующих формул среднеарифметической и среднегармонической:

В этих формулах индивидуальные индексы цен позволяют выявить роль отдельных товаров в формировании сводного индекса цен. При исчислении цепных и базисных общих индексов цен в статистической практике часто используется модифицированная формула Ласпейреса с рекурсивной системой расчета стоимостных весов. Она имеет следующий вид:

где – текущий период; – предшествующий период; 0 – базисный период.

В этой формуле изменение цен исчисляется на основе последовательных наблюдений цены, т.е. в каждый период времени базовые веса умножаются на последнее значение индекса цен.

Тем самым обеспечивается постоянная натуральная основа весов при изменении ее стоимостной оценки в соответствии с изменением цен по группам товаров. Кроме того, модифицированная формула является более универсальной по сравнению со стандартной формулой Ласпейреса, поскольку в ней используется непрерывная цепь вычислений, что облегчает задачу замены товаров при нестабильном состоянии производства и реализации. Пример расчета индекса цен приведен в табл. 25.6. Рассчитаем сводные индексы цен.

Цепные индексы цен:

а) январь к декабрю предыдущего года

б) февраль к январю

в) март к февралю

таким образом, в указанные периоды наблюдался незначительный рост цен на продукцию завода.

Базисные индексы цен:

а) январь к декабрю предыдущего года

Таблица 25.6

Методика расчета индекса цен на основе модифицированной формулы Ласпейреса

Виды продукции	Стоимость продукции, тыс. руб.				Стоимость продукции, тыс. руб.
		январь к декабрю	февраль к январю	март к февралю	январь в ценах декабря	февраль в ценах января	март в ценах февраля
А	1	2	3	4	5 = (гр. 2×гр. 1)	6 = (гр. 3×гр. 5)	7 = (гр. 4×гр. 6)
А	123	101,2	100,9	101,8	124,476	125,596	127,857
В	95	102,1	100,5	101,2	96,995	97,480	98,650
С	112	101,8	100,7	100,8	114,016	114,814	115,732
Итого	330	101,7	100,7	101,3	335.487	337,89	342,239

б) февраль к декабрю или

в) март к декабрю

или

или

т.е. за три месяца цены в марте но сравнению с декабрем выросли на 3,7%. Таким образом, рекурсивная система расчета индексов цен сводится к использованию в качестве весов для индексов цен текущего месяца к предыдущему весов базисного периода в ценах предшествующего месяца. По такой же методике рассчитываются индексы цен каждого периода (месяца, квартала) текущего года по сравнению с соответствующим периодом предыдущего года. Это позволяет частично устранить влияние сезонных колебаний на динамику цен. Одной из задач статистики является расчет средних цен по группам товаров (услуг) и анализ их изменения. Средние цены определяются как среднеарифметические взвешенные величины из уровней цен отдельных производителей или регионов. Средние цены по группам товаров (услуг) формируются под влиянием многих ассортиментных и территориальных структурных сдвигов, сезонных колебаний предложения и спроса и др. В связи с этим изменение средних цен на товары отличается по своему экономическому содержанию от индексов цен, исчисленных по отдельным товарам-представителям, прежде всего тем, что учитывает не только изменение конкретных цен на отдельные товары, но и влияние фактора структурных сдвигов.

Важнейшими факторами, определяющими структурные сдвиги, являются следующие: появление новых товаров, исчезновение старых, изменение доли отдельных товаров с различным уровнем цен, территориальные сдвиги в размещении производства и реализации товаров с региональной дифференциацией цен, сезонные колебания цен на сельскохозяйственную продукцию и т.д. В связи с этим средние цены не всегда могут быть использованы для характеристики динамики цен на основе метода временны́х рядов.

Индексный анализ динамики средних цен заключается в построении индексов переменного состава, постоянного состава и структурных сдвигов:

Между указанными индексами существует Вперед взаимосвязь:

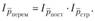
Если индекс постоянного состава рассчитывается по методике Ласпейреса (), то индекс структурных сдвигов соответ-

ственно имеет вид: . Следует помнить, что индексы постоянного состава и структурных сдвигов в различных схемах отличаются не только формулами, но и получаемыми результатами (за исключением случая, когда индекс постоянного состава равен единице). Индексы средних цен целесообразно рассчитывать при изучении цен как одного товара, так и однородных товарных групп по различным территориям и субрынкам. В этом случае структурный индекс отразит влияние изменения качества товара, перераспределения товарной массы, изменение структуры продаж и денежных доходов населения. Для примера возьмем данные о реализации картофеля за август и сентябрь на четырех рынках Санкт-Петербурга (табл. 25.7). Рассчитаем средние цены продажи картофеля по месяцам:

т.е. средние цены продажи картофеля снизились на 1,1%, хотя по каждому рынку в отдельности они не изменились. В индексе средних цен отразилось влияние изменения в структуре продаж картофеля и соответственно в структуре денежных расходов населения, которое совершает больше покупок на сравнительно дешевом рынке картофеля (доля продаж Южного рынка выросла с 20,4 до 26,6%):

Если использовать методику Ласпейреса, то получим такие же результаты.

Таблица 25.7

Данные реализации картофеля на рынках г. Санкт-Петербурга

Рынки	Август		Сентябрь		Структура продаж, %
	Объем продаж (<7о), тыс. кг	Цена 1 кг (р0), руб•	Объем продаж (¢0, тыс. кг	Цена 1 кг (pi), руб.
Кузнечный	450	15	480	15	39,8	36,5
Василеостровский	180	13	195	13	15,9	14,8
Торжковский	270	14	290	14	23.9	22,1
Южный	230	12	350	12	20,4	26,6
Итого	1130		1315		100,0	100,0