Взаимодействие и перенормировка
В квантовой теории поля концепты классической физики либо кардинально переосмысливаются, либо исключаются. Следует обратить в этой связи особое внимание на концепт взаимодействия. В классической физике взаимодействие передается полем от одной точки к другой. Так как в квантовой теории поля само представление о пространственной точке становится проблематичным, то классический концепт взаимодействия отвергается. Взаимодействие мыслится как рождение и поглощение частиц, соотносящееся с определенной пространственно-временной областью. Концепция близкодействия остается в силе, но протяженности и длительности интерпретируются в квантово-полевом ключе. Понятие скорости также становится квантово-полевым.
Механизм квантово-полевого взаимодействия получает наиболее четкое выражение в формулировке теории посредством использования лагранжианов. Не мудрствуя лукаво, с каждым из лагранжианов соотносят некоторый тип квантовых объектов, частиц. Само взаимодействие описывается посредством сложения лагранжианов частиц. Взаимодействие приводит к изменению динамических характеристик частиц, в частности массы и заряда. Однако при вычислении их значений возникают бесконечно большие величины, что вызывает недоумение. Экспериментальные данные вроде бы свидетельствуют о конечном значении любого физического параметра. Естественно, физикам пришлось искать пути усмирения бесконечностей. Надо отметить, что на этом пути им удалось добиться замечательных успехов. Решающее значение приобрел концепт перенормировки. В соответствии с ним, оперируя со значениями физических параметров, следует их нормировать к экспериментально наблюдаемым величинам[1]. Это требование выглядит вполне естественным. Загадочность придает ему необходимость оперирования бесконечностями[2].
В квантовой теории поля большое значение придается методу возмущений, в соответствии с которым уравнение движения, разлагаемое по параметру связи, представляется в виде суммы степенных функций с бесконечным числом членов. Вся эта процедура напоминает разложение функции в ряд Тейлора. Если параметр связи значительно меньше единицы, то каждый последующий член ряда меньше предыдущего приблизительно в ki- раз. "Обрезая ряд", можно получить результаты, прекрасно согласующиеся с экспериментальными данными. Такова ситуация в квантовой электродинамике, где параметр связи мал: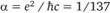 
. Если параметр связи больше или равен единице, как это имеет место в сильных взаимодействиях, то метод возмущений оказывается неэффективным. Необходимо также учитывать, что параметры связи не являются константами, они зависят от энергии взаимодействий. На это обстоятельство указывает функция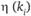
История развития концепта перенормировки применительно к любой квантово-полевой теории напоминает триллер с его остросюжетными поворотами. Героев концептуальных триллеров награждают не Оскарами, а Нобелевскими премиями. В этой связи заслуживают упоминания Ю. Швингер, С. Томонага и Р. Фейнман, которые сумели представить квантовую электродинамику уже в конце 1940-х гг. в презентабельном виде. С. Томонага сформулировал решающий вывод следующим образом. "... Все бесконечности, появляющиеся в процессах рассеяния, могут быть приписаны или бесконечности электромагнитной массы, или бесконечности заряда электрона – и никаких других бесконечностей в теории не существует. Очень приятно, что в теории нет никаких расходимостей, за исключением двух бесконечностей в массе и заряде электрона. Нельзя, конечно, утверждать, что в теории вообще нет расходимостей, поскольку масса и заряд в действительности бесконечны (курсив мой. –Прим. авт.). Однако следует заметить, что если свести бесконечности, появляющиеся в процессах рассеяния, к модификации массы и заряда, то все остающиеся члены уже будут конечными. Далее, если исследовать структуру теории, то после того как бесконечности объединены с массой и зарядом, видно, что единственными появляющимися в теории значениями массы и заряда служат величины, измененные под влиянием реакции поля; первоначальные значения и добавки, обусловленные реакциями поля, никогда не появляются по отдельности"[3]. Показательно, что в теории перенормировки на первый план выходят именно масса и заряд, т.е. две динамические характеристики.
Р. Фейнман для облегчения расчетов предложил способ графического изображения частиц, при котором взаимодействующие частицы изображаются сплошными линиями, а кванты взаимодействия – волнистыми. Их встречи называются вершинами. В амплитуду вероятности процесса дает вклад каждая из вершин, причем этот вклад пропорционален параметрам взаимодействия тех частиц, линии которых встречаются в вершине.
Ю. Швингер продемонстрировал виртуозное владение аппаратом квантово-полевых операторов. Интересно, что подходы Фейнмана и Швингера не были идентичными. Концептуальные акценты они расставляли по-разному. В отличие от Фейнмана Швингер тяготел не к корпускулярной, а к полевой интерпретации квантовой электродинамики.
Томонага, Швингер и Фейнман стали лауреатами Нобелевской премии по физике за 1965 г. "за основополагающие работы в области электродинамики". Тем не менее оставались существенные концептуальные трудности, о которых Фейнман счел нужным заявить в своей Нобелевской лекции: "Я не думаю, что у нас имеется полностью удовлетворительная квантово-механическая модель, хотя бы такая, которая не согласуется с природой, но, по крайней мере, согласуется с требованием логики о равенстве суммы вероятностей всех возможных процессов единице. Поэтому я считаю, что теория перенормировок – это просто способ спрятать под плед трудности с расходимостями в квантовой электродинамике. Но я, конечно, не уверен в этом"[4].
Многогранность науки
В физике сложилась удивительная ситуация. Р. Фейнман, гениально одаренный физик, создатель квантовой электродинамики, предложивший методы, позволившие объяснить многочисленные экспериментальные данные, тем не менее ставит под сомнение основополагающий концепт, каковым является понятие перенормировки. Это ли не свидетельство поразительной концептуальной насыщенности современной физики, а также необходимости всемерного развития ее метаисследований!
Что же представляет собой перенормировка? Интуитивный прием, непонятно каким образом приводящий к успеху, или концепт, выражающий сокровенные черты квантово-полевой теории, в данном случае электродинамики? Приведем на этот счет два толкования, принадлежащие опять же не рядовым, а выдающимся физикам. В прекрасной обзорной статье В. И. Григорьев и В. А. Ефремов утверждают, что "важная часть идеи перенормировок – указание на необходимость построения теории, в которой выступали бы не математические, а физические частицы"; "в природе нет никаких “математических” частиц, все частицы “физические”, и их должна описывать теория"[5].
Принципиально другая позиция выражена С. Томонагой в приведенной выше цитате, в которой автор выделил курсивом слова "масса и заряд в действительности бесконечны". Еще более определенно высказывается Э. Блэкмен в статье с характерным названием "Перенормировка: наш самый большой недопонятый друг": "Прежде всего, в утверждении скептиков, что электрон не обладает бесконечной массой и зарядом, содержится порок. В действительности, в соответствии с квантовой теорией поля, он обладает ими! Основание, в силу которого мы не понимаем этого, является утонченным, но красивым. Если электрон обладает бесконечным зарядом, то он воспринимает от электромагнитного поля бесконечное количество энергии. Эта энергия проявляется в соответствии с принципом неопределенности, согласно которому поле может создавать и уничтожать частицы с малым временем жизни; такие частицы называются виртуальными. При таком большом объеме энергии поле обладает способностью производить вокруг электрона много заряженных частиц. Но так как эти виртуальные частицы обладают зарядом, то они взаимодействуют с полем и ослабляют силу, по аналогии с диэлектриками в классической электродинамике. Следовательно, чем дальше от электрона, тем меньше его эффективный заряд, ибо он ослабевает из-за диэлектрического эффекта, уменьшая в результате значение заряда, которое мы измеряем"[6].
Разумеется, эффект поляризации вакуума, описанный Блэкменом, известен всем знатокам квантовой теории поля. Но, тем не менее, они не едины в своих мнениях относительно бесконечных по своему значению физических параметров. Если некоторые авторы придают им исключительно математическую значимость, то другие настаивают на их физической актуальности. В этом нетривиальном споре автор склонен согласиться с теми исследователями, которые настаивают на физической актуальности бесконечных значений. И вот почему.
В физической теории нет ничего чисто математического. Все математические концепты, будучи используемыми в интересах развития физической теории, непременно нагружаются физическим смыслом. Но как же понимать в таком случае отсутствие бесконечных значений в экспериментах? Очень просто. В соответствии с концептуальным устройством квантовой теории поля невозможно объяснить результаты экспериментов без признания бесконечных значений физических параметров. Следовательно, необходимо решиться на их признание. Как известно, цикл познания включает не только эксперимент, но и абдукцию. Именно абдукция, т.е. процесс достижения понимания законов и принципов, вынуждает признать актуальность перенормировки, а также бесконечных по величине физических параметров. Исследователи, преувеличивающие значимость эксперимента, стремятся ограничиться его данными, которые всегда конечны. Но не следует забывать об актуальности также и абдукции!
Для того чтобы осуществить перенормировку, предварительно необходимо выбрать регулирующий параметр. Обычно он соотносится с некоторой шкалой энергий элементарных частиц или же соответствующей ей шкалой пространственных и временны́х характеристик. Разработано достаточно много способов регуляризации, каждый из которых обладает своими сильными и слабыми сторонами. Показательны в этом смысле размерная регуляризация Хоофта – Велтмана и решетчатая регуляризация К. Уилсона. В первом случае вместо четырехмерного пространства-времени вводится Д-мерное пространство- время, где Д не обязательно является целым числом. Во втором случае вводится минимальный шаг пространственно-временной решетки. Можно сказать, что пространство и время считаются дискретными. В результате интегралы "обрезаются" таким образом, что исключаются бесконечные величины для значений эффективных параметров. Интересно, что подчас выбираемые регулирующие параметры эквивалентны друг другу, в таком случае они образуют ренормализационную группу.
С метанаучной точки зрения наиболее интересным является вопрос об актуальности перенормировки. Правомерно ли считать ее всего лишь приемом, лишенным глубокого концептуального содержания? Положительный ответ на этот вопрос стимулируется двумя обстоятельствами. Во-первых, регулирующий параметр сначала вводится в квантовую теорию поля, но затем, по окончании операции перенормировки, выводится из нее посредством некоторого предельного перехода, в соответствии с которым его устремляют либо к нулю, либо к бесконечности. Во-вторых, все известные способы регуляризации обладают определенными недостатками. Так, размерная регуляризация едва ли совместима с теорией суперсимметрии. Решетчатая же регуляризация нарушает Лоренц-инвариантность. В пользу отрицательного ответа на поставленный вопрос свидетельствует эффективность операции перенормировки, без которой невозможно представить себе современную квантовую теорию поля.
По мнению автора, сомнения в актуальности регуляризации неосновательны. Научные теории, в том числе квантовая теория поля, не могут быть сформулированы в виде, исключающем всякие проблемы. Решающее значение имеет не безупречная формулировка теории, а обеспечение роста научного знания. Так как и регуляризация, и перенормировка способствовали росту научного знания в квантовой теории поля, то не приходится сомневаться в их актуальности. Другое дело, что необходимо предпринять дополнительные шаги по выяснению концептуальной рафинированности перенормировки, в том числе регуляризации.
Выводы
1. Перенормировка – важнейший концепт квантовой теории поля.
2. Он обеспечивает гармонию дедукции и эксперимента (аддукции).