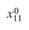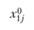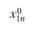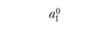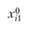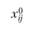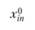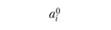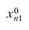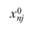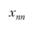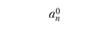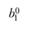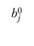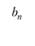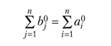Гравитационные и энтропийные модели прогнозирования передвижений

В отличие от оптимизационных задач модели, рассматриваемые в этом подпараграфе, используются не для определения наилучшего решения, а для прогнозирования наиболее вероятного массового поведения. При этом, как правило, прогнозируются транспортные потоки между населенными пунктами рассматриваемой системы расселения (или между планировочными районами, если пользоваться терминологией из области градостроительного планирования). Основные идеи этого подхода заимствованы из физики (теории гравитации и термодинамики).

Первый тип моделей данного класса – гравитационные. В. Рейли при анализе конкуренции в розничной торговле

впервые сформулировал закон взаимодействия центров тяготения, используя аналогию с законом всемирного тяготения. Согласно закону Рейли, притяжение 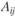, создаваемое городом i в точке j, пропорционально населению города 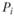и обратно квадрату расстояния 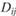. Таким образом, измеряемая в точке j сила притяжения 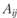со стороны города i равна

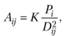(2.34)

где К – эмпирически определяемая постоянная.

В дальнейшем этот закон многократно применялся в различных странах в эмпирических экономико-географических исследованиях, приобретая новые формулировки. В качестве меры значения города не обязательно брать население. В зависимости от содержания задачи исследования могут браться и другие характеристики. Например, при изучении влияния торговли можно использовать торговый оборот или размер территории, на которой осуществляется торговля. Также не обязательно, чтобы показатель степени при переменной расстояния был равен 2 (так как этот показатель просто заимствован из закона всемирного тяготения).

При изучении передвижений закон Рейли можно представить в следующем более общем виде:

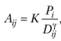(2.35)

где параметр γ характеризует транспортную проницаемость (доступность) территории.

Расстояние можно заменить другими показателями доступности: временем, затрачиваемым на поездку, стоимостью поездки и другими характеристиками издержек передвижения.

Рассмотрим два населенных пункта, между которыми осуществляется экономическое взаимодействие (в частности, это могут быть маятниковые трудовые миграции). Число передвижений 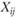между пунктами i и j пропорционально "тяготению" со стороны j (т.е. числу рабочих мест 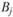в задаче о трудовых миграциях), "массе" пункта i (численность работающего населения 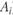), а также зависит от доступности корреспонденций между i и j:

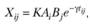(2.36)

где 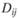– расстояние между i и j, 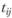– затраты времени на поездку из i в j; 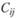– стоимость поездки; f – функция транспортной доступности. Эта функция может иметь различный вид. Наиболее часто используются степенная и экспоненциальная функции. В первом случае используется Вперед формула:

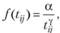(2.38)

где 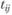– время на поездку из i в j; параметр расселения 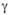– показатель влияния фактора доступности на трудовые корреспонденции (представляет собой конкретизацию для данной задачи параметра транспортной проницаемости территории в рассмотренной выше формуле (2.35)); а – коэффициент пропорциональности.

Во втором случае доступность f выражается формулой:

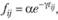(2.39)

где параметры а и γ имеют тот же смысл, что и в первом случае.

На практике используются более сложные варианты этих формул для учета поведения различных групп населения, различных типов поездок и пр.

Отметим, что эмпирические исследования распределений населения по затратам времени на передвижения с трудовыми целями (а также при совершении других типов поездок) выявили, что функции распределения являются экспоненциальными, что свидетельствует в пользу выбора экспоненциальной функции доступности.

Таким образом, для оценки трудовых корреспонденций (поездок с трудовыми целями) между населенными пунктами i и j может использоваться Вперед формула:

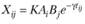(2.40)

где параметр расселения γ подбирается на основе транспортных социологических обследований, а К – коэффициент пропорциональности.

Рассматривая два населенных пункта, между которыми осуществляется экономическое взаимодействие (в частности, маятниковые трудовые миграции), увидим, что если необходимо составить прогноз величины транспортного потока между пунктами i и j при заданных величинах изменения численности населения (или числа занятых), а также, возможно, при изменении затрат, связанных с передвижениями (из-за развития транспортных средств и транспортных сетей), то при использовании формулы (2.40) на первом этапе происходит ее калибровка по наблюдаемым данным, т.е. при наблюдаемых значениях 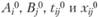определяются параметры и k, обеспечивающие выполнение равенства (2.40).

На втором этапе для планируемых значени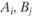й и 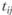(например, при разработке генерального плана муниципального района, городского округа или территориальной схемы развития субъекта федерации) определяется ожидаемая величина 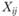при предположении, что параметры γ и k остаются неизменными.

Такое решение не будет оптимальным с точки зрения минимизации транспортных издержек в рамках решения транспортной задачи (как это рассматривалось в подпараграфе 2.4.1), но будет отражать сложившиеся предпочтения населения, среди которых транспортные издержки являются не единственным и, возможно, даже не определяющим фактором. Стабильность параметров γ и k определяется во многом сложившимся образом жизни, предпочтениями жителей и другими плохо формализуемыми факторами, от которых зависит мобильность населения (или рабочей силы).

Обобщением данного подхода являются энтропийные модели прогноза передвижений, заимствованные из термодинамики.

Рассмотрим систему расселения, состоящую из п планировочных районов (это могут быть города и поселки, находящиеся друг от друга на расстоянии, позволяющем совершать ежедневные поездки, или же это могут быть районы крупного города или городской агломерации, включая пригороды). Ограничим пример рассмотрением только трудовых корреспонденций (т.е. поездок, совершаемых работающим населением с трудовыми целями), хотя модель имеет модификации для учета и других видов поездок.

Пусть 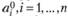– численность работающего населения района 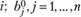– число рабочих мест в районе j; – матрица затрат времени (или денег) на передвижения из одного района (i) в другой (j), при имеющемся на момент наблюдения уровне развития транспортной системы.

Проведение транспортного обследования позволяет также составить матрицу 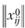, отражающую наблюдаемое распределение потоков трудовых корреспонденций между планировочными районами.

Таким образом, на момент начала разработки прогноза наблюдается Вперед система передвижений с трудовыми целями внутри рассматриваемой системы расселения (табл. 2.9).

Таблица 2.9

Матрица трудовых корреспонденций для системы расселения, включающей п планировочных районов

№ района	1		j		N	Численность работающего населения района
1		…		…
…	…	…	…	…	…	…
I		…		…
	…	…	…	…	…	…
N		…		…
Число рабочих мест района		…		…

В этой матрице выполняются равенства:

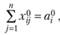(2.41)

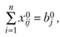(2.42)

т.е. считается известным для каждой пары районов i и j, сколько жителей района i ежедневно отправляется на работу в район j. Задача состоит в том, чтобы для заданных на конец планового периода новых значени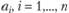й и 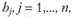а также при новых значениях затрат времени (денег) на передвижения , найти ожидаемую (наиболее вероятную) матрицу , т.е. составить прогноз трудовых корреспонденций между планировочными районами.

Прежде всего отметим, что наблюдаемая матрица при заданных значениях затрат времени 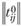позволяет построить распределение работающего населения по затратам времени на поездки с трудовыми целями. Как показали многочисленные транспортные обследования, эта функция является экспоненциальной.

Таким образом, хотя большая часть работающих граждан стремится работать в непосредственной близости от дома, для некоторых этот фактор не является определяющим. Для части работающего населения выбор места жительства определяется семейными обстоятельствами (например, доступность рабочих мест для других членов семьи), а также иными факторами (например, если работа не требует ежедневных поездок). Таким образом, распределение населения по времени поездок с трудовыми целями задается формулой

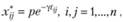(2.43)

где γ – параметр расселения (аналогичен параметру транспортной доступности в формуле (2.35)); 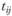– средние затраты времени на передвижения из района i в район j; р – коэффициент, обеспечивающий выполнение условия:

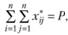(2.44)

где Р – общая численность работающего населения территориальной системы.

Матрица , называется матрицей априорных предпочтений. Она показывает не только распределение транспортных потоков, но и распределения рабочих мест и жителей между районами, которые соответствуют предпочтениям жителей относительно расселения и системы передвижений. Ключевым элементом этой матрицы является коэффициент γ, обладающий, как показали исследования, большой устойчивостью. Он тесно связан со средними для территориальной системы затратами времени на трудовые корреспонденции и определяется бюджетом времени работающего населения. Для работающего населения крупных городских агломераций средние затраты времени на поездки с трудовыми целями составляют, как правило, около 40 мин (в одну сторону). При развитии транспортной системы и совершенствовании средств транспорта границы агломерации расширяются, по средние затраты времени на передвижения и, соответственно, коэффициент γ, практически не изменяются.

Возвращаясь к формуле (2.43) отметим, что коэффициент р после определения параметра γ вычисляется по формуле

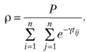(2.45)

поскольку матрица 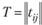является заданной.

Если параметр 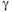определен (по наблюдаемой на начало прогнозного периода матрице трудовых корреспонденций), то прогноз передвижений работающего населения между районами с трудовыми целями на конец прогнозного периода приновых (плановых) значениях параметров 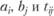, где сводится к решению задачи максимизации энтропии при заданных ограничениях:

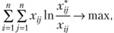(2.46)

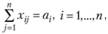(2.47)

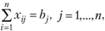(2.48)

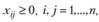(2.49)

где 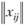– искомая матрица трудовых корреспонденций; 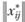– матрица априорных предпочтений; планируемая численность работающего населения планировочного района i к концу рассматриваемого периода; 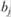, 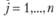– планируемая численность рабочих мест в районе j к концу рассматриваемого периода.

Можно доказать, что решение данной задачи достигается методом "балансировки невязок", т.е. последовательным пересчетом элементов матрицы 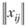, по формулам:

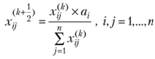(2.50)

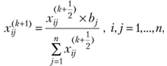(2.51)

где k – номер итерации.

На первом шаге решения рассматривается матрица априорных предпочтений 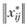. Суммы 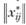по строкам будут, как правило, отличаться от плановых значений а„ а по столбцам – от плановых значений bj хотя

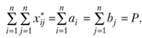(2.52)

где Р – численность работающего населения территориальной системы, равная числу рабочих мест. Возникают так называемые невязки, хорошо известные в бухгалтерском учете при составлении балансов, т.е. величины и 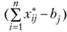как правило, не равны нулю. Эта разница 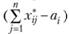"разгоняется по балансу" с помощью формул (2.50, 2.51). При пересчете элементов матрицы 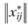по формуле (2.50) достигается выполнение ограничений (2.47). Полученные новые значения элементов матрицы пересчитываются по формуле (2.51) для выполнения условий (2.48). Этим завершается первая итерация решения. Условия (2.47) для новой матрицы опять не выполняются, но величина "невязок" уменьшилась. Процесс продолжается до тех пор, пока условия (2.47) и (2.48) не будут выполняться с заданным уровнем точности.

Доказано, что последовательным применением формул (2.50, 2.51) задача (2.46–2.49) всегда может быть решена с любой степенью точности. Полученный в результате прогноз трудовых корреспонденций показывает, как распределятся передвижения с трудовыми целями работающего населения территориальной системы (при заданных плановых значениях 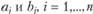) после достижения системой равновесного состоя́ния, т.е. после того, как пройдут цепочки обменов жилья и смен мест работы, позволяющие работающим гражданам максимально приблизиться к априорным предпочтениям 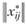, после изменений числа рабочих мест и численности работающих для каждого района, а также изменений затрат времени на передвижения .

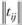Приведенный алгоритм решения задачи (2.46–2.49) является громоздким в вычислительном отношении. На практике, как правило, используется более эффективный модифицированный метод балансировок, основанный на вычислении оптимального решения двойственной задачи.

Как показал А. Дж. Вильсон, при определенных соотношениях между параметром расселения γ и средним временем в расчете на одного работающего, затрачиваемым на передвижения с трудовыми целями (в одну сторону) 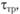задача (2.46–2.49) эквивалентна следующей задаче:

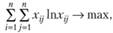(2.53)

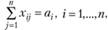(2.54)

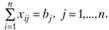(2.55)

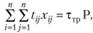(2.56)

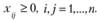(2.57)

Таким образом, вместо матрицы априорных предпочтений в энтропийных задачах прогнозирования передвижений может использоваться параметр 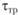– среднее время поездки заданного назначения (например, поездки типа "дом – работа") для рассматриваемой территориальной системы.

Вернемся к задаче (2.46–2.49). Как было отмечено выше, для ее решения используются двойственные оценки. Двойственные оценки 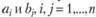связаны с переменными задачи (2.46–2.49) 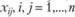следующими соотношениями:

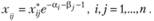(2.58)

Оценки 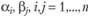: характеризуют эффективность размещения в каждом из планировочных районов дополнительно одного места расселения 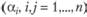или одного рабочего места 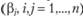i с точки зрения приближения затрат времени на передвижения в системе к априорным предпочтениям населения.

Для оценки относительной нехватки или избытка мест расселения или рабочих мест в каждом районе используются функциональные градостроительные оценки, основанные на вычислении градиента 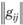целевой функции (2.46) в точке оптимума 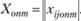, Можно показать, что градиент будет равен:

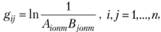(2.59)

где 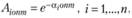(2.60)

(2.61)

Или, после упрощения выражения: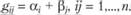

Тогда относительная нехватка или избыток жилья в районе 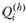при заданном ограничением (2.48) распределении рабочих мест по районам оценивается по следующей формуле:

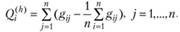(2.62)

Аналогично относительная нехватка или избыток рабочих мест в районе 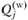при заданном ограничением (2.47) распределении численности работающего населения по районам составит:

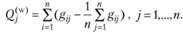(2.63)

Оценки 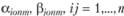и построенные на их основе оценки 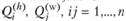характеризуют спрос на жилье и рабочие места со стороны населения и могут рассматриваться в качестве одного из факторов формирования цен на землю, объемов строительства жилья и размещения предприятий по районам территориальной системы.

Задача (2.53–2.57) эквивалентна задаче (2.46–2.49) при определенных соотношениях параметров 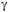и 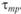/ В этом случае переменные 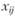и двойственные оценк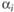и и 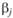связаны между собой соотношением:

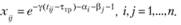(2.64)

Значения и интерпретация оценок для задачи вида (2.53–2.57) остаются теми же, что и для задачи (2.46–2.49).

Рассмотрим модификацию задачи (2.46–2.49), в которой некоторые ограничения заданы в виде неравенств. Пусть, например, ограничение (2.47) имеет вид:

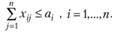(2.65)

Модели данного типа предназначены уже не для прогнозирования передвижений населения при заданном варианте развития территориальной системы, а для планирования жилищного строительства в каждом из планировочных районов при заданных градостроительных ограничениях. Исходя из содержания модели, спрос на жилье определяется исключительно априорными предпочтениями работающего населения относительно затрат времени на передвижения с трудовыми целями. Однако если вспомнить, как определяется матрица априорных предпочтений 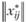(или среднее время передвижений 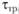), то станет ясно, что используемый при этом параметр расселения неявно включает в модель все прочие факторы, заставляющие людей выбирать место работы или жилье, удаленные друг от друга на то или иное расстояние. Добавление в модель передвижений с другими целями (посещение магазинов, рекреация и пр.), а также включение в рассмотрение передвижений неработающего населения, позволяют еще более приблизить модель к реальной ситуации.

Аналогично можно планировать изменение числа рабочих мест в каждом районе, заменив ограничение (2.48) в модели (2.46-2.49) на

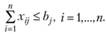(2.66)

Доказано, что задачи такого типа, а также задачи, в которых некоторые ограничения заданы и сверху, и снизу (например: 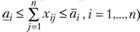, имеют решение, алгоритм поиска которого основан на рассмотренных выше принципах, хотя и является более громоздким.

При использовании энтропийных моделей в задачах территориального планирования, помимо отмеченного выше учета передвижений с различными целями, вводятся также дополнительные параметры и ограничения для моделирования различий в передвижениях разных групп населения, а также для учета различных видов транспорта и зависимости времени передвижения от величины транспортного потока.

Подобного рода модели использовались для обоснования решений относительно развития транспортной системы при разработке Генерального плана Ленинграда и Ленинградской области в 1987 г. и Генерального плана Санкт-Петербурга в 2005 г. Несколько иные модификации базовой модели использовались также при расчете оценок земельных ресурсов по функционально-экономическим зонам Санкт-Петербурга для дифференциации ставок платы за землю, устанавливаемых землепользователям города.