Гипотетико-дедуктивный метод и его логическая структура

Поскольку общий принцип обоснования индукции так и не был найден, на смену индуктивной модели к 1930-м гг. пришла гипотетико-дедуктивная модель. Эта модель широко распространилась в среде сторонников логического позитивизма (неопозитивизма), которые ограничивали задачу философии науки логическим анализом существующего знания.

Вместе с тем форму гипотетико-дедуктивных рассуждений можно обнаружить еще у мыслителей античной Греции. Эти рассуждения использовались как в публичной полемике, так и при обучении риторике или эристике (искусству спора).

Метод критического рассуждения составил основу античной диалектики (от древнегреч. dialektike techne – вести диалог, беседу, полемику), как искусства поиска истины путем раскрытия противоречий в мышлении. В ходе такого диалога один из его участников выдвигает определенные предположения или мнения, а другой участник оспаривает, критикует или опровергает их.

В итоге участники диалога либо приходят к установлению истины, либо выясняют, в чем их мнения сходны и в чем эти мнения расходятся.

Блестящим мастером проведения диалогов по нравственным и общественно-политическим проблемам был Сократ. О мастерстве последнего можно судить по сочинениям Платона, написанным в форме диалогов, непременным участником которых выступает Сократ. Платон утверждал, что истина не может быть в противоречии с самой собой, и надо отвергать такие гипотезы, которые приводят к противоречию. По Платону, диалектика есть точный метод доказательства, и в его диалогах не встречается иного метода доказательства, кроме опровержения гипотез.

Современная культура использует гипотетико-дедуктивные рассуждения в процессе обучения. Наибольшее распространение эти рассуждения получили в разнообразных спорах, дискуссиях, полемике. Речь идет как о состязании сторон в судебных заседаниях, так и о научных дискуссиях и диспутах.

Особая роль гипотетико-дедуктивного метода в науке проявилась в связи с возникновением экспериментального естествознания. Так, ярким примером гипотетико-дедуктивных систем стала классическая механика Ньютона, в основе которой лежат гипотезы, опирающиеся на огромное число наблюдений и экспериментов, проверенных опытом и практикой.

Аксиомы абстрактных математических теорий не допускают непосредственной эмпирической проверки, поэтому при выборе математических аксиом руководствуются требованиями внутренней логики развития теории.

Наглядный пример такой логики – исследования великого русского математика Н. И. Лобачевского (1792–1856). Многие столетия математики безуспешно пытались доказать евклидову аксиому о параллельных прямых: "Через данную точку к прямой на плоскости можно провести лишь одну прямую, параллельную данной". Попытки Н. И. Лобачевского на этом направлении также были безуспешны. Тогда математик попытался доказать эту аксиому апагогическим методом, т.е. "от противного". Он решил заменить постулат Евклида противоположным постулатом и построить на этой основе новую геометрию, надеясь, что обнаружившиеся в процессе построения противоречия покажут несостоятельность этого нового постулата и докажут справедливость постулата Евклида.

Н. И. Лобачевский ввел аксиому: "Через данную точку к прямой на плоскости можно провести, по крайней мере, две прямые, параллельные данной" и из новой системы аксиом получил такие следствия, которые, хотя и противоречили повседневным пространственным представлениям, с позиций языка математики оказались логически непротиворечивыми. Так, в геометрии Евклида сумма внутренних углов треугольника равна 180°, в геометрии Н. И. Лобачевского – меньше этой величины. Впоследствии были построены другие системы неевклидовых геометрий. Какая из этих геометрий наиболее адекватно описывает реальное пространство – вопрос физики как эмпирической науки, но отнюдь не математики.

Г. И. Рузавин подчеркивает: "На этом примере мы убеждаемся в том, что абстрактная теория может быть логически непротиворечивой, но не обязательно применимой для описания реального мира. Чтобы убедиться в этом, мы должны абстрактным понятиям геометрии дать определенную интерпретацию. Так, прямую линию можно интерпретировать как путь светового луча, а точку – как пересечение таких лучей. После этого следует проверить экспериментальными методами, в какой мере ее теоремы выполняются в мире физического опыта".

Таким образом, в математике гипотетико-дедуктивный метод используется прежде всего при проверке ее теорий. Что касается эмпирических наук, то они используют этот метод для построения своих теорий. Система обобщений и гипотез организуется таким образом, чтобы менее общие гипотезы можно было бы логически вывести из более общих гипотез.

Гипотетико-дедуктивный метод в наибольшей мере используется в тех отраслях естествознания, где разработан концептуальный аппарат и широко применяются математические методы исследования, в том числе в экономических теориях.

В описательных науках, где связь гипотез достаточно поверхностна, применение этого метода затруднительно, поскольку: во-первых, трудно найти и выделить основные, наиболее сильные гипотезы, из которых можно было бы с помощью логической дедукции получить другие гипотезы; во-вторых, вследствие этого нелегко выявить не основные, производные гипотезы; в-третьих, само число гипотез бывает весьма велико.

Так, характеризуя состояние современной ему этнографии, Л. Н. Гумилев (1912–1992) указывал, например: в ней "количество фактов столь многочисленно, что речь идет не об их пополнении, а об отборе тех, которые имеют отношение к делу... Количество сведений росло, но в новое качество не переходило".

В процессе перехода от описательной науки к науке теоретической (процесс, характерный для современной теории социальной работы) существенно возрастает роль дедукции в процессе систематизации гипотез и создания целостной теории.

Общая структура гипотетико-дедуктивного метода включает в себя следующие шаги его реализации:

а) ознакомление с фактическим материалом, требующим теоретического объяснения и попытка такового (которая не достигает успеха в силу недостаточности имеющихся знаний) с помощью уже существующих теорий и законов;

б) выдвижение гипотезы о причинах и закономерностях данных явлений;

в) оценка основательности и серьезности гипотез и отбор из их множества наиболее вероятной гипотезы;

г) выведение из гипотезы следствий с уточнением ее содержания;

д) экспериментальная проверка выведенных из гипотезы следствий.

Гипотеза либо получает экспериментальное подтверждение, либо опровергается. Вместе с тем подтверждение отдельных следствий не гарантирует ее истинности (или ложности) в целом. Лучшая по результатам проверки гипотеза переходит в теорию.

Гипотетико-дедуктивный метод в естествознании. В процессе становления любой науки накопление и систематизация эмпирической информации занимает значительный период времени. Например, в естествознании процесс теоретического осмысления и установления логической связи между накопленными эмпирическими фактами посредством гипотетико-дедуктивного метода начался только в XVII в.

Так, Г. Галилей прибегал к этому методу при анализе равноускоренного движения. Частным случаем равноускоренного движения является свободное падение тел под действием силы тяготения (в терминологии Г. Галилея – "местное движение"). В книге "Беседы и математические доказательства двух новых отраслей науки, относящихся к механике и местному движению" Г. Галилей специально рассматривает метод, с помощью которого он пришел к установлению закона постоянства ускорения свободно падающих тел вблизи земной поверхности. Книга построена как шестидневные беседы между четырьмя собеседниками, которые на третий день беседуют о местном движении.

Г. И. Рузавин предлагает реконструкцию размышлений Г. Галилея, опирающихся на использование гипотетико-дедуктивного метода. Эта реконструкция выглядит следующим образом.

В современных математических терминах галилеевский закон можно записать в виде следующего дифференциального уравнения:

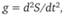
где g – ускорение свободного падения; S – путь; t – время.

Интегрируя это уравнение, устанавливаем, что скорость падающего тела пропорциональна времени падения:

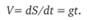
Вначале Г. Галилей, как и его предшественники (Леонардо да Винчи, Д. Бенедетти и др.), полагал, что скорость падения пропорциональна пройденному пути. Впоследствии он был вынужден отказаться от этой гипотезы, поскольку следствия из нее не подтверждаются опытом.

Подтверждалась данными опыта другая гипотеза: скорость пропорциональна времени падения.

Эта гипотеза приводит к следствию: путь, пройденный падающим телом, пропорционален квадрату времени падения, и это следствие хорошо подтверждается данными опыта.

Реконструируя ход рассуждений, Г. Галилей, как можно предположить, анализировал последовательный ряд гипотез.

Гипотеза 1:

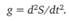
Из данной гипотезы интегрированием получается гипотеза 2-го уровня: скорость падающего тела пропорциональна времени падения.

Гипотеза 2:

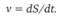
Последовательным интегрированием из этой гипотезы получают гипотезу 3-го уровня: путь, пройденный падающим телом, пропорционален квадрату времени падения:

Гипотеза 3:

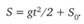
Из гипотезы 3 можно получить неограниченное число частных случаев, рассматривая путь свободного падения (в метрах) за одну, две, три и т.д. секунды, с учетом, что g = 9,8:

Гипотеза 4 (время – 1с):

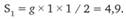
Гипотеза 5 (время – 2 с):

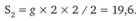
Гипотеза 6 (время – 3 с):

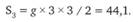
Все перечисленные гипотезы имеют низший уровень абстрактности и поэтому их можно непосредственно проверить на опыте.

Так, гипотезы 4–6 непосредственно проверяются на опыте. В свою очередь, они подтверждают гипотезу 3. Гипотеза 3 подтверждает гипотезу 2, которая, в свою очередь, аргументированно подтверждает гипотезу 1.

Именно подтверждение опытом гипотез низшего уровня заставило Г. Галилея поверить в гипотезу высшего уровня.

Рассуждения Г. Галилея представляют собой сравнительно простую гипотетико-дедуктивную систему, в рамках которой каждая из последовательно рассматриваемых гипотез имеет более низкий уровень абстрактности, чем Назад и поэтому может быть выведена из предыдущей с помощью логико-математических методов.

Существенно, что эта система гипотез строится таким образом, чтобы обеспечить проверку гипотез самого низкого уровня непосредственно на опыте. Такая проверка производится путем эмпирических измерений переменных величин, фигурирующих в гипотезе.

В сочинениях Г. Галилея можно встретить и другие простые примеры гипотетико-дедуктивных систем, состоящих из трехчетырех гипотез соответствующего уровня. Реконструкция логических размышлений Г. Галилея позволяет наглядно показать принципиальное отличие логической направленности классической дедукции от гипотетико-дедуктивного метода.

Направленность логического вывода в классической дедукции – от общего к частному. Иными словами, общее положение уже известно, на этом основании надо выявить характеристики частного знания.

Направленность логического вывода в гипотетико-дедуктивном методе противоположна – от частного к общему. Известны конкретные факты, и обосновано (т.е. считается истинным) частное знание об этих фактах. На этом основании надо подтвердить общее знание, которое носит лишь гипотетический, в некоторой мере правдоподобный характер. Иными словами, строится достаточно сложная логически связанная цепочка рассуждений, посредством которой известными фактами подтверждается истинность гипотезы самого высокого уровня.

Значение гипотетико-дедуктивного метода при построении научного знания в развивающихся отраслях естествознания определяется тем, что здесь речь идет не просто о дедуктивной связи нескольких гипотез, а о целой системе предположений, допущений, обобщений, эмпирических и теоретических законов и принципов.

Г. И. Рузавин показывает, что "любые теоретические утверждения и системы в опытных и фактуальных науках, начиная от эмпирических утверждений и кончая теориями, представляют собой гипотезы. Поскольку они рассматриваются не обособленно, а в логической взаимосвязи друг с другом, постольку степень их правдоподобия бывает настолько высока, что приближается к практической достоверности. Именно поэтому, например, законы классической механики на протяжении двух столетий казались незыблемыми, абсолютными законами природы. Такой характер придала им гипотетико-дедуктивная система, созданная для механики И. Ньютоном".

В знаменитых "Математических началах натуральной философии" И. Ньютон начинает изложение своей системы с определения исходных понятий механики и трех основных законов движения. Важнейшим из них служит 2-й закон, устанавливающий, что "изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует". Из трех основных законов механики Ньютона можно вывести ранее открытый Галилеем закон свободного падения, а если добавить к этим законам и закон всемирного тяготения, то из этой системы законов можно вывести закон Кеплера о движении планет.

Роль И. Ньютона в разработке гипотетико-дедуктивного метода и построении на его основе классической механики трудно переоценить. Часто вклад И. Ньютона в развитие гипотетико-дедуктивного метода сопоставляют с научными достижениями Евклида, применившего аксиоматический метод для построения элементарной геометрии. Ньютоновский метод фактически выступает как метод исходных начал. "Вывести два или три общих начала движения из явлений и после этого изложить, каким образом свойства и действия всех телесных вещей вытекают из этих явных начал, – было бы очень важным шагом в философии, хотя бы причины этих начал и не были еще открыты".

Поиск такого рода первоначал (или принципов) предполагает широкое использование гипотез самого различного характера. Однако в литературе по истории и методологии науки нередко утверждается, что И. Ньютон был противником использования гипотез в науке, при этом ссылаются на его заявление: "Гипотез не измышляю" ("Hypotheses поп fingo").

На самом деле тезис И. Ньютона продиктован его последовательной борьбой со схоластической метафизикой, часто изобретавшей самые фантастические, умозрительные и произвольные гипотезы, которые были тогда широко распространены. Собственные гипотезы И. Ньютон выдвигал, опираясь на достоверные факты и на тщательную проверку измерениями следствий из них. Примером может служить история открытия закона всемирного тяготения: гипотезу о том, что тела падают на Землю и Луна движется вокруг Земли под действием одной и той же силы, И. Ньютон неоднократно проверял вычислениями, используя результаты заслуживающих доверия точных экспериментальных измерений важнейших параметров движения Луны и падения тел на Земле.

Приходилось И. Ньютону бороться и против приписывания предметам и явлениям так называемых скрытых качеств для объяснения реальных явлений природы. Так, сущность электрических явлений (как проявлений статического электричества) объяснялась действием "электрической силы", сущность тепловых явлений – действием "теплорода", или тепловой жидкости и др. По И. Ньютону, такие "объяснения" лишь затемняют процесс познания природы, поэтому для него исходные принципы науки – это не утверждения о "скрытых качествах", а "общие законы природы, согласно которым образованы все вещи".

Тем не менее, как отмечал С. И. Вавилов, И. Ньютон неоднократно использовал метод выдвижения и проверки гипотез, соблюдая при этом должную осторожность.

И. Ньютон подчеркивал, что следует принимать такие гипотезы, которые не противоречат опыту и другим достоверным истинам: "И хотя аргументация на основании опытов и наблюдений посредством индукции не является доказательством общих заключений, однако это – лучший путь аргументации, допускаемый природой вещей, и может считаться тем более сильным, чем обще́е индукция... Путем такого анализа мы можем переходить от соединений к ингредиентам, от движений – к силам, их производящим, и вообще от действий к причинам, от частных причин к более общим, пока аргумент не закончится наиболее общей причиной".

Метод принципов (так назвал его С. И. Вавилов) И. Ньютона фактически был доминирующим в XVIII–XIX вв. А. Эйнштейн в книге "Физика и реальность" отмечал: большинство физиков того времени полагали, что основные понятия и принципы теорий получаются из данных опыта с помощью "абстракции", т.е. логическим путем. Ясное понимание неверности такого представления дала, как считает А. Эйнштейн, только общая теория относительности: "Она показала, что, опираясь на фундамент, значительно отличающийся от ньютоновского, можно объяснить соответствующий круг экспериментальных данных более удовлетворительным образом, чем опираясь на фундамент, взятый Ньютоном".

То, что можно указать две принципиально различные теоретические основы, которые одинаково хорошо согласуются с опытными данными, как раз и свидетельствует, как полагает А. Эйнштейн, об умозрительном характере основных положений теории. Такой взгляд на природу теоретических принципов все больше распространяется среди ученых по мере того, как возрастает зазор между понятиями и принципами, с одной стороны, и опытными данными – с другой. Важной закономерностью развития физического знания А. Эйнштейн считает то, что "путь от теории к наблюдению становится длиннее, тоньше и сложнее". В связи с этим, по его мнению, "теория вынуждена переходить все более и более от индуктивного метода к дедуктивному".

Таким образом, любая теоретическая система опытного знания оказывается тем более ценной, чем больше она позволяет получить логических следствий, которые оказываются доступными для опытной проверки. Ранее исключительной сферой приложения индуктивного метода считались опытные науки. Однако развитие науки показало, что для эмпирического знания дедукция служит не только средством объединения и систематизации результатов эмпирического исследования, но и поиска и обоснования наиболее общих и глубоких теоретических законов.

По отношению к такой развитой и теоретически зрелой науке, как физика, эта роль была подчеркнута А. Эйнштейном: "Законченная система теоретической физики состоит из понятий, основных принципов, относящихся к этим понятиям, и следствий, выведенных из них путем логической дедукции. Именно эти следствия должны соответствовать нашим опытам; их логический вывод занимает в теоретическом труде почти все страницы".

Таким образом, А. Эйнштейн показывает связи элементов в системе: понятия – основные принципы – следствия из принципов – опыты. Основную задачу ученых А. Эйнштейн видит в отыскании общих принципов, из которых путем чистой дедукции можно получить картину мира. К общим принципам ведет не логический путь, но основанная на проникновении в суть опыта интуиция. Не существует никакого индуктивного метода, который мог бы вести к фундаментальным понятиям физики.