Факторные модели, арбитражная теория ценообразования
Назначение факторных моделей – предоставить управляющему портфелем модель расчета характеристик портфеля, которая:
■ содержит существенно меньше параметров, чем общая модель Марковица;
■ достаточно хорошо объясняет изменчивость доходностей используемых активов через один или несколько (небольшое число) факторов с ясным экономическим смыслом.
Исторически первой такой моделью стала рыночная модель Шарпа, тесно связанная с САРМ.
Уравнение модели:

где k – номер актива; в качестве rм, как и в САРМ, на практике используется значение рыночного индекса.
Предположения модели:

Таким образом, остатки εk модели для различных активов предполагаются не связанными ни друг с другом, ни с колебаниями рынка.
Следствия:


Доходность и риск произвольного портфеля в рыночной модели получаются подстановкой этих величин в соответствующие соотношения модели Марковица, что дает:


Рыночная модель позволяет отчетливо понять эффект диверсификации: при m→∞ и хk→0 доходность и рыночный риск усредняются, а собственный риск стремится к нулю. Последнее обстоятельство следует из того, что собственный риск есть сумма т слагаемых, в каждом из которых стоит множитель  порядка 1 /т2.
порядка 1 /т2.
Схематично эффект диверсификации представлен на рис. 11.7.

Рис. 11.7. Эффект диверсификации
Рыночная модель Шарпа – частный случай однофакторной модели, где в качестве фактора взята доходность на рыночный индекс.
Уравнения факторной модели общего вида:
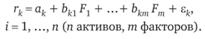
Предположения модели:

Тогда ожидаемые доходности, риски и ковариации бумаг вычисляются по формулам:

где первое слагаемое – так называемый факторный риск; второе слагаемое – нефакторный риск;

Затем для произвольного портфеля производится их подстановка в соответствующие соотношения модели Марковица.
Итак, общая схема построения факторной модели:
1) из содержательных соображений выбираются факторы;
2) по статистическим или прогнозным данным методом множественной линейной регрессии вычисляются константы аk и чувствительности bk;
3) оцениваются дисперсии и корреляции остатков εk, их корреляции с факторами, коэффициенты детерминации;
4) в случае если модель признана неудовлетворительной, повторяются шаги 1–3;
5) если требуется, рассчитывается оптимальный портфель.
Примеры выбора факторов в факторной модели:
■ Фама, Френч – индекс рынка; разность индексов доходностей больших и малых компаний; разность индексов доходностей компаний с большим и маленьким отношением балансовой стоимости к рыночной;
■ Чен, Ролл, Росс – темп промышленного роста; непредвиденная (unexpected) инфляция; разница доходностей между долгосрочными и краткосрочными облигациями; разница между доходностью государственных облигаций и облигаций инвестиционного класса;
■ Salomon Broth. – уровень инфляции, темп роста ВНП, уровень процентных ставок, изменение цены на нефть, темп роста расходов на оборону.
Как и САРМ, факторные модели содержат в себе инструмент для оценки активов и портфелей. Этим инструментом является понятие факторного арбитража. Под арбитражем в теории финансов понимается любая возможность получения прибыли без риска и при нулевых затратах. Наиболее известным видом арбитража является заключение двух противоположных сделок с одним активом. Однако арбитражная сделка может быть устроена сложнее и включать большее число позиций.
Пример 11.6
"Портфельный" арбитраж:
|
Акции |
Текущая цена |
Будущая цена |
|
|
сценарий 1 |
сценарий 2 |
||
|
А |
70 |
50 |
100 |
|
В |
60 |
30 |
120 |
|
С |
80 |
38 |
112 |
Можно заметить, что портфель из акций А, В с долями хл = 0,4, хв = 0,6 в обоих сценариях имеет такие же выплаты, как и акция С. Сценарий 1:
0,4 • 50 + 0,6 • 30 = 38.
Сценарий 2:
0,4 • 100 + 0,6 • 120=112.
Текущая стоимость портфеля равна: 0,4 • 70 + 0,6 • 60 = 64.
Его покупка в сочетании с короткой позицией по С является арбитражной сделкой. При непосредственном взгляде на таблицу возможность арбитража не является очевидной. В реальных ситуациях, с большим числом задействованных активов, для распознавания арбитражных ситуаций требуются специальные методы.
В развитой в работах Ролла и Росса (1976) арбитражной теории ценообразования (APT) используется специальное понятие факторного, или асимптотического, арбитража: в условиях принятой факторной модели под арбитражным портфелем понимается портфель, имеющий:
1) нулевую начальную стоимость;
2) нулевую чувствительность к каждому из факторов (и, следовательно, нулевой факторный риск);
3) положительную ожидаемую доходность.
Таким образом, арбитражный в смысле APT портфель может нести риск, но этот риск может быть только нефакторным. Сохранение термина "арбитраж" связано с тем, что здесь неявно используется свойство диверсифицированных портфелей иметь незначительный нефакторный риск (это свойство было проиллюстрировано для рыночной модели Шарпа и сохраняется во всех факторных моделях).
Пример 11.7
Факторный арбитраж для однофакторной модели:
|
Акция |
Чувствительность к фактору |
Ожидаемая доходность, % |
|
А |
0,8 |
15 |
|
В |
1,2 |
22 |
|
С |
0,6 |
12 |
Портфель с долями: хА = –0,3; xв = 0,1; хс = 0,2 является арбитражным.
Основное положение APT: при равновесных ценах арбитражный портфель невозможен.
Применение средств линейной алгебры позволяет установить условие отсутствия арбитража: должны существовать константы λ0, λ1, ..., λт, такие, что

Количество уравнений равно количеству активов, а количество переменных равно количеству факторов плюс один. Условие является достаточно сильным, так как обычно п много больше т. Реально на рынке всегда присутствуют отклонения от условия отсутствия арбитража. Если такие отклонения становятся значительными, в рамках APT это является сигналом для корректировки портфеля инвестора путем добавления к нему арбитражного портфеля. В результате такой корректировки стоимость и факторный риск портфеля не меняются, а его ожидаемая доходность возрастает.
Согласование САРМ и APT. Хотя APT была выдвинута как альтернатива САРМ, две модели не противоречат друг другу, что можно проиллюстрировать на примере рыночной модели Шарпа:

Мы видим, что с точностью до обозначений условие отсутствия арбитража совпадает с уравнением SML.