Эволюция методов и моделей логистики
Выполненные обобщения дисциплин научной базы логистики позволяют схематично представить методы, используемые в логистике и управлении цепями поставок, в виде рис. 3.5.
Следует подчеркнуть, что представленные на рис. 3.5 методы и модели логистики и ряд других появились достаточно давно. В период с конца XIX в. до 1960-х гг. происходило развитие наук, которые заложили основы будущей методологии логистики. Именно тогда появились статьи Ф. Харриса, Р. Уилсона, Е. Тафта, К. Стефанек-Алмейра, К. Андлера и других, посвященные модели расчета оптимальной партии заказа и ее модификаций, например модели размера производственного заказа. Сегодня считается, что формула для расчета оптимального размера заказа (ЕОО,) составляет "золотой фонд" современной логистики, однако вопрос авторства этой модели остается предметом дискуссий.
Научная дискуссия
Согласно американским источникам, в период с 1915 по 1922 г., несколько авторов (R. Davis, Н. Owen, R. Wilson, W. Miller, G. Pennington, H. McGill, F. Clark, G. Mellen), действуя независимо друг от друга, получили формулу для наиболее экономичного размера партии, минимизирующего общие издержки хранения товара для случая, когда сирое известен и является постоянной величиной. Существует мнение, что время появления модели оптимального размера заказа (партии поставки) и вывод формулы EOQ, получившей название "формулы Уилсона", датируется в пределах от 1916 до 1934 г., когда была опубликована статья Р. Уилсона.

Рис. 3.5. Укрупненная структуризация моделей и методов научной базы логистики[1]
Считается, что в 1913 г. Форд Харрис также вывел формулу экономичного размера партии при планировании запасов незавершенного производства. Согласно проведенным исследованиям (Operation Research Society of America, 1990 г.) зависимость общих затрат в работе Ф. Харриса была записана так:

где М — ежемесячное потребление продукции, ед.; С — стоимость единицы продукции; X — искомая партия заказа, ед.; 5 — затраты, связанные с организацией заказа.
Величина 240, входящая в формулу (3.1), включает в себя 2-12//, где г — доля от стоимости продукции, приходящаяся на затраты по храпению; при этом принято, что / = 0,1. После несложных преобразований, аналог которым вы найдете при изучении гл. 6, получим:

Следовательно, Форд Харрис сформулировал модель для расчета оптимального размера заказа раньше, чем это сделал Р. Уилсон, и при оценке затрат на хранение учитывал среднюю величину заказа. Справедливости ради следует подчеркнуть, что в своей статье он не приводит формулу для X , а только описывает ее словами, а именно: "Значение А', при котором У принимает минимальное значение, определяется как корень квадратный из выражения (240М5, деленного на С)"[2] (перевод наш. — Прим. авт.).
Однако А. П. Долгов[3] приводит совсем другую трактовку вывода формулы (3.2), согласно которой Ф. Харрис получил аналитическую зависимость для расчета экономичного размера партии незавершенного производства в 1913 г. в следующем виде:

где Р — затраты на подготовку обработки партии деталей (изделий); .9 — дневной темп (интенсивность) выпуска; С — себестоимость единицы продукции; К — постоянная величина, в которую входят такие слагаемые, как процент на капитал, складские расходы, страховые взносы, налоги и пр.
Профессор А. П. Долгов полагает, что формула производственного запаса достаточно близка по своему виду к выражению (3.2), но все же имеет некоторые различия. Попытаемся в них разобраться. Запишем формулу (3.2) в виде

После интегрирования получим:

или, возвращаясь к общим затратам, —

Нетрудно заметить, что, во-первых, зависимость (3.1) включает в себя четыре параметра (С, X, 5, /), а зависимость (3.4) — пять (Р, 5, С, О, К); во-вторых, средняя величина запаса в формуле (3.1) равна -(2, тогда как в формуле (3.4) она принимается пропорциональной £); в-третьих, в анализируемых формулах используются различные подходы к учету составляющих затрат. Так, в формуле (3.1) Ф. Харрис, по существу, впервые ввел добавленную стоимость:
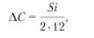
которая суммируется с затратами на хранение.
У формулы определения оптимального размера заказа есть также и другие названия, встречающиеся в различных литературных источниках: формула Ка.миа, Андлера, Боуля — Тобина (финансовый менеджмент).
Также к рассматриваемому периоду развития теории логистики относятся модели, позволяющие определить координаты склада (В. Лаупхардт, А. Вебер), методы определения групп в исследуемых выборках данных (В. Парето, Н. F. Dicky), формулировку задачи линейного программирования и алгоритмы ее решения (Л. В. Канторович, Дж. Данциг, М. Вуд) и др. В работах К. Эрроу, Т. Уайтина, Г. Вагнера, Р. Феттера, Р. Брауна и других ученых, опубликованных в 1940—1950-х гг., были рассмотрены динамические и вероятностные модели управления запасами, предложены решения многономенклатурных и многопродуктовых задач с учетом различного вида ограничений, однопериодных стохастических задач; началось систематическое изучение и были получены первые результаты по формированию моделей (стратегий) управления запасами.
В табл. 3.71 приведена эволюция моделей и методов, которые лежат в основе принятия большинства решений в области логистики. Безусловно, хронологические данные и авторство некоторых моделей и методов, приведенных в табл. 3.7, продолжают и сегодня оставаться дискуссионными и в дальнейших исследованиях будут дополнены и учтены.
Таблица 3.7. Эволюция моделей и методов теории логистики



