Доходность портфеля ценных бумаг

Предположим, что инвесторы измеряют свои доходы от ценных бумаг в виде процента от величины первоначальных затрат. Тогда ожидаемая доходность (норма прибыли) i-й ценной бумаги может быть вычислена по следующей формуле:

где 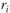– норма прибыли на i-ю бумагу, %; – прогноз будущей рыночной стоимости ценной бумаги в конце анализируемого периода с учетом дивидендов; – размер первоначальных инвестиций.

Ожидаемая доходность портфеля, как уже отмечалось, может быть рассчитана как средневзвешенная величина из индивидуальных оценок доходности входящих в портфель ценных бумаг (активов):

где 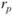– ожидаемая доходность портфеля; – доля затрат, инвестируемых в ценную бумагу г; п – число ценных бумаг (активов) в портфеле.

Проиллюстрируем расчет ожидаемой доходности инвестиционного портфеля, используя для этого данные, приведенные в табл. 3.8.

Предположим, что ожидаемая доходность ценных бумаг, входящих в портфель, составит А – 16,2; В – 24,6; С – 22,8%.

Тогда

Таблица 3.8

Портфель ценных бумаг

Ценные бумаги	Количество ценных бумаг в портфеле, шт.	Начальная рыночная цена одной ценной бумаги, ден. ед.	Сумма инвестиций, ден. ед.
А	100	40	4000
В	200	35	7000
С	100	62	6200
Начальная стоимость портфеля, ден. ед.			17200

Из приведенного расчета следует, что инвестор, поставивший перед собой цель – максимизацию доходности, – должен, казалось бы, включить в свой портфель только один вид актива, характеризующийся наивысшей эффективностью (в нашем примере – ценные бумаги В). Однако такой экстремальный подход, совершенно игнорирующий аргумент (показатель) риска, вряд ли можно считать практически приемлемым, так как в реальной действительности наблюдается закономерность роста степени рискованности ценных бумаг с возрастанием их доходности (т.е. имеет место прямая зависимость между этими двумя характеристиками ценных бумаг). Поэтому большинство инвесторов стремятся диверсифицировать свой портфель (не складывать яйца в одну корзину), снижая тем самым риск от потери своих средств при осуществлении портфельных инвестиций.

Риск инвестиционного портфеля

Общепринятой для инвесторов мерой риска, связанной с каждой ценной бумагой, служит разброс (вариация) доходов по ценным бумагам относительно ожидаемых но ним уровням доходов. В качестве показателя вариации – степени риска портфельных инвестиций наиболее часто используется показатель среднеквадратического отклонения^[1] (дисперсии). В то время как ожидаемая доходность портфеля представляет собой взвешенную среднюю доходностей отдельных ценных бумаг, его составляющих, неопределенность, связанная с любым портфелем, состоящим из нескольких ценных бумаг, нс может быть измерена простым средневзвешенным значением их отдельных среднеквадратических отклонений (или дисперсий).

Этот результат был бы правильным, если бы цены на акции и, соответственно, их доходности изменялись в совершенно одинаковом направлении – при росте одной акции точно так же вела бы себя и другая акция. В действительности, как правило, дело обстоит иначе, поэтому риск портфеля не является взвешенной средней среднеквадратических отклонений индивидуальных акций в портфеле.

Неопределенность портфеля зависит от степени, в которой доходы по каждой паре ценных бумаг изменяются совместно. Портфели, состоящие из цепных бумаг, на которые оказывают влияние одни и те же факторы, более рискованные, чем те комбинации ценных бумаг, в которых на различные ценные бумаги оказывают влияние различные факторы. Расчет среднеквадратического отклонения портфеля как простого средневзвешенного из среднеквадратических отклонений но всем ценным бумагам, входящим в портфель, означал бы игнорирование этой взаимосвязи, или ковариации, доходностей ценных бумаг, кстати, не оказывающей влияния на величину ожидаемой доходности портфеля.

В общем случае коэффициент ковариации характеризует зависимость двух случайных величин х и у и рассчитывается по формуле , т.е. как среднее арифметическое из произведений отклонений случайных величин х и у от своих средних х и . Для рассматриваемого примера положительное значение ковариации показывает, что доходности двух ценных бумаг имеют однонаправленную тенденцию изменения.

Отрицательный коэффициент ковариации означает, что анализируемые доходности имеют тенденцию компенсировать друг друга. Например, лучшая, чем ожидалась, доходность одной ценной бумаги сопровождается, как правило, худшей, чем ожидалась, доходностью другой. Нулевое (или близкое к нулевому) значение коэффициента ковариации означает отсутствие или очень слабую взаимозависимость между доходностями соответствующих ценных бумаг.

Понимание сути расчета среднеквадратического отклонения доходности портфеля приводит к удивительному выводу. Рискованность портфеля зависит не столько от рискованности отдельных ценных бумаг, сколько от ковариации попарных их комбинаций. Это значит, что сочетание рискованных по отдельности ценных бумаг может представлять собой портфель со средним и даже малым риском, если динамика доходности ценных бумаг не "связана жестко" между собой. В целом низкая ковариация обеспечивает низкий уровень риска всего портфеля.

Среднеквадратическое отклонение доходностей для инвестиционного портфеля в целом σΡ рассчитывается как взвешенная сумма ковариаций всех пар акций в портфеле, где каждая ковариация взвешена на произведение весов каждой пары соответствующих акций, а ковариация акции с самой собой представляет дисперсию данной акции. В общем случае вычисление стандартного отклонения портфеля, состоящего из п ценных бумаг, требует двойного суммирования п ценных бумаг, для чего необходимо сложить п2 членов:

где n – общее количество различных ценных бумаг в портфеле; , 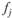– доля средств инвестированная соответственно в ценные бумаги i и j; – ковариация доходностей ценных бумаг i и j.

Таким образом, общий риск портфеля зависит:

1) от относительной доли каждой ценной бумаги в инвестиционном портфеле;

2) величины их относительных дисперсий или среднеквадратических отклонений;

3) тесноты связи между уровнями их доходностей.

Основоположником рассматриваемой "портфельной теории" является лауреат Нобелевской премии по экономике (1990 г.) Гарри Марковиц

^[2]. В центре внимания стратегии диверсификации Г. Марковица находится, как это следует из всего вышесказанного, уровень ковариации доходностей активов портфеля. Ключевой вклад Марковица состоит в постановке вопроса о риске активов как составляющих единого портфеля, а не отдельно взятых единиц. Данная стратегия, стремясь к максимально возможному снижению риска при сохранении требуемого уровня доходности, состоит в выборе таких активов, доходности которых имели возможно меньшую положительную корреляцию. Именно учет взаимной корреляции доходностей активов с целью снижения уровня портфельного риска отличает стратегию диверсификации Г. Марковица от стратегии обычной (наивной) диверсификации.

Алгоритм диверсификации портфеля активов с учетом корреляции доходностей составляющих его ценных бумаг рассмотрим на примере оптимизации структуры портфеля, содержащего в стартовом варианте три акции А, В, С с соответствующими удельными весами в общей стоимости портфеля:

Доходность рассматриваемых ценных бумаг представлена в табл. 3.9.

Таблица 3.9

Доходность акций

Акция	Доходность, %, в моменты времени
	t = 1	t = 2	t = 3	t = 4	t= 5
А	9,6	10,1	11,4	11,7	12,2
В	14,2	15,9	15,3	14,1	15,5
С	7,9	8,2	6,8	8,7	8,4
п	12,8	11,3	11,9	12,4	11,6

Для нахождения связи между доходностями каждой акции рассчитаем ковариацию (корреляцию) каждой пары акции по формуле^[3]

и ковариацию акции с самой собой

Примечание. При вычислении средних арифметических величин из и значений переменных предполагается, что все п значений – независимые. В этом случае их средние арифметические величины находятся делением суммы п значений соответствующих переменных на число п. При вычислении же ковариации используются, как известно, значения средних величин, которые в свою очередь зависят от исходных значений соответствующих переменных. В этом случае одна степень свободы теряется и средняя арифметическая из произведений отклонений случайных величин x и у от своих средних 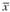и 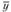находится делением 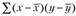на (п – 1), а не на п.

При проведении практических расчетов соответствующие коэффициенты ковариации целесообразно записывать в виде так называемой ковариационной матрицы, которая для рассматриваемого нами примера имеет следующий вид (на главной диагонали матрицы располагаются дисперсии доходности ценных бумаг):

Располагая теперь необходимой информацией, рассчитаем степень риска для рассматриваемого инвестиционного портфеля:

Сформируем теперь новый портфель, заменив акцию А па акцию D, оставив ее долю прежней, т.е. .

Используя данные, представленные в табл. 3.9, рассчитаем соответствующую изменившимся условиям новую матрицу ковариации доходностей:

Риск таким образом диверсифицированного портфеля 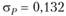(13,2%), т.е. в пять раз ниже предыдущего. Это объясняется снижением (по сравнению с акцией А) корреляции доходностей акций D и С, а также наличием отрицательной ковариации по доходностям активов D и В. Кстати, доходность второго портфеля даже несколько повысилась, так как средний уровень доходности по акциям D равен 12%, а по акциям А – 11%.

Анализ значений риска рассмотренных портфелей показывает, что риск портфеля может быть более низким, чем риски отдельных ценных бумаг, входящих в портфель; комбинация активов со слабой корреляцией понижает риск портфеля в целом, а эффективная диверсификация достигается не просто добавлением активов к портфелю, а добавлением таких активов, доходы которых имеют самые низкие уровни корреляции (а лучше и отрицательные) с активами, присутствующими в портфеле. К сожалению, активов с малой и отрицательной корреляцией существует совсем немного. В этих условиях даже успешная комбинация акций в портфеле снижает риск, но не исключает его полностью.

Поскольку на фондовом рынке обращаются ценные бумаги сотен и даже тысяч различных эмитентов, существует множество вариантов комплектования портфеля. Очевидно, что в принципе можно сформировать несколько портфелей, имеющих, например, одинаковую ожидаемую доходность, но при этом характеризующихся различным уровнем риска.

Поэтому в теории портфеля разработаны методы формирования эффективных, по определению Г. Марковица, портфелей (рис. 3.18).

Эффективный портфель – портфель, обеспечивающий минимальный риск при заданном уровне доходности (r*) или, наоборот, – наибольшую доходность при заданном уровне риска (σ)).

Рис. 3.18. Основные модели диверсификации портфеля активов

В результате решения представленных на рис. 3.18 моделей может быть сформировано множество эффективных портфелей. Важно при этом понять, что не существует единственного эффективного портфеля, который был бы эффективнее всех остальных. Средствами линейного программирования метод Марковица предлагает "меню" эффективных портфелей. Как у всякого меню, у него две стороны: с одной стороны, желания инвестора, с другой – цена. Чем выше ожидаемый доход, тем больше риск. Но каждый из эффективных портфелей этого меню обеспечивает максимальный ожидаемый доход для заданного уровня риска или минимальный уровень риска для заданного ожидаемого дохода инвестора.

Формализуя принцип определения множества эффективных портфелей, будем считать конкретный портфель эффективным, если никакой другой портфель не обещает:

1) такого же дохода при меньшем уровне риска;

2) более высокого дохода при таком же уровне риска.

Выполнение этих двух правил, называемых принципом доминирования, позволяет выделить так называемую границу эффективности ЕЕ (рис. 3.19). Все точки, расположенные на кривой EF и ниже, представляют возможные комбинации дохода и риска, все точки выше кривой EF соответствуют неосуществимым комбинациям. В частности, точка В дает комбинацию риск – доход, которую не может обеспечить ни одна из существующих инвестиционных возможностей.

Рис. 3.19. Граница эффективности в портфельном анализе

Границу эффективности определяют как набор портфелей, обеспечивающих максимальный доход для каждого заданного уровня риска или минимум риска для каждого заданного уровня дохода. Предположим, что компания установила для себя предельную величину риска σD. Выбрав портфель D, она может получить доход rD или передвинуться в попадающую на границу эффективности точку С и получить больший по величине доход rC при том же уровне риска. Следовательно, портфель С доминирует над портфелем D, ему и отдают предпочтение.

Сходные рассуждения возможны и в терминах риска. Если компания хочет получить доход rD, она выберет портфель А, поскольку он предполагает получение такого же дохода, как в случае выбора портфеля D, однако при меньшем уровне риска (σA < σD).

Инвестор, принимающий решения, будет, естественно, выбирать портфели, соответствующие точкам, лежащим на кривой границы эффективности (на траектории эффективных портфелей). Изгиб кривой границы эффективности зависит от корреляции между активами. При коэффициенте корреляции +1, кривая эффективности вырождается в прямую линию (практически невозможный вариант). Чем ниже коэффициент корреляции, тем больше кривизна границы эффективности.

Далее инвесторам предоставляется возможность выбрать в соответствии со своими предпочтениями портфель, оптимальный в рамках выбранной ими агрессивной или оборонной стратегии. В частности, так называемые "консервативные" инвесторы (т.е. те, кто заинтересован в сохранении своих капиталов и получении постоянной и предсказуемой прибыли) будут отдавать предпочтение портфелям, лежащим в более левой нижней части кривой эффективной границы Марковица. Более "агрессивные" инвесторы (те, кто идет на более высокий риск в надежде получить более высокую, по менее определенную ожидаемую отдачу) будут формировать свои портфели, находящиеся в верхней правой части кривой эффективности Марковица.

В духе фон Неймана и Моргенштерна теория Марковица предлагает метод максимизации выгоды (полезности) для каждого конкретного инвестора. Это единственный момент, в котором теория Марковица имеет дело с субъективными устремлениями инвесторов. Все остальное в ней строго математизировано.