Динамическое прогнозирование

Для формирования методологии прогнозирования инвестиционной деятельности в экономических системах рассмотрим пример прогнозных оценок для линейной модели регрессии вида:

где – расчетное значение результирующего показателя у в точке i; – фактическое значение воздействующего фактора в точке i; – параметры модели, получаемые в результате статистической обработки фактических значений пар данных

Точечный прогноз в при этом определяется выражением

То есть, опираясь на данные статистической выборки и построив однофакторную линейную регрессионную модель на основе значений воздействующего фактора , можно, задавшись значением воздействующего фактора, лежащего за пределами диапазона , найти значения результирующего показателя у, подразумевая, что тенденция зависимости у от х за пределами диапазона полученных наблюдений не изменится. Тогда, в случае точного прогноза, значение результирующего показателя у, соответствующее значению воздействующего фактора будет лежать на линии регрессии.

Однако, поскольку значения фактических наблюдений, как правило, не лежат на линии регрессии, то и точечный прогноз нс является достоверным. Поэтому используется интервальный прогноз, подразумевающий, что истинное значение результирующего фактора у, соответствующего , находится в определенном диапазоне (интервале), величина которого зависит от степени доверия, с которым стремятся получить результат, и увеличивается по мере удаления от диапазона фактических наблюдений :

где – ошибка прогноза; – коэффициент Стьюдента, вносящий поправку в ошибку прогноза с учетом объема исходных наблюдений п и требуемым уровнем доверительной вероятности β.

Ошибка прогноза имеет две причины.

• Первая причина связана с выбором вида модели

регрессии. Любая совокупность фактических данных может быть описана различными типами регрессионных моделей. Помимо линейной модели те же данные могут быть описаны моделями типа:

– параболическая;

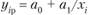– гиперболическая;

– показательная;

– степенная

и др.

Вне зависимости от вида модели в конечном счете ее качество будет определяться так называемой остаточной дисперсией:

• Вторая причина связана с оценкой точности параметров модели регрессии.

В рассматриваемом случае – это ошибки определения статистических коэффициентов .

Поскольку первая причина связана с выбором модели регрессии (так называемая немодельная ошибка – ), а вторая связана с точностью нахождения параметров модели регрессии (так называемая модельная ошибка – ) и не зависит от выбора вида модели, то согласно правилу дисперсий дисперсия ошибки прогноза как дисперсия суммы двух независимых величин определяется как сумма дисперсий этих величин: .

Ошибка в определении а0 при условии, что на результат у не влияют другие факторы помимо х, связана с недостаточностью объема наблюдений. Здесь можно провести аналогию со стандартной ошибкой из математической статистики.

Таким образом, стандартную ошибку можно интерпретировать как недостаточность объема наблюдений, что приводит к смещению линии регрессии относительно начала координат при условии, что величина воздействующего фактора .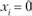

Ошибка определения статистического коэффициента вычисляется по формуле

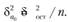
Ошибка определения статистического коэффициента связана с тем, что коэффициент в отличии от коэффициента , не зависящего от фактора х, наоборот, характеризует силу связи фактора х с результатом у. Чем больше значение коэффициента , тем мощнее рычаг воздействия на результат у изменения на одну единицу фактора х (рис. 9.10).

Рис. 9.10. Ошибка определения статистического коэффициента a1

Если ошибка определения статистического коэффициента не зависит от глубины прогноза, то ошибка определения статистического коэффициента , характеризующего угол наклоналинии регрессии относительно оси абсцисс, пропорциональна глубине прогнозируемой оценки. В то же время ошибка определения статистического коэффициента будет тем меньше, чем шире база значений аргумента от до :

Поскольку параметр не связан с воздействием х, а параметр связывает воздействие х и результат у, то эти параметры, а значит и ошибки их определения, можно считать независимыми и, согласно правилу дисперсий, модельную ошибку прогноза можно записать:

Взаимосвязь трех ошибок в определении прогнозных ошибок по регрессионной модели имеет вид

Таким образом, все составляющие ошибки прогнозируются независимыми величинами и дисперсия прогноза как сумма независимых величин будет равна сумме их дисперсий .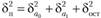

Прогнозная оценка в ее интервальном варианте бывает средней и индивидуальной:

Вне зависимости от числа параметров модели регрессии все параметры, связанные с воздействующими факторами, будут формировать ошибки, зависящие от глубины прогноза.

Как при средней, так и при индивидуальной прогнозной оценке наибольший вклад в ошибку прогноза вносит большое удаление точки прогноза (xп) от середины исследуемого интервала значения х.

Без сомнений, в условиях множества неопределенностей внутреннего и внешнего характера для предприятия при создании методологии прогнозирования инвестиционной деятельности в экономических системах, реализующих ИТ, необходимо использовать интервальные прогнозные оценки. При этом независимо от того, будет ли это интервальный индивидуальный или интервальный средний прогноз, очевидно, что незначительной может быть ошибка прогноза инвестиционной деятельности организации только в рамках одного цикла развития.

Теория коротких циклов продолжительностью 3–3 с половиной года, которые характеризуют динамику развития той или иной отрасли, вполне может быть использована для прогноза инвестиционной деятельности организации. Но эта теория коротких циклов при описывании прогноза инвестиционной деятельности в экономических системах, реализующих ИТ, должна быть использована в сочетании со средними (торгово-промышленными) циклами продолжительностью 7–11 лет, которые характеризуют волнообразное развитие экономики в масштабах государства, и большими циклами продолжительностью 48–55 лет, которые характеризуют волнообразные тенденции развития мировой экономики.

В рамках развития методологии анализа, методов оценки, моделирования и прогнозирования инвестиционной деятельности в экономических системах разработана методология исследования многофакторной модели "инновация – рынок", представленная на рис. 9.11, для определения характеристик эффективности инвестиций в информационные технологии в пределах организации^[1].

Эта модель содержит:

– полностью регулируемые факторы (инновации в ИТ, снабжение ресурсами ИТ, производство ИТ, сбыт продукции ИТ и управление процессом реализации ИТ);

Рис. 9.11. Многофакторная модель "инновация – рынок" для определения характеристик эффективности инвестиций в ИТ в пределах организации

– частично регулируемые факторы (взаимоотношения организации с инвесторами, конкретными потребителями ИТ, поставщиками ресурсов и рынком, в том числе конкурентами);

– неуправляемые факторы (экономика и политика, законодательство и право, социальная и культурная среда, географические, климатические и экологические условия).