Диалектическая сущность информации

Анализируя понятие "информация" с учетом вводимых мер, А. А. Денисов показывает, что информация не удовлетворяет логическому закону исключенного третьего, не допускающему существование нескольких противоречивых, но одинаково истинных величин, суждений, и делает вывод, что информация – это понятие, не поддающееся анализу средствами формальной логики и требующее применения к нему диалектической логики, которая обеспечивает возможность анализа не только абсолютно, но и относительно истинных высказываний [1, с. 243].

По Денисову, материя выступает как диалектический синтез субстанции и отражения (информации), где информация – это структура материи. Так что материя, с одной стороны, субстанция (вещество), но, с другой стороны, содержит информацию ^[1].

Все это относится и к информации, которая циркулирует как между материальными объектами в процессе их взаимодействия, так и внутри континуума, реализуя материальное единство мира. Эта информация, с одной стороны, вполне объективно реальна, поскольку не зависит от нашей воли, но, с другой стороны, даже внутри материального континуума распространение информации сопровождается помехами и искажениями, так что ее получатели реально имеют дело не с информацией "в себе", а с информациями "для них", подобными информации "для нас", которые все-таки тоже объективно реальны в той же мере, как и сама материя. При этом ни информация не может существовать без материального носителя, ни материя не может быть бесструктурной, т.е. бессодержательной.

Таким образом, основной вопрос философии о первичности материи или сознания (информации) теряет смысл и становится атрибутом истории философии, ибо нет и никогда не было материи без информации, как нет информации без материи.

Как было отмечено выше, информация измеряется не числом в понимании классической логики. Классическая логика – это логика чисел, а диалектика – логика слов и выражаемых ими понятий.

Конструируя сущность понятия Н, А. А. Денисов вначале пользовался аналогиями теории цепей, а затем сделал доклад на семинаре В. С. Тюхтина в Институте философии АН СССР, и Виктор Степанович увидел в модели А. А. Денисова возможность вывода его символических представлений из последовательности требований, предъявляемых законами диалектики применительно к суждению.

В результате получилась модель, отображающая процесс отражения, восприятия и осмысления информации с учетом времени реакции и ригидности (сопротивляемости новой информации) воспринимающего субъекта ^[2].

В процессе конструирования сущности понятия Н в его символическом представлении последовательно учитываются требования, предъявляемые законами диалектики применительно к суждению.

Первым для введения меры логической информации был применен так называемый "основной закон логики", справедливый как для классической логики, так и для диалектики. Согласно этому закону сущность Я понятия обратна его объему п (1.15).

Здесь под объемом понятия подразумевается общее число однородных объектов или явлений, информация J о которых легла в основу понятия. При этом, чем больше объектов, тем меньше в расчете на один из них следов информаций Jk, присущих только одному или немногим объектам. И в результате при п → ∞ от них ничего не остается (как это случилось с понятием материи).

Напротив, при п = 0, т.е. в случае идеального (несуществующего) объекта, сущность информации о нем бесконечна, однако она ни о чем. Поэтому философия, понятия которой охватывают все сущее, вправе судить обо всем, однако такие суждения с неизбежностью безадресны, неконкретны.

Напротив, математика идеальных чисел абсолютно конкретна в своих заключениях, которые при этом, строго говоря, не имеют отношения к реальным объектам.

Зато, при п = 1, т.е. применительно к единственному объекту, понятие совпадает с полной информацией J о нем, сохраняя все индивидуальное богатство красок и оттенков. Поэтому, например, понятие о конкретном Иванове неизмеримо богаче понятия о мужчине и тем более о человеке вообще, ибо мы можем точно указать его рост, вес, цвет глаз и даже число шрамов на теле, в то время, как о человеке вообще можно сказать гораздо меньше, да и то в среднем.

Второй закон в числе законов, формирующих логическую информацию – закон развития, или закон изменчивости ("Все течет и все изменяется"). Это сугубо диалектический закон, поскольку в классической логике А всегда есть A и 1 есть 1, в то время как в диалектике становление истины идет непрерывно и никогда не заканчивается, во-первых, потому, что изменяется реальность, а во-вторых, совершенствуется само знание, так что никто не может претендовать на знание истины в последней инстанции.

Как показано выше, информация отражает относительную истину и может изменяться в процессе познания и практики. Чтобы описать процесс становления понятия введен символ (оператор) d/dt, где числитель означает частичное изменение, а знаменатель указывает, что это изменение происходит во времени, так что, например, dJ/dt означает изменение информации во времени. При этом накопление или убывание информации можно отразить знаками "+" и "-" соответственно.

Поскольку всякое изменение отрицает стабильность, т.е. ранее неизменное, то закон изменчивости с равным основанием мог бы быть назван законом отрицания; причем символ d/dt есть синоним частичного отрицания и соответствует словесному "в какой-то мере не".

С учетом рассматриваемого закона сущность Hτ процесса изменения (эволюции) понятия должна быть обратно пропорциональна уже не объему понятия п, а изменению этого объема понятия dn/dt = 1/τ, так что

Hz = τdJ/dt. (1.19)

В дальнейшем т именуется информационным сопротивлением и характеризует задержку при восприятии новой информации в процессе становления и эволюции понятия.

Третий закон диалектики – закон отрицания отрицания – без формализации наиболее труден для понимания.

Так J есть тезис, Δ1J есть антитезис, т.е. отрицание J, а Δ2J есть анти-антитезис, отрицание отрицания J. Другими словами, если J есть А, то Δ1J есть "неА", a Δ2J есть "ненеА", т.е. определенный, хотя и неполный в отличие от классической логики возврат к А.

Это и есть знаменитое развитие по спирали, чреватое циклическими возвратами к изначальным формам, но с иным уже ОГЛАВЛЕНИЕм.

Поскольку закон изменчивости является по своей сути законом отрицания, то закон отрицания отрицания следует трактовать как двукратное применение закона изменчивости, т.е. как применение закона изменчивости к самому закону изменчивости. С формально-символической точки зрения это означает применение оператора d/dt к самому оператору d/d(, т.е. d(d/dt)/dt или d2/dt2, так что, например, d2J/dt2 означает изменение эволюции информации во времени.

Сущность HL изменения эволюции понятия должна быть в этом случае обратно пропорциональна изменению эволюции объема понятия d2/dt2 = = 1 /L, так что

(1.20)

где L будем именовать ригидностью (негибкостью) понятия, сопротивляемостью изменению.

Закон отрицания мог бы быть применен еще раз, т.е. к закону отрицания отрицания, что привело бы к закону отрицания отрицания отрицания, символически отображаемому d3J/dt3. Можно было бы говорить и о дальнейшем применении закона отрицания. Однако, по-видимому, диалектика не напрасно не содержит законов тройного и более отрицаний, поскольку это было бы слишком громоздко и обременительно для мышления. Наше мышление действует экономно, и все явления, выходящие за рамки закона отрицания, разбивает на транзитивные формы и т.д., которые в совокупности передают сколь угодно сложные процессы.

Четвертый закон диалектики, требования которого нужно учесть, – закон единства противоположностей – требует избегать абсолютизации как момента борьбы, так и момента солидарности противоположностей, которые и возникают-то вследствие субъективного расчленения единого целого ради облегчения познания противоречивых частей его.

Противоположностями в нашем случае являются момент относительной стабильности понятия, соотношение (1.15) – тезис, момент относительной изменчивости (1.19) – антитезис, опосредованные отрицанием отрицания (1.20), которые в соответствии с применяемым законом следует рассматривать в неразрывном единстве

(1.21)

а в частном случае возможна линейная аппроксимация

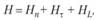(1.21, а)

где п – объем понятия; τ – информационное сопротивление, характеризующее задержку при восприятии новой информации в процессе становления и эволюции понятия; L – ригидность (негибкость) понятия, сопротивляемость изменению.

Таким образом, в результате получается соотношение

(1.22)

Это значит, что истинная суть H объективной реальности слагается в каждый момент времени из сформировавшегося к этому моменту содержимого памяти Нп (отраженной сути), из той логической информации Нτ, которая пребывает в процессе передачи органов чувств к памяти, и из той логической информации HL, усвоению которой препятствуют привычки и предрассудки.

Пятый диалектический закон – всеобщей взаимосвязи и взаимозависимости явлений требует учета всех факторов, определяющих исследуемый процесс, а не только тех, что кажутся доминирующими.

С учетом закона всеобщей взаимосвязи и взаимозависимости явлений соотношение (1.15) дополняется составляющими, отражающими взаимодействие исходного понятия с другими понятиями, входящими в систему, путем введения соответствующих обозначений для того, чтобы отличить эти составляющие друг от друга. Тогда

(1.23)

где Hni – системная суть понятия; первый индекс при символах означает номер понятия, учитываемого при отображении системы, а второй – номер понятия, с которым взаимодействует данное, так что пii означает собственный объем i-го понятия; nij – взаимный объем i-го и j-го понятий.

Полученное соотношение (1.23) соответствует обычному правилу формальной логики, согласно которому в любом определении Hn1 должны присутствовать, во-первых, его родовая принадлежность J1 а, во-вторых, видовые отличия J2, J3 и т.д.

Аналогично соотношение (1.19) преобразуется к виду

(1.24)

где Hτi – системная суть эволюции i-го понятия; τii – собственное информационное сопротивление; τij – взаимное информационное сопротивление i-го и j-го понятий.

А соотношение (1.20) принимает форму, аналогичную соотношениям (1.23) и (1.24), т.е.

(1.25)

где НLi – системная суть изменения эволюции понятия; Lii – собственная ригидность данного понятия; Lij – взаимная ригидность i-го и j-го понятий.

В результате с учетом закона всеобщей взаимосвязи и взаимозависимости получим систему соотношений:

(1.26)

или в случае линейной аппроксимации и некоторых перестановок составляющих, что удобнее для ряда приложений, получим:

(1.27)

Система размытых относительно истинных (диалектических) суждений типа (1.27) позволяет сделать символическое размытое умозаключение путем решения этой системы по правилам, отличающимся от математических в той мере, в какой диалектическая логика отличается от классической, т.е. в меру влияния законов тождества и исключенного третьего. Отсутствие этих законов в классической логике, фактическая замена их законом единства противоположностей, приводит к тому, что с одной стороны, в отличие от математики суждения типа (1.27) всегда совместны, ибо размывая область их существования, всегда можно их частично совместить, а с другой стороны, линейные комбинации этих суждений не являются тавтологиями, ибо в силу размытости не вполне сводятся друг к другу.

В частных случаях (что определяется на этане обоснования модели конкретной проблемной ситуации) соотношение (1.22) может рассматриваться как обычное дифференциальное уравнение, а система уравнений (1.27) может решаться в соответствии с принятой в математике процедурой преобразования и решения дифференциальных уравнений, учитывающей логический закон достаточного основания (в соответствии с которым число суждений должно быть не меньше числа объектов, о которых должно быть получено умозаключение), логические законы противоречия (требующий непротиворечивости, совместимости суждений) и тождества (требующий изображать синонимы одним и тем же символом).

Шестой закон диалектики – закон перехода количественных изменений в коренные качественные – акцентирует внимание па необходимости избегать абсолютизации тенденций развития, выявленных в начале процесса, ибо в дальнейшем они могут измениться вплоть до своей противоположности, причем именно вследствие развития.

Из этого закона следует также, что сумма свойств частей не есть свойство целого, а отрицание целого не обязательно означает отрицание частей, ибо может относиться к отрицанию лишь того нового свойства, которое возникло вследствие синтеза частей.

Этот закон требует понимания того, что характеристические константы п, т и L являются константами лишь в ограниченном диапазоне эволюционных изменений понятия. В общем же случае, при больших изменениях, эти константы могут не сохранять своих значений, что приведет к радикальному (революционному) изменению сути понятия, нарушив плавный эволюционный ход развития. С формальной точки зрения это означает, что в общем случае п, τ и L являются функциями H,_J, dJ/dt, d2J/dt2.

Отметим, что хотя параметры n, τ и L названы выше соответственно емкостью (объемом памяти), информационным сопротивлением и ригидностью понятия, но поскольку последнее формируется в сознании одного человека (или в перспективе – в памяти конкретной системы восприятия и хранения информации с использованием ЭВМ), то эти параметры, по существу, характеризуют память, пропускную способность и ригидность психики конкретного человека (или автоматизированной информационной системы) и могут быть измерены экспериментально, что следует периодически повторять с учетом последнего из рассмотренных законов.

Если периодически уточнять п, τ и L, то выражение (1.27) будет сохранять неограниченную универсальность при описании любых явлений; причем, описывая сложное явление поэлементно, оно сохраняет целостность, присущую соотношению (1.26).

С более подробным изложением применения законов диалектики для получения моделей информационных процессов с учетом их кинематики и динамики можно ознакомиться в [8] и работах А. А. Денисова [1, 19, 22].

Законы классической логики и диалектики различаются тем, что в первом случае любые деформации исходных суждений могут быть только скачкообразными (либо истина, либо ложь), а во втором случае все переходы плавные и непрерывные с бесконечным множеством состояний между истиной и ложью. Поэтому классическая логика бинарна, двузначна, а диалектика бесконечнозначна.

При этом следует иметь в виду, что отмеченные отличия диалектической логики от классической являются глубоко принципиальными и приводят к неоднозначности, множественности умозаключений на основе одной и той же системы суждений.

Это позволяет, в частности, поставить вопрос о выборе среди них наилучшего управленческого или проектного решения, т.е. сформулировать задачу оптимизации, которая в этой постановке сводится к поиску такого решения системы соотношений типа (1.27), в котором выбранная в качестве критерия оптимальности некая комбинация из ΔАi была бы минимальной. Это означает, по существу, поиск наименее размытого решения системы из всех возможных.

Рассмотренные законы диалектической логики и их применение для объяснения процесса становления понятия логической информации в настоящее время еще недостаточно используются. В то же время их учет представляется перспективным для развития теории информационных процессов и систем.