Временны́е модели процессов управления развитием экономики
Поскольку рассматриваемые уровни рынков (мировой – БЦЭЛ, государственный – СЦЭЛ и отраслевой – МЦЭА) носят в своем развитии цикличный характер, то их можно описать периодическим временны́м рядом, задаваемым пятью параметрами: периодом (Р) или частотой (f), амплитудой (I), фазой (
), начальным уровнем (
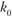) и темпом роста k1. Динамический периодический временной ряд можно представить в гармоническом виде:
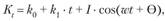(9.1)
где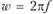 
– круговаячастота, измеряемая в радианах в единицу времени; 
; 
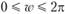– фаза.
В табл. 9.6 приведен пример обобщенных в результате исследований значений периодов (Р) и набега фаз (
) различных информационных технологий.
Выражение (9.1) часто записывается через синусы и косинусы без упоминания о фазе:
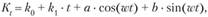
где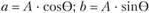 
.
Но именно набег фаз (в том числе как случайных составляющих) формирует смещения пиков рыночных подъемов и спадов, нередко воспринимаемых как "неожиданный кризис" либо как "нежданная благоприятная среда".
Тригонометрическое тождество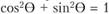 
приводит к тому, что 
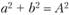. Поэтому существует взаимосвязь между амплитудой колебаний доходов и параметрами гармоники.
Таблица 9.6
Обобщенные значения периодов и набегов фаз различных информационных технологий
|
Информационная технология |
Период, лет |
Набег фазы, мес. |
|
Информационные потоки |
→0 |
→0 |
|
Интеллектуальная собственность |
1,4,8 |
0-6 |
|
Технические средства и системы, реализующие информационные технологии |
2 |
10-12 |
|
Оборудование для производства технических средств и систем информационных технологий |
4 |
6-9 |
|
Программное обеспечение для реализации информационных технологий |
2 |
10-12 |
Учитывая, что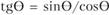 
, поделив параметр b на а, получим:
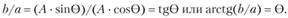
Таким образом, фаза периодического ряда изменения доходности бизнеса при формировании коротких и длинных инвестиционных циклов связана также с параметрами гармонического представления параметров а и b.
Инвестиционный цикл, как и любой динамический временной ряд, может быть представлен как сумма линейного тренда и ряда синусоид и косинусоид (рядом Фурье):
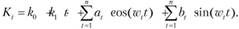(9.2)
Согласно проведенным исследованиям анализируемые ряды динамики доходности различных сегментов рынка, в том числе рынка информационных технологий, имеют конечную длину цикла. Если в диапазоне наблюдений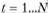 
интервалы наблюдений представляют собой постоянную величину, например месяц, то самый большой период косинусоидальной зависимостибудет равен N мес., что соответствует угловой частоте 
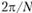. Наименьший период этой кривой составит 2 мес. (
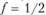), поскольку необходимо по крайней мере 2 мес., чтобы кривая завершила цикл.
Угловая частота i-й составляющей равна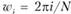
, где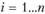 
; 
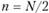. Если 
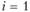, то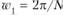 
, что соответствует самой длинной (самой медленной) из наблюдаемых волн. При 
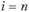имеем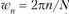 
, что соответствует самой короткой (самой быстрой) из наблюдаемых волн.
Определение параметров уравнения (9.2) может быть выполнено методом наименьших квадратов (МНК), который приводит к системе нормальных уравнений. Покажем это на примере уравнения (9.2) для случая одной гармоники:
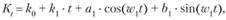(9.3)
где t принимает значения от 0 с постоянным увеличением на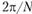 
Для нахождения параметров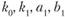 
модели (9.3) при использовании МНК необходимо решить систему дифференциальных уравнений относительно суммы квадратов ошибок по каждому из перечисленных параметров.
Расхождение фактического и расчетного значений доходности, определяемое через сумму их квадратов, образует сумму квадратов ошибок 5, вычисляемую по методу наименьших квадратов:
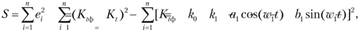
где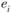
– случайная компонента как ошибка моделирования, значение которой необходимо свести к минимуму.
В результате дифференцирования суммы квадратов ошибок S
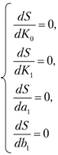
система уравнений примет вид
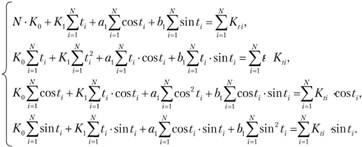
В этой системе за полные периоды N получается
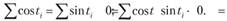
Кроме того, поскольку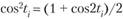
, можно показать, что
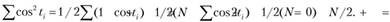
Аналогично:
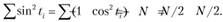
Тогда систему уравнений можно переписать в виде
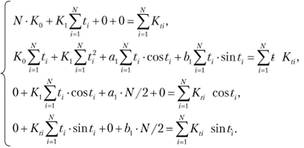
Пример моделирования доходов сегмента рынка информационных технологий с использованием 12 гармоник ряда Фурье приведен на рис. 9.9.
Рассмотрим результаты построения модели зависимости доходов, обеспечиваемых определенным сегментом рынка информационных технологий, как функции времени при использовании для описания 12 гармоник ряда Фурье (табл. 9.7). В качестве периода цикличного изменения доходности рассматривается двухгодичный интервал, соответствующий периодам обновления технических средств и систем, реализующих информационные технологии, а также программного обеспечения для реализации информационных технологий (см. табл. 9.6).
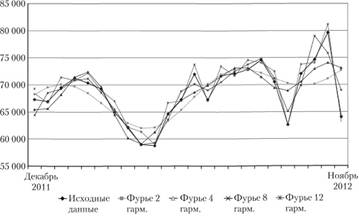
Рис. 9.9. Пример моделирования доходов по информационным технологиям с использованием ряда Фурье
Результаты моделирования показывают, что наложение на линейный тренд первой гармоники ряда Фурье приводит к удвоению коэффициента детерминации (с 0,12 до 0,24) как меры адекватности модели и тем самым подтверждает цикличный характер спроса на продукцию информационных технологий. Добавление второй гармоники ряда Фурье обеспечивает наибольшее абсолютное приращение коэффициента детерминации R2 (с 0,24 до 0,48), что демонстрирует стремление всех крупнейших компаний ежегодно предлагать своим клиентам новинки информационных технологий (см. минимальный период для интеллектуальной собственности табл. 9.6).
Следующее существенное приращение значения коэффициента детерминации связано с добавлением в модель с линейным трендом и четырьмя гармониками ряда Фурье пятой гармоники ряда (рост коэффициента детерминации с 0,65 до 0,76). Это во многом объясняется сезонным характером жизненной активности пользователей информационных технологий, в частности осенними и весенними всплесками активности в научной и учебной среде. Следующий по значимости скачок коэффициента детерминации при модельном описании доходности рынка информационных технологий связан с добавлением третьей гармоники ряда Фурье (с 0,56 до 0,65). Это во многом объясняется набегом фаз развития различных сегментов рынка информационных технологий (см. табл. 9.6). Интересно, что с добавлением к 11 гармоникам ряда Фурье 12-й гармоники значение коэффициента детерминации не возрастает. То есть за короткий промежуток времени (2 мес.) не успевают произойти существенные обновления ни в одной из комбинаций сегментов рынка информационных технологий, представленных в табл. 9.7.
Таким образом, на основе проведенных исследований можно разработать матричные модели инвестиционных вложений в информационные технологии как элемент высоких технологий, включая технические средства и системы, оборудование для их производства, программное обеспечение, информационные потоки и интеллектуальную собственность на этапах проведения научно-исследовательских, опытно-конструкторских и технологических работ; технологического переоснащения и подготовки производства; испытания, сертификации и стандартизации информационных технологий; создания и развития инновационной инфраструктуры.
Таблица 9.7
Результаты построения модели зависимости доходов, обеспечиваемых определенным сегментом рынка информационных технологий, как функции времени при использовании для описания 12 гармоник Фурье
|
Тип модели |
Характеристика модели – период изменения доходности |
Коэффициент детерминации |
|
Линейный тренд |
Поступательный линейный рост |
0,12 |
|
Линейный тренд + 1 гармоника ряда Фурье |
24 мес. |
0,24 |
|
Линейный тренд + 2 гармоники ряда Фурье |
12 мес. |
0.48 |
|
Линейный тренд + 3 гармоники ряда Фурье |
8 мес. |
0,56 |
|
Линейный тренд + 4 гармоники ряда Фурье |
6 мес. |
0,65 |
|
Линейный тренд + 5 гармоник ряда Фурье |
5 мес. |
0,76 |
|
Линейный тренд + 6 гармоник ряда Фурье |
4 мес. |
0,80 |
|
Линейный тренд + 7 гармоник ряда Фурье |
3,5 мес. |
0,85 |
|
Линейный тренд + 8 гармоник ряда Фурье |
3 мес. |
0,85 |
|
Линейный тренд + 9 гармоник ряда Фурье |
80 дней |
0,86 |
|
Линейный тренд +10 гармоник ряда Фурье |
72 дня |
0,92 |
|
Линейный тренд +11 гармоник ряда Фурье |
65 дней |
0,95 |
|
Линейный тренд + 12 гармоник ряда Фурье |
2 мес. |
0,95 |
Объединяя большие, средние и малые циклы экономической активности, выражение (9.3) можно записать в виде аддитивной суперпозиции накладывающихся периодических процессов разной амплитуды и длительности:
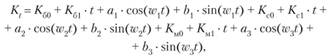(9.4)
где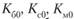 
– начальные уровни экономической активности для больших, средних и малых циклов; 
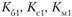– темпы линейного роста для больших, средних и малых циклов экономической активности; 
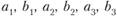– амплитуды синусоидальных и косинусоидальных составляющих колебаний соответственно для больших, средних и малых циклов экономической активности; 
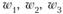– круговые частоты соответственно для больших, средних и малых циклов экономической активности.