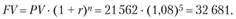Временная стоимость денег: поток платежей

Многие финансовые расчетные схемы основываются на потоках платежей, типичным примером которых служит так называемая пожизненная рента.

Бесконечный поток одинаковых платежей, осуществляемых через равные интервалы времени, представляет собой пожизненную ренту.

Например, если остаток по сберегательному счету составляет 150 тыс. долл. США и на этот счет начисляется 10% годовых с ежегодной капитализацией, то либо сам вкладчик, либо его наследники могут ежегодно получать 15 тыс. долл. на протяжении всего периода времени, пока начальная сумма 150 тыс. долл. США остается на счету.

Классическим примером бессрочного потока платежей считаются также выплаты по привилегированным акциям, когда их обладателям выплачиваются фиксированные дивиденды в течение всего времени владения данной ценной бумагой.

Предположим, для конкретности, что каждая выплата пожизненной ренты осуществляется в конце каждого текущего года. Тогда приведенную стоимость (PV) пожизненной ренты с платежами в размере С в каждом периоде при процентной ставке r можно рассчитать следующим образом:

Данное выражение представляет собой геометрическую прогрессию, сумма которой может быть определена как отношение 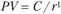^[1]

Аннуитеты

Аннуитетом называется поток одинаковых платежей, сделанных определенное количество раз через равные интервалы времени.

Предоставление потока платежей в виде аннуитета существенно упрощает количественный анализ многих коммерческих, финансовых, а также инвестиционных процессов, дает возможность использовать соответствующий набор стандартных подходов и табулированных формул. Так, при расчете приведенной стоимости аннуитета можно воспользоваться специальными таблицами, где табулированы ее значения для различных процентных ставок и количества периодов.

Для вывода аналитической формулы расчета аннуитета его можно представить как разность двух пожизненных рент: с первым платежом в период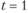и с аналогичным платежом в период 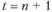(рис. 3.2).

Приведенная стоимость аннуитета может быть рассчитана в этом случае как 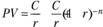, где с помощью множителястоимость второй пожизненной ренты, приведенная к моменту времени п, приводится к моменту времени .

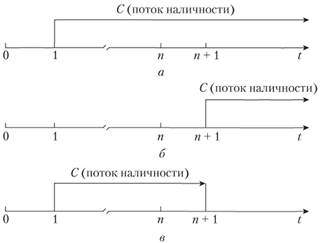
Рис. 3.2. Аннуитет как разность двух пожизненных рент:

а, б – пожизненная рента 1 и 2 соответственно; в – аннуитет

Преобразовав полученную формулу значения приведенной (текущей) стоимости аннуитета, получаем

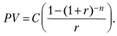
Примечание. Табулированные значения текущей стоимости аннуитета одной денежной единицы 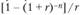приведены в приложении 2.

Пример. Предположим, вы принимаете решение о приобретении автомобиля, беря для этой цели банковский кредит, по которому можете ежемесячно выплачивать, с учетом возможностей своего бюджета, только С = 555 евро. Среди возможных вариантов получения займа вас устроил кредит на 48 месяцев иод 1% в месяц. Какую сумму вы можете (должны) занять?

Решение.

Для ответа на данный вопрос необходимо рассчитать текущую (приведенную или настоящую) стоимость 48 платежей по 555 евро каждый:

Следовательно, вы можете себе позволить взять сумму в размере 21076 евро, поскольку сможете ее выплатить.

Будущая стоимость аннуитета может быть рассчитана следующим образом:

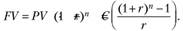
Примечание. Табулированные значения будущей стоимости аннуитета одной денежной единицы 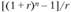приведены в приложении 2 настоящего учебника.

Пример. Инвестор планирует для обеспечения своей пенсии ежегодно откладывать по 2000 евро в течение 25 лет, получая на эти инвестиции 12% годовых. Определите, какой суммой будет располагать инвестор через 25 лет.

Решение.

Речь здесь идет о будущей стоимости аннуитета:

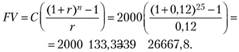
Таким образом, сразу после взноса последней суммы через 25 лет пенсионный фонд инвестора будет составлять 266667,8 евро.

В тех случаях, когда члены ренты постнумерандо изменяются по закону арифметической прогрессии (возрастающей или убывающей), наращенная сумма соответствующей ренты может быть определена по формулам^[2]:

а) в случае возрастания членов ренты:

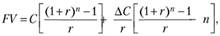
где С – первый член ренты; ΔС – величина прироста членов ренты.

б) в случае убывания членов ренты:

Пример. По условиям контракта платежи вносятся в конце года, первый платеж составляет 2,0 млн долл. США; каждый год его величина возрастает на 0,2 млн долл.; срок выплат – 4 года, ставка – 8% годовых. Определить наращенную к концу рассматриваемого периода сумму.

Решение.

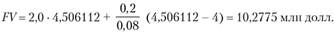
Внесем изменения в условия задачи: члены ренты не увеличиваются, а уменьшаются на 0,2 млн долл., остальные условия не меняются. В этом случае наращенная сумма равна:

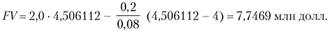
Определение размера платежа

Предположим, что вы хотите преобразовать имеющиеся на вашем счете средства 10 тыс. евро в семилетний аннуитет для того, чтобы погасить задолженность по ссуде семью равными ежегодными взносами. Если процентная ставка известна и составляет, скажем, 8% годовых, размер серийного платежа можно рассчитать по формуле

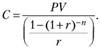
В рассматриваемом случае

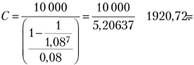
Следовательно, вы заплатите семь взносов, каждый из которых составит 1920,72 евро.

С финансовой точки зрения это выглядит следующим образом. Если положить на сберегательный счет 10 тыс. евро под 8% годовых на семилетний период и снимать по 1920,72 евро в конце каждого года, то к концу рассматриваемого срока на балансе останется нуль евро. Каждый год часть платежа представляет собой списание начисленных процентов, а оставшаяся часть уменьшает сумму оставшегося капитала.

Сначала бо́льшая часть платежа приходится на проценты, однако со временем она будет уменьшаться, так как уменьшается капитал, на который начисляются проценты. Так как выплачиваемая сумма остается постоянной (1920,72 евро), доля капитала в ней будет расти. Наконец, к концу седьмого года долг будет полностью выплачен преимущественно за счет основного капитала.

Пример. Родители студента университета Ивана Хапугина дали ему сумму, необходимую и достаточную для покупки аннуитета, состоящего из 50 ежемесячных платежей по 1000 евро, призванных покрыть мелкие текущие расходы Ивана. Однако студент решает сразу потратить 10 тыс. евро из этой суммы на приобретение подержанного автомобиля марки Volvo. Определите, какие ежемесячные платежи может обеспечить для Ивана оставшаяся сумма, если ставка процента составляет 1% в месяц?

Решение.

Рассчитаем первоначальную сумму средств, выделенных Ивану Хапугину:

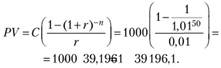
После покупки автомобиля на счете Ивана останется 29196,1 евро. Теперь можно найти, какой суммой он будет располагать ежемесячно:

Определение числа периодов (платежей) аннуитета

Воспользовавшись данными предыдущего примера, предположим, что после покупки автомобиля Иван Хапугин продолжает расходовать 1000 евро в месяц. На какой период ему хватит оставшейся после приобретения автомобиля суммы?

Для ответа на этот вопрос необходимо использовать базовую для нахождения приведенной стоимости аннуитета формулу:

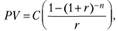
откуда

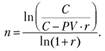
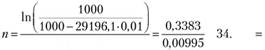
ln(1 + 0,01)

Тот же ответ можно получить с использованием таблицы "Приведенная (текущая) стоимость аннуитета" (приложение 2 табл. п. 2.1). Для этого сначала необходимо рассчитать множитель дисконтирования:

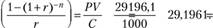
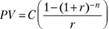
Затем в указанной таблице по известным ставке процента (1%) и множителю дисконтирования исчисляется число периодов аннуитета.

Определение размера процентной ставки. Необходимость в расчете величины процентной ставки возникает всякий раз, когда речь идет о выяснении эффективности (доходности) соответствующей финансово-банковской или коммерческой операции. Например, при покупке аннуитета за конкретную (известную) сумму с известными периодическими выплатами. В качестве примера рассмотрим аннуитет в размере 10 тыс. евро на 10-летний период. Если рассматриваемый аннуитет реализуется за 61450 евро, будет ли он для вас привлекательным с точки зрения ставки процента (эффективности) такой инвестиции?

Сразу отметим, что алгебраического решения уравнения относительно параметра r нет, и решение его отыскивается по табл. п. 2.1 (см. приложение 2).

Для этого сначала рассчитывается множитель дисконтирования (как отношение PV/ С), а затем по известным параметрам количества периодов аннуитета и множителя дисконтирования в таблице находится соответствующая им ставка процента. Для рассматриваемых выше условий r= 10%.

Определение стоимости срочного аннуитета

До сих пор мы исследовали аннуитеты с денежными потоками, возникающими в конце каждого периода, например в случае ссуды с ежемесячными по ней выплатами. Это так называемые простые, или обыкновенные, аннуитеты. Однако, когда вы, например, снимаете квартиру, арендная плата, как правило, уплачивается в начале каждого месяца, т.е. авансом. Такие аннуитеты носят название срочных, или авансовых. Рассмотрим, как оценивается срочный аннуитет, воспользовавшись схемой, иллюстрирующей соотношение срочного и простого аннуитетов (рис. 3.3).

Как следует из рисунка,

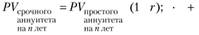
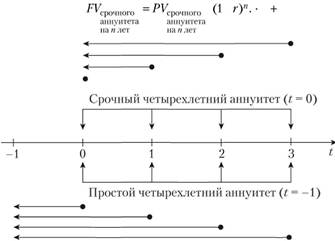
Рис. 3.3. Соотношение схем и способов расчета приведенной стоимости аннуитетов

Пример. Найдите приведенную и будущую стоимость срочного аннуитета сроком на 5 лет, под 8% годовых, с платежами в размере 5000 евро в год.

Решение.

Сначала необходимо определить приведенную стоимость эквивалентного простого аннуитета, используя выведенные ранее формулы:

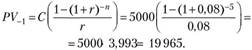
Так как нашли приведенную стоимость для t=-1, исчислим ее в момент :

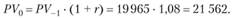
Теперь можно рассчитать будущую стоимость срочного аннуитета в :