и подход, основанный на изменении кредитных рейтингов
За последнее десятилетие появилось большое число новых систематических подходов к моделированию кредитного риска портфеля. Подход CreditMetrics, разработанный JP Morgan, ведущим американским банком, и впоследствии усовершенствованный RiskMetrics Inc., основывается на анализе изменения кредитного рейтинга. То есть подход основан на оценке того, насколько вероятно, что заемщик перейдет от одного кредитного качества к другому, включая дефолт в рамках определенного временно́го горизонта (обычно одного года).
Подход CreditMetrics позволяет банкам определить годовое будущее распределение стоимости (ценности) портфеля облигаций или займов, при котором изменения ценности связаны только с изменением кредитного рейтинга. (Будущие стоимости (ценности) и риски долговых инструментов в портфеле получены из детерминистических форвардных кривых процентных ставок.) Основным допущением подхода является то, что Назад история изменения рейтингов тысяч облигаций точно описывает переходные вероятности в следующем периоде.
Структура измерения риска CreditMetrics может рассматриваться в рамках двух основных строительных блоков.
1. Показатель VaR для кредитного риска, соответствующий кредиту по одному финансовому инструменту.
2. Показатель VaR для кредитного риска на уровне портфеля, который учитывает эффект диверсификации портфеля.
Эти строительные блоки внедряются в четыре этапа. Первым этапом данного подхода является определение системы рейтинга, уровней рейтинга и вероятностей перехода из одного кредитного качества в другое для определенного горизонта кредитного риска.
Вторым этапом является определение рискового горизонта, за который обычно принимается один год.
Третий этап – определение форвардной кривой ставок дисконтирования для заданного горизонта каждой рейтинговой категории. Это позволит нам оценить стоимость (ценность) облигации, используя бескупонную кривую доходности, соответствующую потенциальным будущим кредитным рейтингам эмитента. В случае дефолта стоимость (ценность) инструмента должна определяться с учетом уровня взыскания, который представляется как процент номинальной или нарицательной стоимости (ценности).
На четвертом (последнем) этапе объединяется информация, полученная на первых трех этапах, и рассчитывается будущее распределение изменений стоимости (ценности) портфеля вследствие изменения кредитного рейтинга.
Ключевой проблемой во всем этом является оценка переходных вероятностей или их матрицы с использованием исторических данных уровня дефолта из внешней или внутренней системы рейтингов (табл. 11-1).
Давайте рассмотрим подход, основанный на системе рейтингов и данных S&P, которая использует семь основных категорий рейтинга. Наивысший кредитный рейтинг – ААА; самый низкий – ССС. (Рейтинговые агентства применяют также более точную статистику, в которой каждая категория рейтинга от АА до СС разделяется на три подкатегории, например категория рейтинга S&P А делится на А+, А и А-.) Дефолт определяется как ситуация, при которой должник не может осуществить выплату, связанную с облигацией или кредиту, независимо от того, является ли выплата купонной (процентной) или выплатой основной суммы при погашении.
Для примера мы рассмотрим эмитента облигаций с текущим рейтингом ВВВ. Выделенная строка в табл. 11-1 показывает определенные S&P вероятности того, что кредитный рейтинг этого эмитента с рейтингом ВВВ будет меняться в течение одного года на одно из восьми возможных состояний, включая дефолт. Наиболее вероятна ситуация, что должник останется в той же категорию рейтинга, т.е. ВВВ; вероятность этого равна 86,93 %. Вероятность дефолта эмитента в течение одного года составляет только 0,18 %, а вероятность повышения рейтинга до ААА также очень низкая, т.е. 0,02 %.
Матрицы переходных вероятностей, аналогичные этой, разрабатываются рейтинговыми агентствами для всех первоначальных рейтингов на основе истории кредитных событий, имевших место в компаниях, которым присвоили рейтинг эти агентства (Мудиз публикует аналогичную информацию). Переходные вероятности, опубликованные агентствами, основываются на данных всех отраслей более чем за 20 лет. Очевидно, что эти данные необходимо рассматривать внимательно, так как они являются усредненными статистическими данными неоднородной выборки компаний на протяжении нескольких деловых циклов. Но этой причине многие банки предпочитают использовать собственную статистику, которая более точно отражает структуру их портфелей кредитов и облигаций.
ТАБЛИЦА 11-1
Матрица переходных вероятностей: вероятность изменения кредитного рейтинга в течение одного года
|
Первоначальный рейтинг |
Рейтинг к концу года, % |
|||||||
|
ААА |
АА |
А |
ВВВ |
ВВ |
В |
ССС |
Дефолт |
|
|
ААА |
90,81 |
8,33 |
0,68 |
0,06 |
0,12 |
0 |
0 |
0 |
|
АА |
0,70 |
90,65 |
7,79 |
0,64 |
0,06 |
0,14 |
0,02 |
0 |
|
А |
0,09 |
2,27 |
91,05 |
5,52 |
0,74 |
0,26 |
0,01 |
0,06 |
|
ВВВ |
0,02 |
0,33 |
5,95 |
86,93 |
5,30 |
1,17 |
0,12 |
0,18 |
|
ВВ |
0,03 |
0,14 |
0,67 |
7,73 |
80,53 |
8,84 |
1,00 |
1,06 |
|
В |
0 |
0,11 |
0,24 |
0,43 |
6,48 |
83,46 |
4,07 |
5,20 |
|
ССС |
0,22 |
0 |
0,22 |
1,30 |
2,38 |
11,24 |
64,86 |
19,79 |
Источник: Standart & Poot's, CreditWeek, April 15,1996.
Рейтинговые агентства обычно присваивают рейтинг заемщику "с учетом цикла" (through-the-cycle, ТТС). Иными словами, рейтинговые агентства снижают стандартное влияние делового цикла на должника, так как они считают, что структурная оценка кредитного риска должника на протяжении цикла не меняется. И наоборот, специалисты по аналитическому моделированию (например, подход KMV, который будет описан позднее) обычно присваивают рейтин г на основе подхода "момент времени" (point-in-time, PIT) и, следовательно, их рейтинг более точно отражает вероятность дефолта в краткосрочной перспективе. Банку, внедряющему внутреннюю систему рейтингов, необходимо решить, должны ли статистические данные по рейтингу и соответствующей вероятности дефолта основываться на подходе с учетом цикла или момента времени. Если банк решает использовать подход момента времени, то волатильность рейтингов и, следовательно, показатель VaR дня кредитного риска и экономический капитал будут выше, чем при использовании подхода с учетом цикла.
Реализованные переходные вероятности и вероятности дефолта с течением времени существенно колеблются по годам в зависимости от состояния экономики (спад или подъем) (см. рис. 11-2). При внедрении модели, которая основывается на переходных вероятностях перехода, банку, возможно, будет необходимо скорректировать средние исторические значения (см. табл. 11-1) для соответствия оценке текущей экономической среды. Вероятности в диагональных ячейках матрицы переходных вероятностей для подхода "момент времени" ниже, чем вероятности для подхода с учетом цикла, поскольку для первого подхода вероятность того, что рейтинг не изменится в последующие периоды, ниже.
Следующим шагом в создании распределения стоимостей (ценностей) отдельной облигации является определение стоимости (ценности) облигации для каждого из семи возможных кредитных рейтингов. Для этого нам необходимо определить семь возможных годовых форвардных бескупонных кривых так, чтобы облигацию можно было оценить на всех возможных этапах. Эти кривые можно получить на основании рыночных данных, используя цены облигации, что отражено в табл. 11-2. (Форвардные бескупонные кривые доходности отражают предполагаемую ставку дисконтирования для будущих денежных потоков, полученную с учетом текущей цены облигации для конкретного кредитного рейтинга и различных сроков погашения; см. гл. 6.) Мы не можем полагать, что стоимость облигации нулевая, если дефолт эмитента произойдет в конце года. В зависимости от приоритетности инструмента уровень возмещения долга в случае дефолта реализуется инвестором. Эти уровни снова определяются из исторических данных, представленных рейтинговыми агентствами. В табл. 11-3 показаны ожидаемые уровни возмещения долга в случае дефолта для различных классов облигаций, полученные компанией "Мудиз". Следовательно, при моделировании, осуществляемом для оценки распределения портфеля, уровни возмещения долга в случае дефолта не считаются фиксированными, а рассматриваются как полученные из распределения возможных уровней взыскания. (Как правило, уровень возмещения долга в случае дефолта банковского займа значительно выше, чем уровень возмещения долга в случае дефолта облигации.)
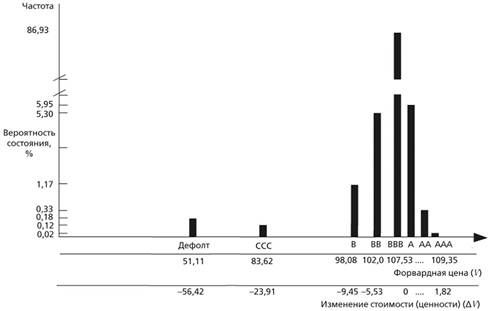
Теперь мы можем рассчитать распределение изменений стоимости (ценности) облигации для периода времени один год, которое является результатом последующего изменения кредитного качества. В табл. 11-4 и на рис. 11-3 показаны эти изменения для нашего примера с облигацией, имеющей рейтинг ВВВ.
Первый процентиль распределения, который соответствует показателю VaR для кредитного инструмента при доверительном уровне 99 % составляет 23,91. То есть мы можем сказать, что если портфель состоит из 100 неза-
ТАБЛИЦА 11-2
Годовые форвардные бескупонные кривые доходности для каждого кредитного рейтинга, %
|
Категория |
Год |
|||
|
1 |
2 |
3 |
4 |
|
|
AAA |
3,60 |
4,17 |
4,73 |
5,12 |
|
АА |
3,65 |
4,22 |
4,78 |
5,17 |
|
А |
3,72 |
4,32 |
4,93 |
5,32 |
|
ВВВ |
4,10 |
4,67 |
5,25 |
5,63 |
|
ВВ |
5,55 |
6,02 |
6,78 |
7,27 |
|
В |
6,05 |
7,02 |
8,03 |
8,525 |
|
ССС |
15,05 |
15,02 |
14,03 |
13,52 |
Источник: CreditMetrics, JP Morgan.
ТАБЛИЦА 11-3
Уровни возмешения долга в случае дефолта по степени приоритета (процент от номинальной стоимости (ценности), т.е. "номинала"]
|
Класс приоритета |
Среднее, % |
Среднеквадратическое отклонение, % |
|
Старшая обеспеченная |
53,80 |
26,86 |
|
Старшая необеспеченная |
51,13 |
25,45 |
|
Старшая субординированная |
38,52 |
23,81 |
|
Субординированная |
32,74 |
20,18 |
|
Младшая субординированная |
17,09 |
10,90 |
Источник: Carty and Lieberman (1996).
ТАБЛИЦА 11-4
Распределение ценности облигации и изменения стоимости (ценности) облигации с рейтингом ВВВ за один год
|
Рейтинг к концу года |
Вероятность состояния (/?), % |
Форвардная иена (V), ДОЛЛ. |
Изменение ценности [ΔΙΟ, ΔΟΛΛ. |
|
ААА |
0,02 |
109,35 |
1,82 |
|
АА |
0,33 |
109,17 |
1,64 |
|
А |
5,95 |
108,64 |
1,11 |
|
ВВВ |
86,93 |
107,53 |
0 |
|
ВВ |
5,30 |
102,00 |
-5,53 |
|
В |
1,17 |
98,08 |
-9,45 |
|
ссс |
0,12 |
83,62 |
-23,91 |
|
Дефолт |
0,18 |
51,11 |
-56,42 |
Источник: Credit Metrics, JP Morgan.
висимых заемщиков с рейтингом ВВВ, в этом случае за год можно ожидать, что один заемщик будет нести потери больше, чем 23,91.
Однако необходимо также отметить небольшую, но важную вероятность очень больших потерь в случае дефолта. Любой график распределения, построенный в виде столбиков на рис. 11-3, покажет то, что специалисты по моделированию называют "длинный хвост", который часто рассматривают как "тяжелый хвост" – типичное свойство распределений стоимости (ценности) кредита.
РИСУНОК 11-3. Гистограмма однолетних форвардных иен и изменений стоимости (ценности) облигации с рейтингом ВВВ